第3章　利潤函數

1．一個競爭性的利潤最大化廠商有利潤函數。將產出價格正規化，令其等于1。

（a）對函數求一階導數和二階導數，可以得到什么結論？

（b）如果是對要素的要素需求函數，的符號是什么？

（c）令為產生這種形式的利潤函數的生產函數。這種生產函數的形式是什么樣子的？（提示：參見一階條件）

A competitive profit-maximizing firm has a profit function .The price of output is normalized to be 1.

（a）What do we know about the first and second derivatives of the functions ?

（b）If  is the factor demand function for factor ， what is the sign of ?

（c）Let  be the production function?（Hint：look at the first-order conditions.）

答：（a）由利潤函數的凸性得到，從而可知；又因為利潤函數關于要素價格是單減的，即，從而可知。

（b）根據Hotelling引理可知，因此。

（c）由（b）可知，又因為對，恒成立。

從中反解出代入上式中可知只和有關；同理可知只和有關，從而可知一定可以寫成如下形式：。

2．考慮，和，所描述的技術。計算出這種技術的利潤函數。

　 Consider the technology described by  for and for . Calculate the profit function for this technology.

解：令，易知在區間上單增，在區間上單減，所以在這一點上達到最大值。下面分情況討論：

（1）當 時，如果廠商停產，那么它的利潤就是零；如果廠商繼續生產，那么當它的產量為1時，可以得到最高利潤為。所以，廠商的最優選擇就是不生產。

（2）當時，如果廠商停產，那么它的利潤就是零；如果廠商繼續生產，那么當它的產量為時，可以得到最高利潤，為。所以如果即時，廠商應當選擇生產數量的產品，相應的利潤為；如果，那么廠商應當選擇停產，此時的利潤為零。

綜上可知，廠商的利潤函數為：

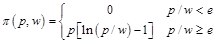
如圖3-1所示。

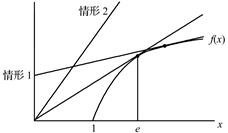
圖3-1　廠商的利潤最大化

3．給出生產函數，計算出利潤最大化的需求和供給函數，以及利潤函數。為簡單起見，假定存在內解。假定。

Given the production function ，calculate the profit-maximizing demand and supply functions，and the profit function. For simplicity assume an interior solution. Assume that .

解：利潤最大化問題：

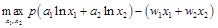
一階條件為：

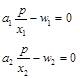
得出要素需求方程為：，。

將要素需求方程代入生產函數，得到供給函數：

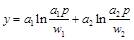
將要素需求方程代入目標函數就得出利潤函數：

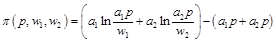
4．給出生產函數，計算出利潤最大化的需求和供給函數，以及利潤函數，假定。和

必須滿足什么樣的約束？

　  Given the production function ，calculate the profit-maximizing demand and supply functions, and the profit function. Assume . What restrictions must and  satisfy?

解：利潤最大化問題：

一階條件是：

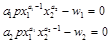
解得要素需求函數：

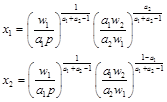
將要素需求函數代入目標函數即求得利潤函數:

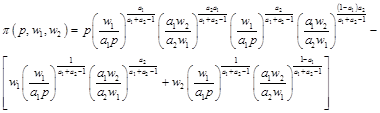
當時，生產函數規模報酬遞增，所以不存在最大利潤；當時，得到柯布—道格拉斯生產函數，所以不存在最大利潤；當時，優化問題的海賽矩陣負定，所以存在最大利潤。

綜上可知時，利潤最大化問題有解。

5．給出生產函數，計算出利潤最大化的需求和供給函數，以及利潤函數。必須滿足什么約束？

   Given the production function , calculate the profit -maximizing demand and supply functions, and the profit function. What restriction must a satisfy?

解：廠商的利潤最大化問題為：

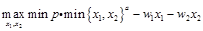
對于最優解必有，所以上述最優化問題可以化簡為：

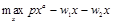
從而解得要素需求函數為：

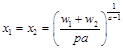
將要素需求函數代入生產函數得到供給函數：

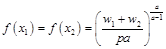
將要素需求函數代入目標函數得到利潤函數：

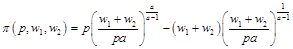
上述最優化問題的二階條件為，可見為了滿足二階條件必須有；當時，生產函數規模報酬遞增，所以不存在最大利潤；當時，只有當時，廠商有最大利潤（等于零），當時，廠商無最大利潤；綜上可知：當時，廠商的利潤函數處處存在。