3.1　復習筆記

一、概率

（一）概率

1．隨機現象

在自然界和社會生活中，存在著兩種不同類型的現象，即確定性現象和隨機現象。

（1）確定性現象

①含義

在一定的條件下事先可以斷言必然會發生某種結果的現象叫確定性現象。

②分類

a．必然現象，是指在一定條件下必然會發生的現象。

b．不可能現象，是指在一定的條件下必然不會發生的現象。

（2）隨機現象

①含義

隨機現象是指在一定條件下，事先不能斷言會出現哪種結果的現象。

②特點

a．具有偶然性

隨機現象具有偶然性，一次試驗前，不能預言發生哪一種結果。

b．具有必然性

在相同條件下，進行大量次重復試驗，呈現出統計規律性，這說明隨機現象也具有必然性。

③隨機事件

隨機現象中出現的各種可能的結果稱為隨機事件，簡稱為事件。隨機事件的極端情況包括：

a．必然事件，當某一事件包含隨機試驗中所有可能的結果，則稱這一事件為必然事件。

b．不可能事件，當某一事件不包含隨機試驗中的任何結果，則稱這一事件為不可能事件。

2．事件與概率

（1）事件

①頻率的穩定性

如果進行多次試驗和觀察，事件的出現情況就能體現出一定的規律性，這種規律性就是頻率的穩定性。頻率的穩定性說明隨機事件發生的可能性的大小是隨機事件本身所固有的，不隨人們意志改變的一種客觀屬性，可以對其進行度量。

②頻率的計算公式

在N次重復試驗中統計出事件A發生的次數n，并計算n與試驗總次數N的比值，這個比稱為事件A發生的頻率，記作F_N(A)

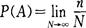
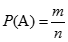
c．特點

事先就已經知道有關事件出現的事實，在試驗或研究之前，就能決定事件發生的概率。故又稱這種概率為先驗概率。

③統計定義與古典定義的概率具有的共同性質

a．必然事件發生的概率為1

b．不可能事件的概率為0；

c．事件A發生的概率滿足：；

d．逆事件的概率：。

④概率的兩個基本定理

a．概率的加法定理

若A、B是兩個互不相容的事件，則A和B至少有一個發生的概率為：

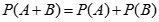
當有有限多個相互獨立事件的情況，則有：

若A1，A2，…，An是有限個相互獨立的事件，則A1，A2，…，An至少有一個發生的概率為：

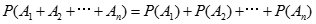
b．概率的乘法定理

若A、B是兩個相互獨立事件，則A和B同時發生的概率P(A·B)為：

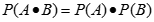
若A₁，A₂，…，A_n是有限個相互獨立事件，則A₁，A₂，…，A_n同時發生的概率為：

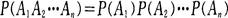
（二）二項式定理

1．排列與組合

（1）排列

①定義

從n個不同的元素中，任取m個（m≤n）元素，按一定的順序排成一列，稱為從n個不同元素中取出m個元素的一個排列。當m＜n時，所得排列稱為選排列，記作。當n=n時，所得排列稱全排列，記作。

②計算公式

　

　

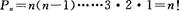
（2）組合

①定義

從n個不同元素中，任取m個（m≤n）元素，不管順序，并成一組，稱為從n個不同的元素中取出m個元素的一個組合，記作

②公式 

　

 

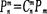
③組合的兩個性質

應用組合的計算公式，二項式定理可寫成：

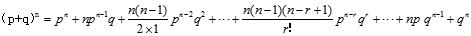
（2）的二項展開式的性質

①展開式共有n+1項；

②p按降冪排列，指數從n逐項減1到0；q按升冪排列，指數從0逐項增1到n；

③各項次數和等于二項式的次數；

④從第一項起，各項系數依次為：；

⑤由組合的性質（）知，由兩端起等距項的系數相等。

⑥當項數為奇數時（二項式的指數n為偶數）；中間一項的系數最大；當項數為偶數時（二項式的指數n為奇數），中間兩項的系數相等且最大。

（3）楊輝三角

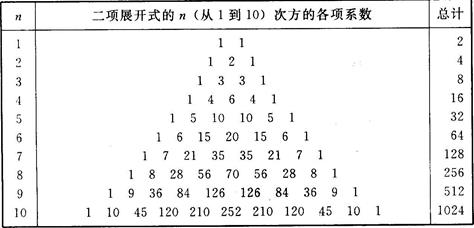
楊輝三角有助于記憶二項展開式各項系數的分配規律。在楊輝三角的表（如表3-1所示）中，可從中找到n（從1到10）次方的系數。注意：每行中的任何值均由它頂上左右兩個值相加而得。按這種方法可為更大的n值求得二項式的各項系數。它的優點在于能簡捷地確定二項展開式的各項系數。

表3-1  楊輝三角（n=10）

 

　 

　 

其中，n為二項試驗的總次數，p為事件發生的概率，。

三、正態分布

（一）正態分布

1．正態分布的密度函數

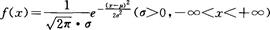
其中：π是圓周率；e是自然對數的底；x為隨機變量的取值；μ為正態分布的均值；σ²為正態分布的方差。正態分布一般記作。

2．正態曲線

（1）含義

正態曲線是指由正態分布密度函數f（x）的表達式繪出的正態分布密度函數的曲線，簡稱為正態曲線（如圖3-1所示）。

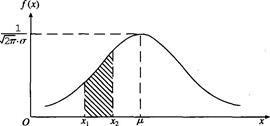
圖3-1  正態分布的密度函數曲線

（2）基本性質

①正態曲線位于x軸的上方，以直線x=μ為對稱軸，μ為正態分布的均值，它向左向右對稱地無限伸延，且以x軸為漸近線。

②當x=μ時，曲線處于最高點，為最大值；x=μ±σ兩點是拐點，當正態曲線由中央向兩側逐漸下降時，到拐點改變了彎曲方向，整條曲線呈現“中間高，兩邊低”的形狀。

③正態曲線與x軸所圍成區域的面積為1，將正態曲線分成面積均為0．5的兩部分。服從正態分布的隨機變量x在x₁到x₂間變化的概率(x₁≤x₂)就是x=x₁，x=x₂兩軸之間曲線下的面積。

④正態分布x～N（μ，σ²）是由均值μ和標準差σ唯一決定的分布。均值μ決定曲線的位置；標準差σ決定曲線的形狀。σ愈大，曲線愈“矮胖”，σ愈小，曲線愈“高瘦”。

（二）標準正態分布

1．定義

當均值為0，標準差為1時的正態分布稱為標準正態分布，記作N（0，1）。標準正態分布的密度函數為：

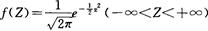
2．標準正態分布曲線（如圖3-2所示）

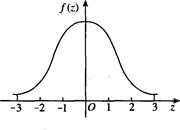
圖3-2  標準正態分布曲線

3．標準正態分布的性質

（1）標準正態分布的位置、形狀唯一確定。

（2）標準正態分布曲線在Z=0時達到最大值，密度函數為0.3989。

（3）曲線上Z=±1兩點為拐點，曲線呈現“中間高，兩邊低”的形狀。

（4）標準正態分布與一般正態分布可以轉換。

4．一般正態分布與標準正態分布的轉換

任何一般正態分布，都可以通過轉化為標準正態分布Z～N（0，1）。因為是線性轉化，轉換后正態分布的各項性質都保持不變。

（三）正態分布表的使用

1．正態分布表

正態分布表包括三列：

（1）第一列表示曲線底線即橫軸上的位置，用Z表示。對于正態分布x～N(μ，σ₂)而言，z值相當于

（2）第二列是縱高Y，即曲線的高度，對于某Z₀值縱高Y由計算。

（3）第三列是陰影部分的面積（如圖3-3所示），用P表示，即概率P。

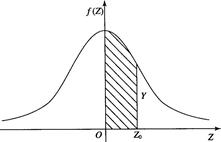
圖3-3  正態分布表中Z、Y、P的意義

2．使用正態分布表時需要注意的問題

（1）正態分布表只列出Z≥0。所對應的縱高和面積。當z≤0時，可根據正態曲線的對稱性，在正態分布表中查出-Z所對應的面積和縱高。

（2）對服從正態分布的變量x，先通過，轉化為Z值，即計算得到以標準差σ為單位的離均差后，才能查表。

3．正態分布表的用途

（1）已知和，求概率；

（2）由曲線下的面積P（概率）求Z值；

（3）由Z值或面積（概率）P，求縱高Y。

（四）正態分布的實際應用

1．標準分數

（1）含義

標準分數又稱Z分數，它以標準差為單位，反映了一個原始分數在團體中所處的位置。

（2）計算公式

①若已知一個總體，則這個總體中的原始分數的標準分數用下式計算：

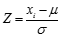
式中：Z為標準分數；為某個數據或分數；μ為總體平均數；σ為總體標準差。

②若僅已知一個待研究總體中的樣本，則在這個樣本中的原始分數的標準分數用下式計算：

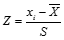
式中：Z為標準分數，為某個數據或分數，為樣本平均數，S為樣本標準差。

（3）性質

若原始分數服從(或近似服從)正態分布時，標準分數有如下的性質：

①由原始分數轉換得到的Z分數的平均數為0；

②由原始分數轉換得到的Z分數的標準差為1；

③當X是以μ為平均數，為方差的正態分布總體，則經過轉換后得到的標準分數所產生的新總體也為正態，且平均數為0，方差為l。

2．若考試成績服從正態分布，確定錄取分數線；

3．確定在正態分布下特定分數界限內的考生人數。