- 尼科爾森《微觀經濟理論—基本原理與擴展》(第9版)課后習題詳解
- 圣才電子書
- 3544字
- 2020-09-11 18:26:27
第5章 收入效應和替代效應
1.口渴的Ed僅喝純泉水,但是他可以購買0.75升或2升瓶裝的礦泉水。由于水本身是同質的,所以他將以上兩種瓶裝礦泉水視為完全替代品。
(1)假定Ed的效用僅取決于其消費的水量,而瓶子對他而言無任何效用,請將其效用函數表示為規格為0.75升( )和2升(
)和2升( )的瓶的數量的函數。
)的瓶的數量的函數。
(2)求出需求函數 。
。
(3)畫出 和
和 不變時,
不變時, 的需求曲線。
的需求曲線。
(4) 和
和 的變化如何影響
的變化如何影響 的需求曲線?
的需求曲線?
(5)在此情況下, 的補償需求曲線形狀是什么樣的?
的補償需求曲線形狀是什么樣的?
解:(1)Ed的效用函數可以表示為: 。
。
(2)由Ed的效用函數可知,他的偏好為完全替代型偏好,所以為了實現效用最大化,他將購買相對便宜的那種商品,由于無差異曲線斜率為 ,預算約束線斜率為
,預算約束線斜率為 ,即:
,即:
當 時,即
時,即 時,
時, ,
, ;
;
當 時,即
時,即 時,
時, ,
, ;
;
(3) 的需求曲線如圖5-1所示。
的需求曲線如圖5-1所示。
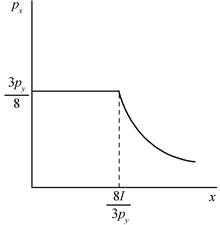
圖5-1  的需求曲線
的需求曲線
(4)收入 的提高將使
的提高將使 的需求曲線向右上方移動。商品
的需求曲線向右上方移動。商品 的價格降低將不會影響
的價格降低將不會影響 的需求,直到
的需求,直到 時為止。當
時為止。當 時,商品
時,商品 的需求減至0。
的需求減至0。
(5) 的收入補償需求曲線表示成當前消費的一個單點
的收入補償需求曲線表示成當前消費的一個單點 。假定
。假定 ,則
,則 的任何變化都會改變從該點處所得的效用。
的任何變化都會改變從該點處所得的效用。
2.戴維每周有3美元可供自由支配。他只喜歡花生醬和果凍三明治,因此他將所有貨幣都花費在花生醬(每盎司0.05美元)與果凍(每盎司0.10美元)上。面包則由一位熱心的鄰居免費提供。戴維偏好自己的吃法,嚴格按1盎司果凍2盎司花生醬的比例配置三明治,從不改變配方。
(1)戴維一周中用3美元購買花生醬與果凍各多少?
(2)如果果凍價格上升至每盎司0.15美元,他購買花生醬與果凍各多少?
(3)在(2)中,果凍價格上漲后,戴維的可支配收入應該增加多少才能補償價格上漲?
(4)圖示(1)到(3)的結論。
(5)在何種意義下,這個問題僅包括花生醬或果凍三明治一種商品?圖示這種單一商品的需求曲線。
(6)根據對果凍需求的替代效應與收入效應來討論這一問題的結論。
解:(1)由題可知,戴維的偏好是互補型的偏好。假設花生醬的消費量為 ,果凍三明治的消費量為
,果凍三明治的消費量為 ,則戴維的效用函數可以表示為:
,則戴維的效用函數可以表示為: 。
。
因此,效用最大化要求: ;此外,預算約束為:
;此外,預算約束為: 。
。
因而可以解得: ,
, 。
。
(2)如果果凍的價格增至每盎司0.15美元,則戴維的預算約束變為: ;結合效用最大化條件
;結合效用最大化條件 ,可知:
,可知: ,
, 。
。
(3)為了在價格上漲后繼續消費 ,
, ,戴維需要多購買6盎司的花生醬和3盎司的果凍三明治,這要求收入增加:
,戴維需要多購買6盎司的花生醬和3盎司的果凍三明治,這要求收入增加: (美元)。
(美元)。
(4)(1)到(3)的結論如圖5-2所示。
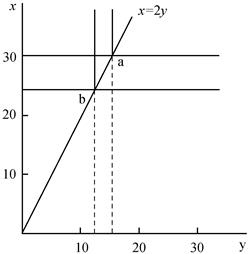
圖5-2 互補型偏好下價格變化的影響
(5)因為戴維僅按固定的比例使用花生醬和果凍,而且面包是免費的,所以,可以將此問題視為他以價格
 來購買三明治。
來購買三明治。
在(1)問中, ,花生醬—果凍三明治的數量為:
,花生醬—果凍三明治的數量為: ;
;
在(2)問中, ,花生醬—果凍三明治的數量為:
,花生醬—果凍三明治的數量為: 。
。
一般而言,花生醬—果凍三明治這種單一商品的需求曲線為: ,是一條雙曲線。
,是一條雙曲線。
(6)對于固定比例的效用函數而言,不存在替代效應,價格的變化僅導致收入效應。
3.如果任意一條從原點出發的直線通過所有的無差異曲線斜率相等的點,即 取決于
取決于 的點,那么效用函數是位似的。
的點,那么效用函數是位似的。
(1)證明:在這種情況下, 是常數。
是常數。
(2)證明:如果個人偏好可以用位似的無差異曲線圖來表示,則價格與數量必定按相反方向變化,即不會產生吉芬悖論。
證明:(1)隨著收入的增加, 的比值保持不變,效用最大化條件要求
的比值保持不變,效用最大化條件要求 也保持不變。而
也保持不變。而 取決于
取決于 ,從而
,從而 也必須保持不變。又因為收入僅用于購買
也必須保持不變。又因為收入僅用于購買 和
和 ,所以
,所以 和
和 都與收入成比例,即有
都與收入成比例,即有 是常數。
是常數。
(2)由(1)可知, ,
, ,這說明
,這說明 ,
, 兩種商品都是正常物品,而吉芬品為劣等品,所以吉芬悖論不成立。
兩種商品都是正常物品,而吉芬品為劣等品,所以吉芬悖論不成立。
4.假設效用由下式給出:
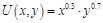
(1)用非補償需求函數計算間接效用函數與支出函數。
(2)用(1)中計算出的支出函數與Shephard引理計算 的補償需求函數。
的補償需求函數。
(3)用(2)中得出的結論與 商品的非補償需求函數證明本題符合斯勒茨基方程式。
商品的非補償需求函數證明本題符合斯勒茨基方程式。
解:(1)由柯布-道格拉斯效用函數的性質可得:
 ,
,
從而可得間接效用函數為:
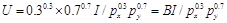
其中, 。
。
根據對偶性質,支出函數為: 。
。
(2)利用Shephard引理可知,補償需求函數為: 。
。
(3)因為: ,
, ,
, ,
, ,所以可得:
,所以可得:
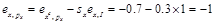
故本題符合斯勒茨基方程式。
5.假設 與
與 商品的效用函數為:
商品的效用函數為:
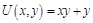
(1)計算 與
與 的非補償(馬歇爾)需求函數,并描述
的非補償(馬歇爾)需求函數,并描述 或其他商品的價格變化怎樣使
或其他商品的價格變化怎樣使 與
與 的需求曲線發生變化。
的需求曲線發生變化。
(2)計算 與
與 的支出函數。
的支出函數。
(3)用(2)中計算出的支出函數計算 與
與 商品的補償需求函數。描述當收入或其他商品價格發生變化時,
商品的補償需求函數。描述當收入或其他商品價格發生變化時, 與
與 的補償需求函數將如何發生變化。
的補償需求函數將如何發生變化。
解:(1)效用最大化問題為:
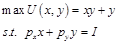
設拉格朗日函數為:
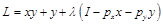
一階條件為:
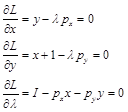
從而可以解得馬歇爾需求函數為:
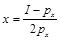
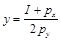
因此, 的變化不影響
的變化不影響 ,而
,而 的變化影響
的變化影響 。收入
。收入 的增加將使
的增加將使 與
與 的需求都增加,從而需求曲線向右上方移動。
的需求都增加,從而需求曲線向右上方移動。
(2)將 與
與 的需求函數代入效用函數,可得間接效用函數為:
的需求函數代入效用函數,可得間接效用函數為: ;
;
從而可以解得支出函數為: 。
。
(3)補償需求函數為:
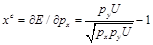
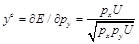
 的補償需求依賴于
的補償需求依賴于 ,而非補償需求不依賴于
,而非補償需求不依賴于 。收入的變化對補償需求沒有影響。
。收入的變化對補償需求沒有影響。
6.需求理論中的許多經驗研究工作主要集中于收入份額。對于任何商品 ,其收入份額定義為:
,其收入份額定義為: 。在本問題中,我們將證明大多數需求彈性可以從相應的份額彈性中求得。
。在本問題中,我們將證明大多數需求彈性可以從相應的份額彈性中求得。
(1)證明:某商品的預算份額關于收入的彈性 等于
等于 。請用一些數值例子來解釋這一結論。
。請用一些數值例子來解釋這一結論。
(2)證明:某商品的預算份額關于其自身價格的彈性 等于
等于 。請用一些數值例子來解釋這一結論。
。請用一些數值例子來解釋這一結論。
(3)利用你在(2)中所得的結論證明:商品 關于自身價格的支出彈性
關于自身價格的支出彈性 等于
等于 。
。
(4)證明:某商品的預算份額關于其他商品價格的彈性 等于
等于 。
。
(5)在第4章的擴展部分,我們已經證明了對于CES效用函數而言,商品 的支出份額為
的支出份額為 ,其中
,其中 。
。
利用此方程來證明方程: 。
。
提示:此問題可以通過假定 ,從而
,從而 來簡化。
來簡化。
證明:(1)由商品收入份額函數 ,可得:
,可得:
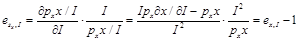
故如果 ,則
,則 。
。
(2)由商品收入份額函數 ,可得:
,可得:
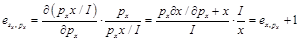
如果 ,則
,則 。
。
(3)因為在(2)中收入在求導時可以被消去,所以有: 。
。
(4)由商品收入份額函數 ,可得:
,可得:
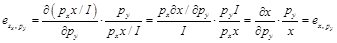
(5)由(2)可得:
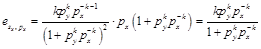
為了簡化,令 ,從而有:
,從而有: 。
。
再利用斯拉茨基方程,以及 ,可得:
,可得:
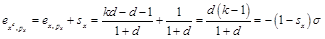
7.假定某人將漢堡包和奶酪視為完全互補品:他(或她)總是用一片漢堡包和一片奶酪做成一個漢堡包—奶酪三明治。同時假定此人僅購買漢堡包和奶酪這兩種商品,且面包是免費的。證明:
(1)如果漢堡包的價格等于奶酪的價格,則漢堡包需求的自身價格彈性是-0.5;漢堡包關于奶酪價格的交叉價格彈性也是-0.5。
(2)解釋為什么(1)中的結果僅反映收入效應,而不是替代效應。此問題中的補償價格彈性是多少?
(3)利用(2)中的結果說明:如果一片漢堡包的價格是一片奶酪價格的兩倍,則(1)問的答案將如何改變?
(4)解釋此問題可以通過假定此人僅消費一種商品——漢堡包—奶酪三明治來求解。
解:(1)漢堡包的消費量用 表示,奶酪的消費量用
表示,奶酪的消費量用 表示,因為漢堡包和奶酪是按照固定比例消費的,所以效用函數為:
表示,因為漢堡包和奶酪是按照固定比例消費的,所以效用函數為: ,因而漢堡包的需求為:
,因而漢堡包的需求為:
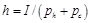
其中, 為收入,
為收入, ,
, 分別為漢堡包和奶酪的價格。
分別為漢堡包和奶酪的價格。
漢堡包需求的自身價格彈性為:
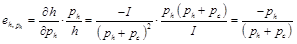
漢堡包關于奶酪價格的交叉價格彈性為:
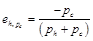
所以,當 時,
時, 。
。
(2)在固定比例效用函數下,不存在替代效應。補償價格彈性為0,由斯勒茨基方程可知: 。
。
(3)當 時,由(1)可知:
時,由(1)可知: ,
, 。
。
(4)如果此人僅消費漢堡包—奶酪三明治,則它們的需求的價格彈性為-1。該復合商品的價格彈性反映了整個三明治價格變化時漢堡包和奶酪的價格之間將成比例變化。例如,在(1)問中,漢堡包價格上漲10%,將導致三明治的價格上漲5%,從而導致需求數量下降5%。
8.證明:
(1)在柯布-道格拉斯效用函數情形下( ),商品
),商品 和
和 之間的價格彈性之間的關系為:
之間的價格彈性之間的關系為: 。
。
(2)如果 ,則
,則 ;如果
;如果 ,則
,則 。對此結論提供一個直觀的解釋。
。對此結論提供一個直觀的解釋。
(3)你如何將此結論推廣到更多商品的情形?討論這樣的推廣是否極其有意義。
答:(1)在柯布-道格拉斯效用函數情形下,價格彈性分別為:
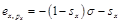
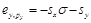
從而有: 。
。
(2)本題所欲證的結論可以由(1)問中的結論直接得到。直觀上,當 大時,價格彈性將大;當
大時,價格彈性將大;當 小時,價格彈性將小。
小時,價格彈性將小。
(3)對于多變量CES函數而言,該結論的推廣是可行的,但是該函數對行為施加的約束卻有可能不成立。
9.假定存在 種商品,商品
種商品,商品 的收入份額為
的收入份額為 。同時,我們定義如下彈性:
。同時,我們定義如下彈性:
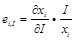
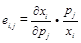
利用這些標記來證明:
(1)齊次性: ;
;
(2)恩格爾加總性: ;
;
(3)古諾加總性: 。
。
證明:(1)由于任何商品的需求關于價格都是零次齊次的,所以歐拉定理意味著:
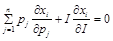
兩邊乘以 可得:
可得: ,又因為
,又因為 ,
, ,所以:
,所以:
(2)由預算約束 對收入
對收入 求導可得:
求導可得:
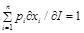
兩端乘以 可得:
可得: 。
。
(3)由預算約束 對
對 求導可得:
求導可得:
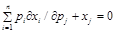
兩端乘以 可得:
可得: 。
。
10.某人在三年中的消費行為如表5-1所示:
表5-1

該行為是否與顯示偏好強公理相一致?
答:該行為違背了顯示偏好強公理。其理由如下:
第二年的消費束顯示偏好于第一年的消費束,因為在第二年的價格下,第一年和第二年的消費束的總支出是相同的。
第二年的消費束也顯示偏好于第三年的消費束,因為在第二年的價格下,第二年和第三年消費束的總支出是相同的。
但是在第三年的價格下,第二年的消費束的支出小于第三年的消費束的支出,而第二年的消費束卻沒有被選擇,因而這違背了顯示偏好強公理。