第四節 金融資產定價

考點七 利率與金融資產定價

（一）債券定價

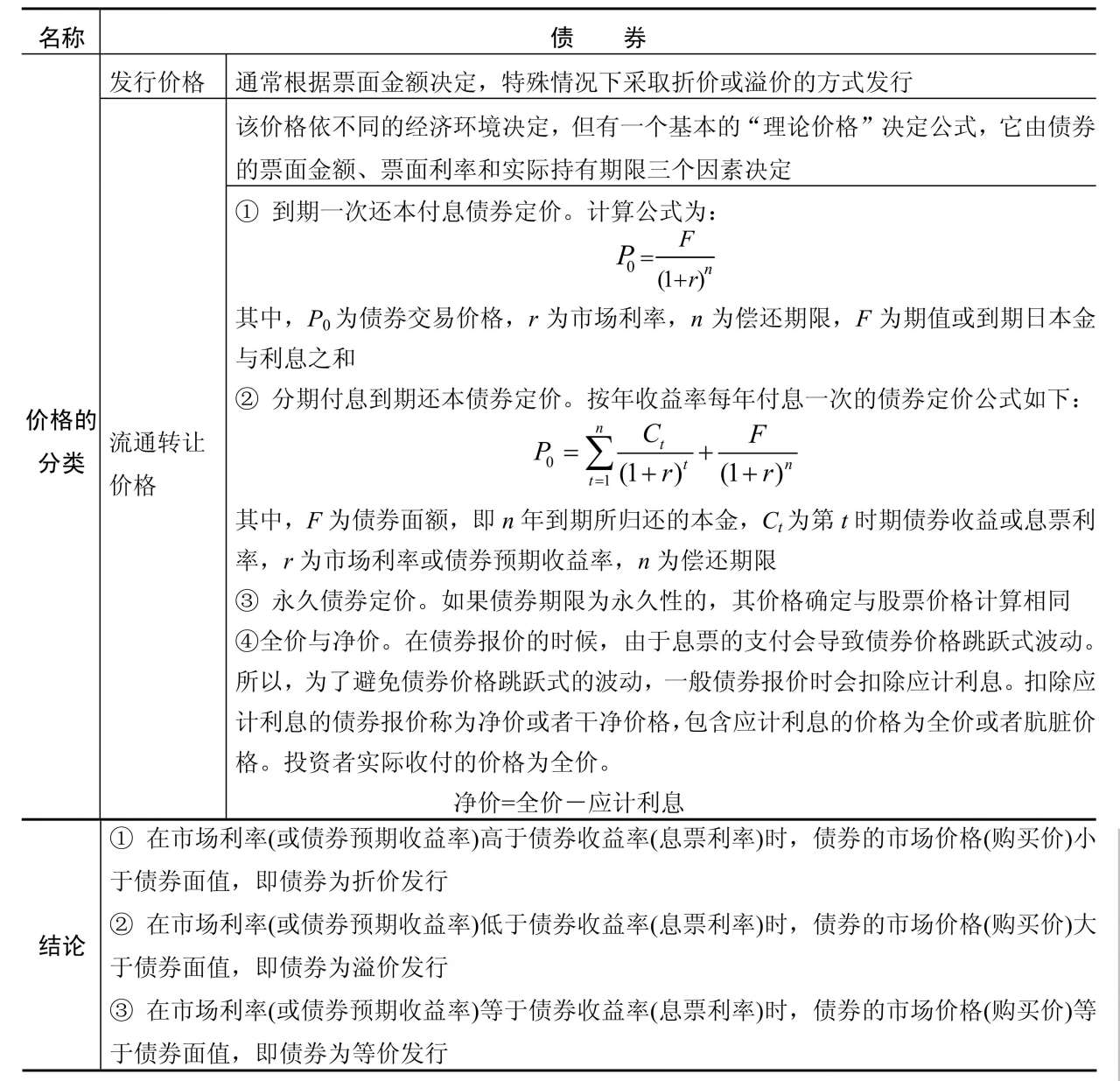
有價證券交易價格主要依據貨幣的時間價值，即未來收益的現值確定。利率與證券的價格成反比關系。這一關系適用于所有的債券工具。債券的定價方法見表2-7。

（二）股票定價

股票的價格由其預期收入和當時的市場利率兩個因素決定，其公式為：

股票的價格=預期股息收入/市場利率

股票靜態價格與動態價格的確定見表2-8。

考點八 資產定價理論

（一）有效市場假說

尤金·法瑪的有效市場假設奠定了對資產價值的認知基礎。該假說認為，相關的信息如果不受扭曲且在證券價格中得到充分反映，市場就是有效的。

當信息集從最小的信息集依次擴展到最大的信息集時，資本市場也就相應地從弱式有效市場逐步過渡到強式有效市場，見表2-9。

（二）資本資產定價理論及其假設條件

現代資產組合理論基于馬科維茨（1952）的研究，在這一理論中，對于一個資產組合，應主要關注其期望收益率與資產組合的價格波動率，即方差或標準差。投資者偏好具有高的期望收益率與低的價格波動率的資產組合。相等收益率的情況下優先選擇低波動率組合，相等波動率情況下優先選擇高收益率組合。資產組合的風險由構成組合的資產自身的波動率、方差、與資產之間的聯動關系和協方差決定。

資本資產定價模型假定：第一，投資者根據投資組合在單一投資期內的預期收益率和標準差來評價其投資組合；第二，投資者總是追求投資者效用的最大化，當面臨其他條件相同的兩種選擇時，將選擇收益最大化那一種；第三，投資者是厭惡風險的，當面臨其他條件相同的兩種選擇時，他們將選擇具有較小標準差的那一種；第四，市場上存在一種無風險資產，投資者可以按無風險利率借進或借出任意數額的無風險資產；第五，稅收和交易費用均忽略不計。

【例2-16】 馬科維茨認為在同一期望收益前提下，最為有效的投資組合（）。（2012年單選題）

A． 實際收益高

B． 實際收益低

C． 風險較高

D． 風險最小

【解析】D 美國經濟學家馬科維茨在1952年提出了均值—方差分析方法，為資本資產定價理論（CAPM）奠定了理論框架。馬科維茨認為在同一風險水平前提下，高收益率的投資組合最為有效；在同一期望收益前提下，低風險的投資組合最為有效。

1．資本市場線

資本市場線（CML），就是在預期收益率E（r）和標準差σ組成的坐標系中，將無風險資產（以rf表示）和市場組合M相連所形成的射線。所謂市場組合是指由所有證券構成的組合，在這個組合中，每一種證券的構成比例等于該證券的相對市值。資本市場線上的每一點都對應著某種由無風險資產和市場組合M構成的新組合。

資本市場線（CML）表示對所有投資者而言是最好的風險收益組合。任何不利用全市場組合或者不進行無風險借貸的其他投資組合都位于資本市場線的下方。

資本市場線（CML）的公式為：

2．證券市場線

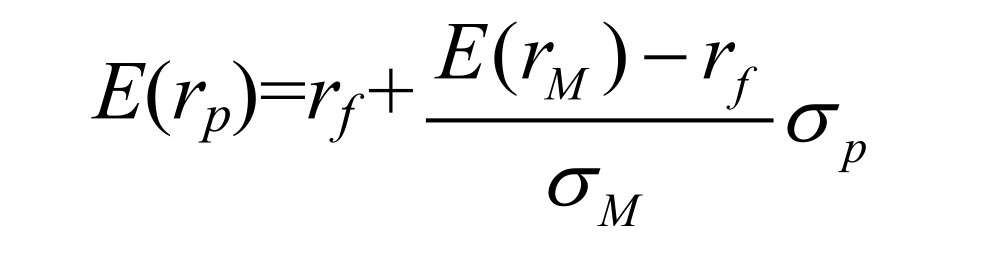
證券市場線是在資本市場線的基礎上，進一步說明了單個風險資產的收益與風險之間的關系。在考慮市場組合的風險時，重要的不是各種證券自身的整體風險，而是其與市場組合的協方差。由于市場組合的預期收益率E（rM）是各種證券預期收益率E（ri）的加權平均數，市場組合的標準差σM是各種證券與全市場組合的協方差σiM的加權平均數的平方根，其權數都等于各種證券在全市場組合中的比例。因此，我們可以得出如下結論：單個證券的預期收益率水平應取決于其與市場組合的協方差。

在均衡狀態下，單個證券風險和收益的關系可以寫為：

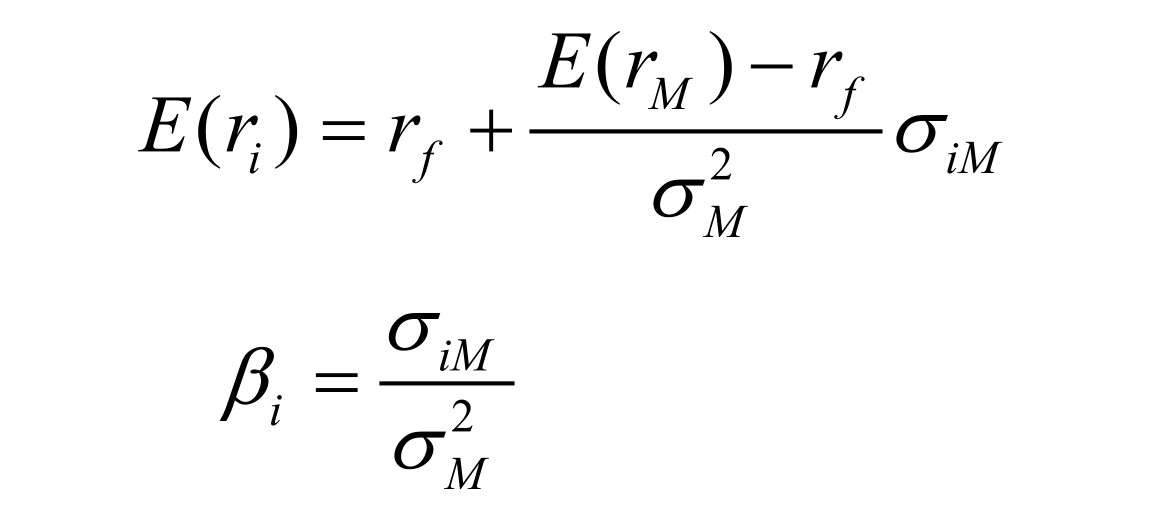
【例2-17】 如果某證券的β值為1.5，若市場投資組合的風險溢價水平為10%，則該證券的風險溢價水平為（）。（2012年單選題）

A. 5%

B. 15%

C. 50%

D. 85%

【解析】B 證券市場線的表達式E（ri）=rf+[E（rM）-rf]× βi，其中[E（rM）-rf]是證券的風險溢價水平，即市場投資組合的風險溢價水平。所以，該證券的風險溢價水平=1.5×10%=15%。

3．系統風險和非系統風險

資產風險一般有系統性風險和非系統性風險兩類。

（1）系統性風險是由宏觀經濟營運狀況或市場結構所引致的風險，又稱市場風險。它在市場上永遠存在，不可能通過資產組合來消除。資產定價模型（CAPM）研究不可消除系統性風險的指標，即風險系數β。

β 值還提供了一個衡量證券的實際收益率對市場投資組合的實際收益率的敏感度的比例指標。β值高（大于1）的證券被稱為“激進型”證券，這是因為它們的收益率趨向于放大全市場的收益率；β值低（小于1）的證券被稱為“防衛型”證券；而β值為1的證券被稱為具有“平均風險”的證券。

（2）非系統性風險是指具體的經濟單位自身投資方式所引致的風險，又稱特有風險。它可由不同的資產組合予以降低或消除，屬于可分散風險。

（三）期權定價理論

期權價值的決定因素主要有執行價格、期權期限、標的資產的風險度及無風險市場利率等。

1．布萊克—斯科爾斯模型的基本假定

該模型成立的假設條件包括下面幾條：

（1）無風險利率r為常數；

（2）沒有交易成本、稅收和賣空限制，不存在無風險套利機會；

（3）標的資產在期權到期時間之前不支付股息和紅利；

（4）市場交易是連續的，不存在跳躍式或間斷式變化；

（5）標的資產價格波動率為常數；

（6）假定標的資產價格遵從幾何布朗運動。

2．布萊克—斯科爾斯模型

根據布萊克—斯科爾斯模型，如果股票價格變化遵從幾何布朗運動，那么歐式看漲期權的價格C為：

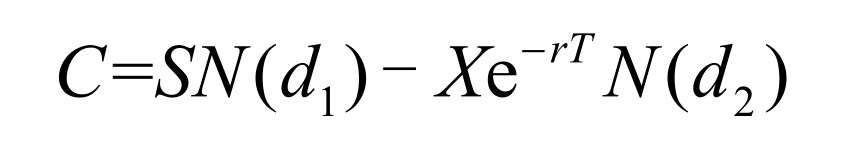
其中：

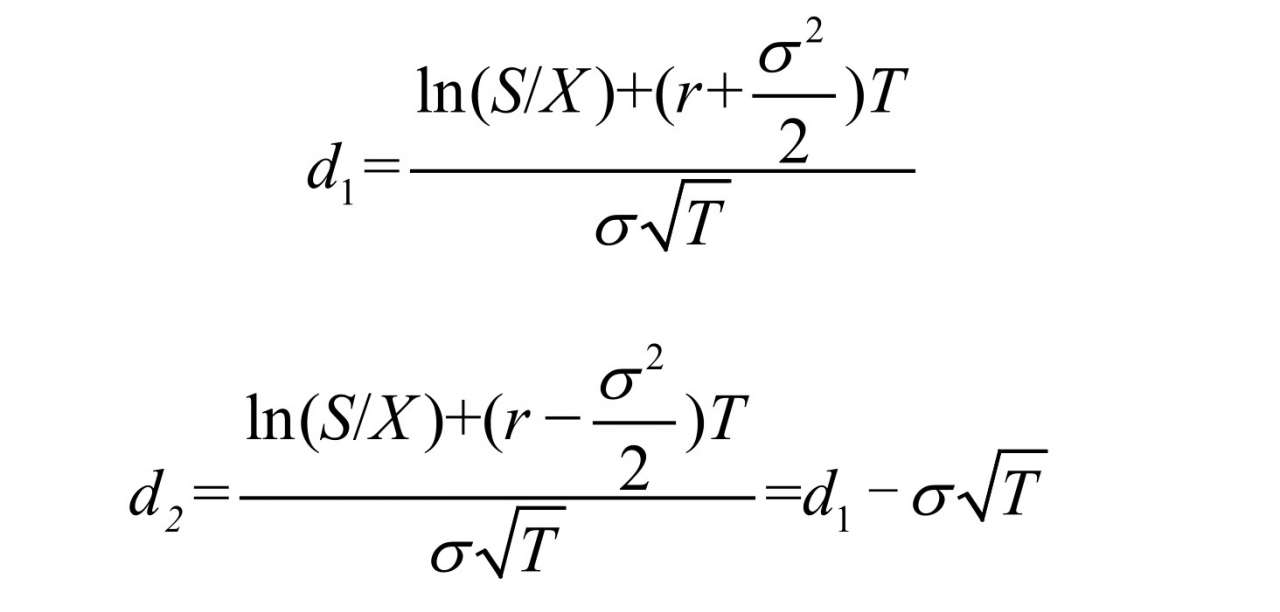
式中，S 為股票價格，X 為期權的執行價格，T 為期權期限，r 為無風險利率，e為自然對數的底（2.71828）, σ為股票價格波動率，N（d1）和N（d2）為d1和d2標準正態分布的累積概率。