2.7 行列式
行列式是指經過變換后的向量所構成的圖形的面積,與標準平面直角坐標系的基向量所構成的單位面積的比值,用det表示,例如二維矩陣A的向量對應的行列式表示為det(A)。顯然,在標準平面直角坐標系中,單位面積是1,其他矩陣的向量構成的圖形的面積是單位面積1的倍數,也就是結果數值本身。如下所示的矩陣的行列式結果表示為了e。
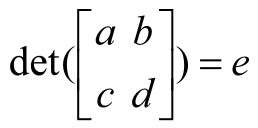
假設有如下矩陣:
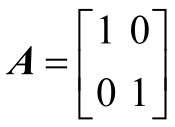
矩陣的長寬都是單位長度1,在坐標系中的表示如圖2-12所示。
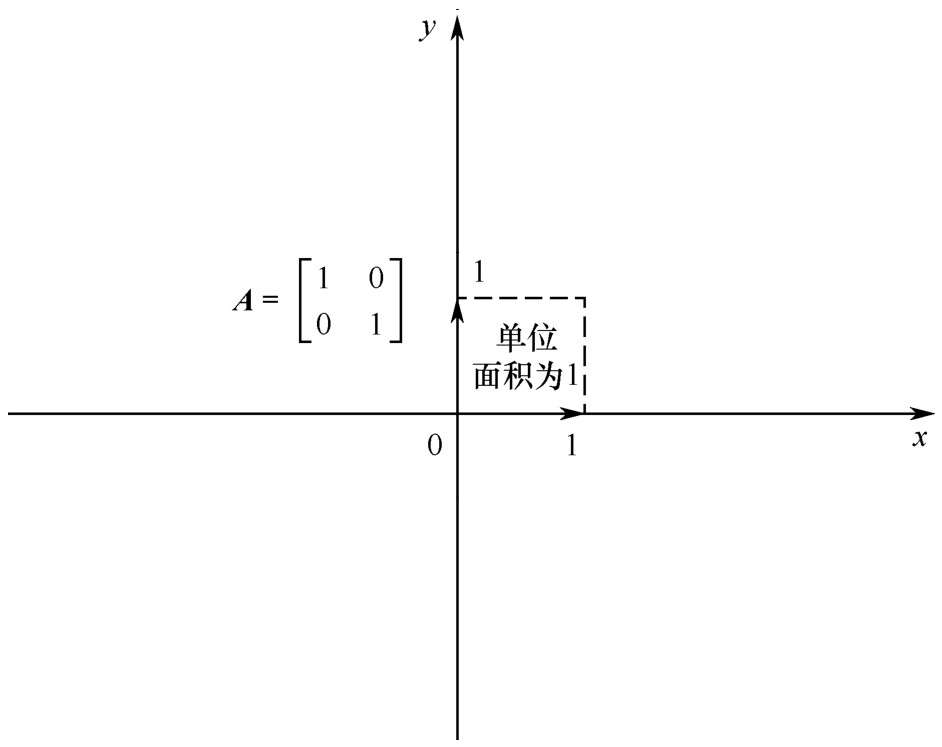
圖2-12 長寬都是1的矩陣
所以我們能以如下方式來表示該矩陣:
det( A)=1
現在來看另一個例子,假設有矩陣:
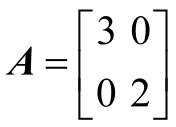
矩陣的長度為3,寬度為2,在坐標系中的表示如圖2-13所示:
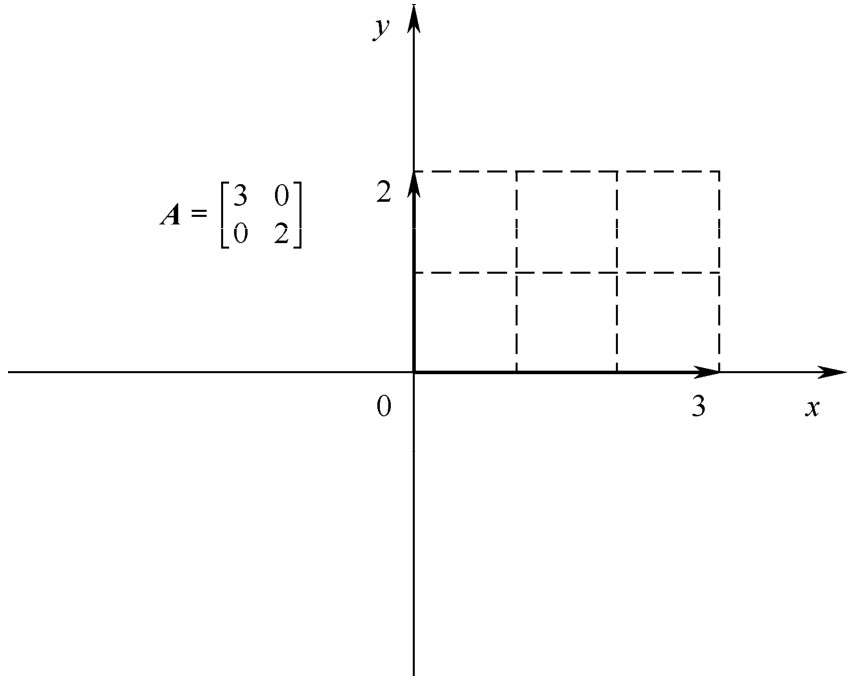
圖2-13 長3寬2的矩陣
我們可以以如下方式表示該矩陣:
det ( A)=6
此外,行列式可以為負值,當為負值時,空間坐標系的方向就變了,簡單講就是坐標系翻轉了。行列式符合下面的法則:
det (M1M2 )=det(M 1 )(M 2 )
推薦閱讀
- 亮劍.NET:.NET深入體驗與實戰精要
- 空間機器人遙操作系統及控制
- 精通Windows Vista必讀
- 程序設計語言與編譯
- 計算機圖形圖像處理:Photoshop CS3
- 最后一個人類
- PostgreSQL Administration Essentials
- DevOps:Continuous Delivery,Integration,and Deployment with DevOps
- 人工智能實踐錄
- 中國戰略性新興產業研究與發展·工業機器人
- Ruby on Rails敏捷開發最佳實踐
- JRuby語言實戰技術
- 渲染王3ds Max三維特效動畫技術
- PostgreSQL High Performance Cookbook
- 軟件測試設計