- 移動深度學習
- 李永會
- 373字
- 2019-12-05 14:22:37
2.1.1 標準平面直角坐標系
在了解矩陣和線性變換之前,我們先回顧一下二維(平面)坐標系,這有助于我們理解更復雜的概念。初中幾何中最常見的坐標系就是由法國數學家笛卡兒創建的標準平面直角坐標系,如圖2-1所示。
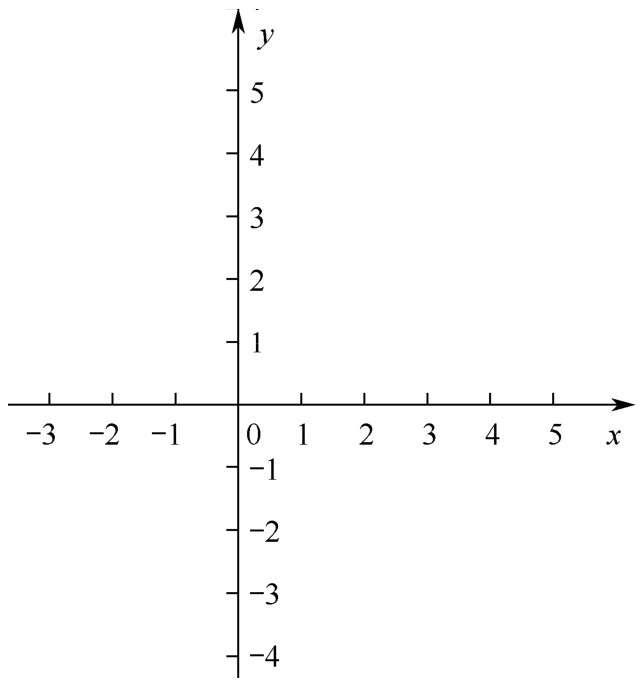
圖2-1 標準平面直角坐標系
平面直角坐標系中的任意一個向量都可以由最基本的向量 和
和 來表示,我們將這兩個向量稱為基向量(也叫基底、基),如圖2-2所示。
來表示,我們將這兩個向量稱為基向量(也叫基底、基),如圖2-2所示。
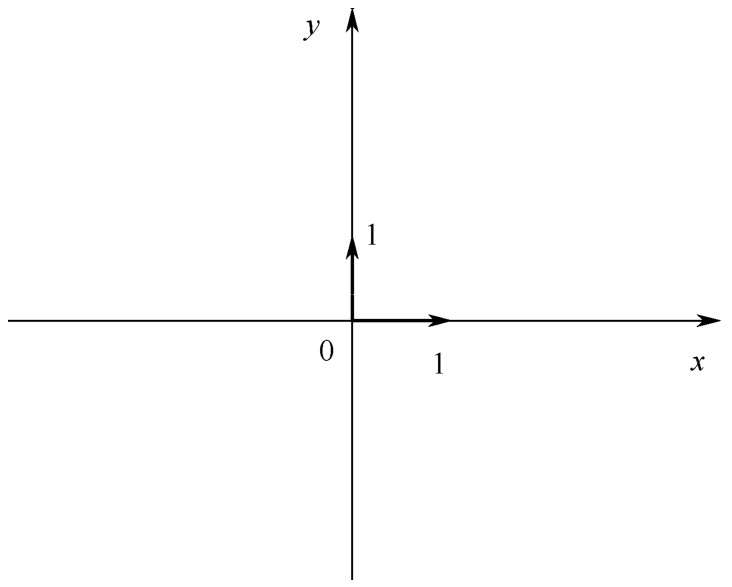
圖2-2 標準平面直角坐標系中的基向量
從圖2-2可以看到,基向量的長度都是1,這個坐標系是一個非常標準的直角坐標系。
對于坐標系內的任一坐標點(x, y),以坐標原點為起點向該坐標點做向量,記為a,易知 ,因此可以記作a=(x, y),這就是向量a的坐標表示,其坐標值可以看作基向量的倍乘。兩個基向量的坐標表示為(1, 0)和(0, 1)。
,因此可以記作a=(x, y),這就是向量a的坐標表示,其坐標值可以看作基向量的倍乘。兩個基向量的坐標表示為(1, 0)和(0, 1)。
例如,(1, 1)這個點可以理解為是由兩個基向量倍乘得到的,如下式所示。
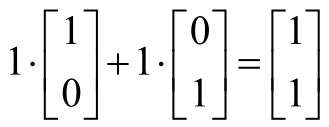
同樣,(2, 6)這個點可以理解為下式:
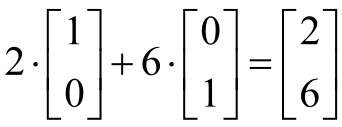
推薦閱讀