- 高等應用數學
- 閆柏玲
- 410字
- 2019-10-18 19:32:06
2.1.3 函數可導與連續的關系
函數連續與可導是函數的兩個重要性態,那么它們關系如何?先觀察函數y=|x|和 在原點的連續性與可導性,其圖像分別如圖2-2和圖2-3所示.
在原點的連續性與可導性,其圖像分別如圖2-2和圖2-3所示.
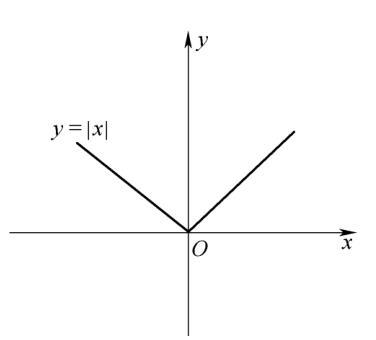
圖 2-2
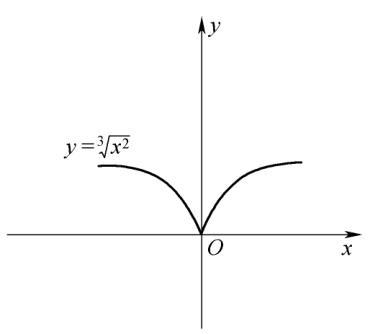
圖 2-3
直觀上觀察到兩個函數在定義域區間內的任何點處都是連續的.由于導數的幾何意義是曲線切線的斜率,顯然它們在坐標原點處不存在切線,所以它們在原點處不可導.因此,函數在某點處連續,在該點處不一定可導.那么,函數在該點處可導就一定連續嗎?下面用定理來回答.
定理2 如果函數y=f(x)在點x0處可導,則f(x)在點x0處一定連續.
證明 函數y=f(x)在點x0處可導,則 存在,因為
存在,因為
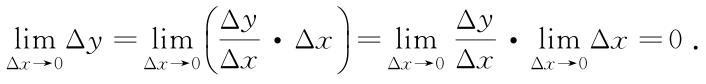
所以函數y=f(x)在點x0處連續.
下面舉例說明函數在點x0處連續,但在此點不可導.
例6 討論函數y=|x|在點x0=0處的連續性與可導性.
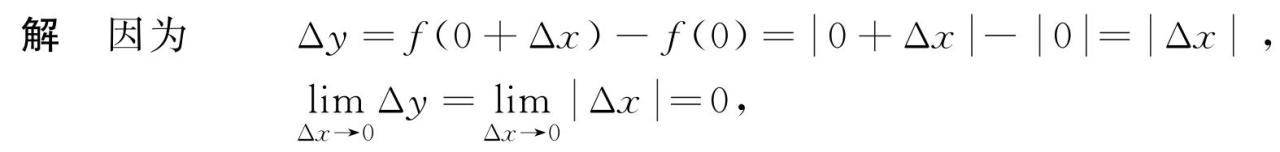
所以y=|x|點x0=0處連續.
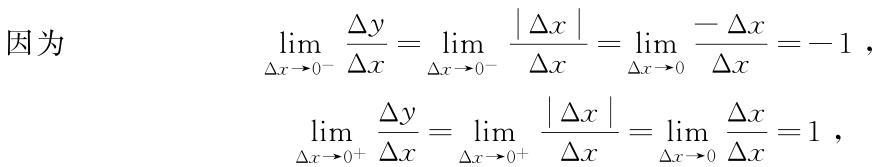
在x0=0處左、右導數不相等,所以  不存在,故在x0=0處函數y=|x|不可導.
不存在,故在x0=0處函數y=|x|不可導.
發現:若函數在某點可導,則其在該點一定連續;若函數在某點連續,則其在該點不一定可導;若函數在某點不連續,則其在該點一定不可導.