1.2 水電站線性調度函數

水庫群優化調度的目的是制定優化調度規則，以獲得較好的經濟效益，它主要有兩類基本途徑：顯隨機優化和隱隨機優化。顯隨機優化由于要求出徑流的條件概率轉移矩陣和計算上的“維數災”障礙，因此其應用受到限制；隱隨機優化方法一是針對給定的徑流序列，用確定性優化技術，為水庫群尋求最優運行方式；二是利用確定性優化得出的水庫群運行結果，制定水庫群調度函數。

1.2.1 線性調度函數與回歸分析

目前，短期徑流預報的精度已達到了實用的要求，將短期徑流預報結果用于水電站調度能取得較好的效益。考慮短期徑流預報普遍采用的優化調度函數為

ui=fi（Si,Ii），

式中：

Si——系統的時段初狀態（水位或存水量）；

Ii——面臨時段的徑流預報值；

ui——i時段的決策，一般取時段末狀態、時段出力或發電平均流量。

式中的fi一般來說是非線性的，處理起來很復雜。因為線性函數比較簡單，且任一光滑的非線性函數，在一定范圍內，都可用線性函數（切線或切面）來近似，所以，一般假設fi是線性的，即

ui=AiSi+BiIi+Ci，

式中，Ai,Bi,Ci——回歸系數。

由確定性長系列優化計算得到了水庫群系統中各水庫在確定來水條件下的長系列最優運行決策及對應的狀態過程線。計算結果揭示了水庫最優運行時其狀態、來水和決策之間的基本規律。從這些數據中辨識出各時段的優化調度函數的問題即是一個多變量線性回歸問題。

記Θ=（Ai,Bi,Ci）T為待辨識的參數，

為觀測數據矩陣，其中分別代表i時段第k年的水庫狀態、入庫流量和決策值。由線性回歸方法可知，回歸系數Θ滿足線性方程

對于回歸方程，我們總是希望從回歸方程中剔除那些可有可無的變量，以使建立的回歸方程更簡單。這就需要我們對每個自變量進行考察。顯然若某個自變量xj對y的作用不顯著，那么在回歸方程中，它的系數θi就可以取值為零。因此，檢驗變量xj對y是否顯著，等價于檢驗假設

H0:θj=0

對于假設檢驗，當然先要找統計量。由回歸分析我們知道

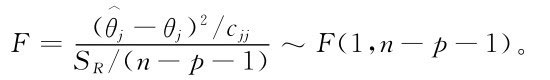
在假設（H0）下，可用

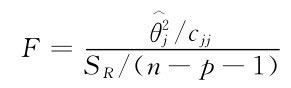
作為統計量來檢驗假設是否成立，即xj對y的影響是否顯著。其中，為xj的系數的估計值，SR為回歸殘差方差，cjj為矩陣（XTX）-1對角線上第j個元素。

對于給定顯著水平α，查F分布臨界值表得Fα，當統計量F＜Fα時，認為變量xj對y不顯著，可在回歸方程中去掉xj。選取最小的xj，重復檢驗過程，直到回歸方程中的每個變量都顯著為止。

上面的檢驗方法須計算矩陣（XTX）的逆，計算較復雜。可通過下面的分析步驟加以簡化，將xj從回歸方程中剔除掉（等價于令xj的系數為零），研究回歸殘差方差的變化，由此決定是否可以從回歸方程中剔除xj。此時有

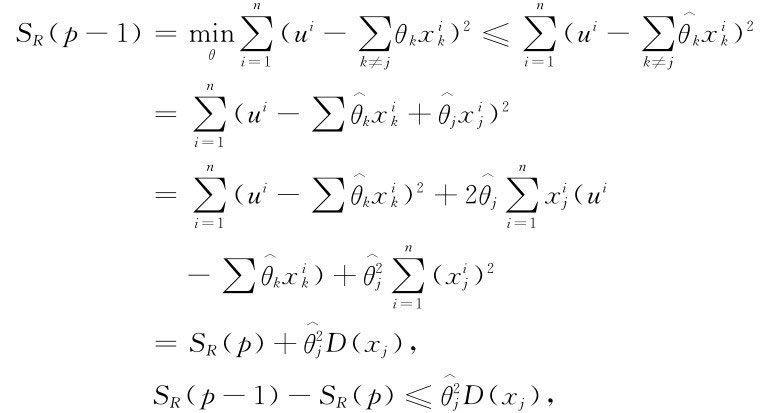
其中，D（xj）為變量xj的方差。

當·（n-p-1）＜Fα時，有

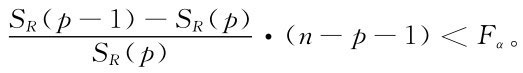
故可認為變量xj對y不顯著，可在回歸方程中去掉xj。重新建立回歸方程，選取最小的xj，重復檢驗過程，直到回歸方程中的每個變量都顯著為止。

以上通過F檢驗法來判斷某變量xj對y的顯著性，須人為選定顯著水平α，具有人為的主觀性。我們可用AIC準則來決定是否可從回歸方程中剔除掉xj。選取·D（xj）最小的xj，令xj的系數即去掉變量xj，建立回歸方程，計算殘差方差SR（p-1）和

AI C（p-1）=nlnSR（p-1）+2（p-1），

比較AIC（p）和AIC（p-1），若AIC（p）≥AIC（p-1），可認為變量xj對y不顯著，可在回歸方程中去掉xj。直到AIC（p）＜AIC（p-1）為止，得最佳回歸方程。

1.2.2 相鄰時段徑流獨立條件下的線性調度函數

由回歸分析我們知道，線性調度函數的形式為：——時段的平均入流值；——時段的平均決策值。

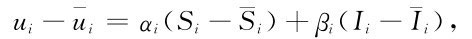
式中：

——時段的平均狀態；

則為狀態與平均值的偏差，是以前水庫入流的綜合反映和總結，與以后水庫來水無關，為來水與平均值的偏差，當徑流獨立時，也與以后水庫來水無關，這時與具有同等價值，如果以水庫存水量V為狀態，則調度函數中，其系數應相等，即），系數可由一元線性回歸方法得到

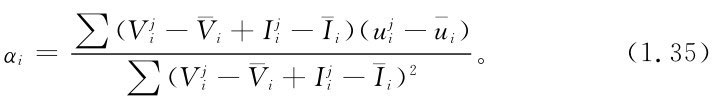
對水庫調度來說，決策變量可取發電流量Q，時段平均出力N，時段末水庫存水量V，末水位Z。由于這些變量之間是非線性的關系，如果用線性決策函數，選定決策變量后，其他一些變量就是非線性的，決策變量的選擇，對決策的結果有一定的影響。

在徑流獨立條件下，Vi--Vi+Ii--Ii反映時段總水量與平均情況水量的差，即是多出（少于）平時的部分，這部分的一部分通過泄流用來發電，一部分通過水庫儲存。

若選出庫流量為決策變量，且用線性決策函數，即設

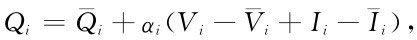
αi由式（1.35）計算，由水量平衡方程

Qi=Vi-Vi+1+Ii，

有，所以存水量為

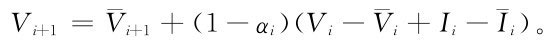
如果以庫存水量為決策變量，且用線性決策函數，可以證明用回歸分析計算出的決策函數將與此式相同。且殘差平方和與以出庫流量為決策變量的殘差平方和相等。事實上

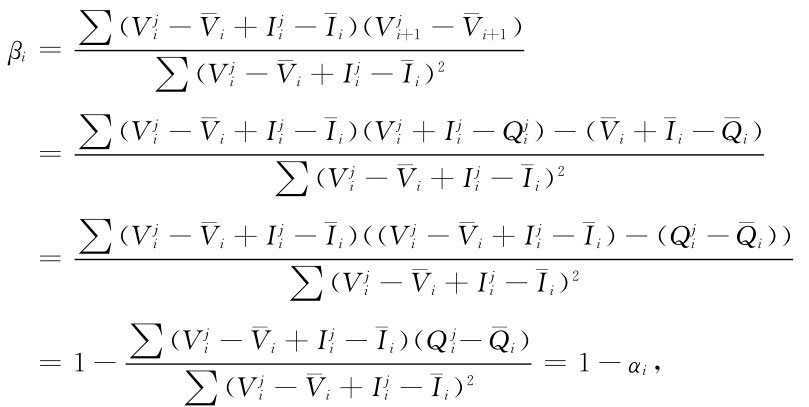
即以出庫流量為決策變量與以庫存水量為決策變量效果一樣。

當充分小時，決策流量用于發電可近似地用線性函數表示為

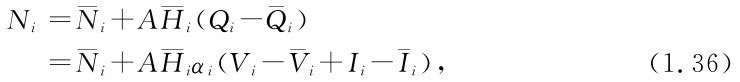
式中：

——平均水頭；

A——發電系數。

末水位可近似地用線性函數表示為

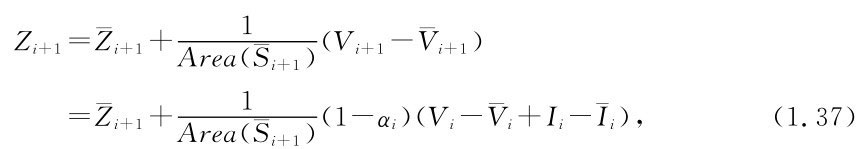
式中：

——末狀態平均值對應的水庫面積。

如果選出力為決策變量，并將出力值變換為

用式（1.35）計算系數，可得形如式（1.36）的調度規則，但此時的與以出庫流量為決策變量計算的αi一般是不會完全相等的。如果選末水位為決策變量，并將水位值變換為

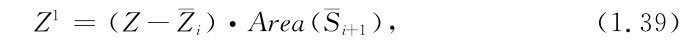
用式（1.35）計算系數，可得類似如式（1.37）的調度規則，但此時的系數與以庫存水量為決策變量計算的系數一般也是不會完全相等的。

我們注意到，水電站的最優調度線有這樣的一些規律，在不至于棄水的條件下（如枯水期），一般盡量抬高水位，這時一般只發保證出力，出力值比較有規律，水位變化可能比較大。而對有些時段，水位比較有規律，如防洪期末，水位一般為防洪限制水位。如果選擇決策變量，制定調度規則能反映這些規律，這樣的調度規則將會獲得較好的調度效果。

一個變量取值的規律性可由它的方差來衡量，方差小的規律性強。

1°.決策變量選擇原則1：最小方差原則統計計算變量Z1,N1,Qi或Vi+1的方差，以方差值最小的為決策變量。

進行式（1.37）、式（1.38）變換的目的是為了方差具有可比較性，但估計和可能會有誤差而影響方差的大小，當方差無顯著差異時，這一原則就不好確定決策變量。是一個隨機變量，Zi+1,Ni也可看成是隨機變量，它們與的相關系數反映它們對隨機變量的依賴程度，相關系數絕對值大的依賴性強，相關系數絕對值小的說明主要是自身的規律性，要找規律就應選相關系數小的。

2°.決策變量選擇原則2：相關系數絕對值最小原則統計計算變量Zi+1,Ni,Qi或Vi+1與的相關系數，以相關系數絕對值最小的為決策變量。

相關系數是一個無單位的量，常數因子不影響其絕對值，如X和Y的相關系數跟cX與Y的相關系數絕對值相等。事實上

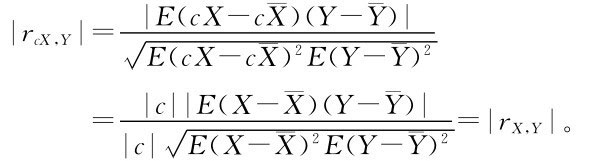
記，則，式（1.35）中回歸系數可寫成

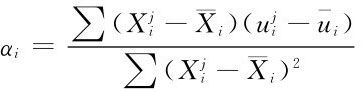
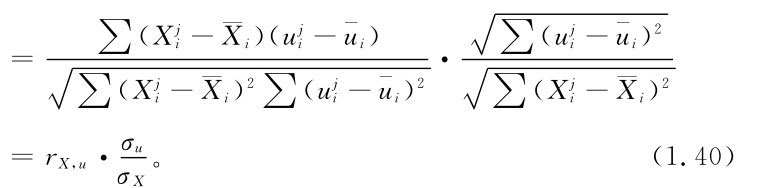
利用此式，上述兩個原則可綜合成如下原則：

3°.決策變量選擇原則3：回歸系數最小原則 由式（1.35）計算變量Z1,N1,Qi或Vi+1與的回歸系數，以回歸系數絕對值最小的為決策變量。

由于決策函數為,Xi為隨機變量，當用于實時決策時，Xi為預報值，預報總會有誤差，對較小的αi，由此作出的決策的誤差也較小，決策具有較好的穩定性。

1.2.3 線性決策函數的其他計算方法

由于是理想的最優決策，對于Xi的上述實現，如果能作出上述決策的實現值將是最好的，但假設線性決策后，一般是不可能的了。但我們可讓決策的方差實現原來的方差，對上述四種決策變量，從直觀上來看，其系數一般應是非負的，由此可得αi的簡化計算法

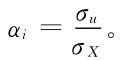
比較此式與式（1.40）可以看出，這種簡化計算相當于假設相關系數為1。

由式（1.36）、式（1.37），如果分別選變量Z1,N1為決策變量，由水量平衡方程，它們回歸系數的和應為1。如果再假設它們與X1的相關系數相等，由式（1.40），有

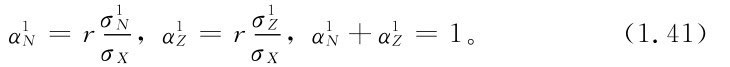
由此可得一簡化計算法

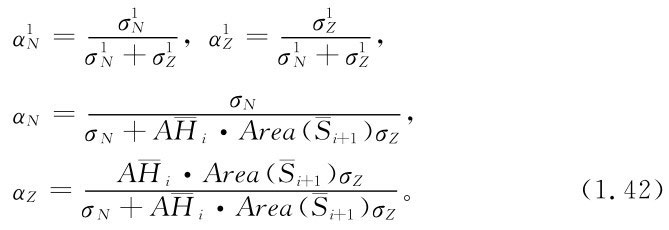
如果用式（1.40）計算出變量Z1的回歸系數，則取最小值，但考慮水量平衡條件，如果令，計算則并不一定也最小，反之也一樣。為此，要綜合考慮，在系數和為1的條件下，希望兩殘差平方和之和最小，即

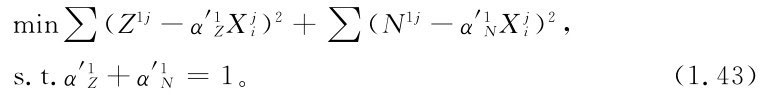
此式可化為

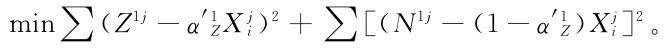
根據最優性必要條件，函數對的導數應為零，即

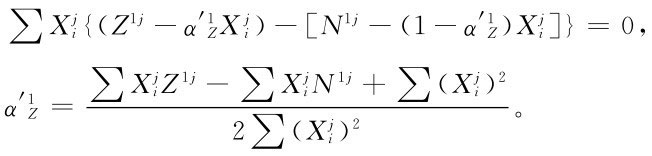
即

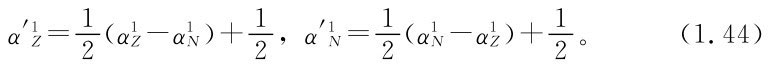
上式可化為

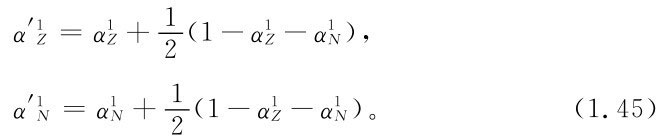
其中分別為用式（1.40）計算出的變量Z1,N1的回歸系數，為式（1.43）的最優解。由式（1.45）可以看出，用式（1.40）分別計算變量Z1,N1的回歸系數，如果所得結果正好滿足，則式（1.43）的最優解將與分別計算所得結果一致，如果不滿足條件，則式（1.43）的最優解將與分別計算所得結果不同，這時只需在原分別計算所得結果的基礎上稍作處理即可。

將式（1.44）變換為Z,N的回歸系數可得

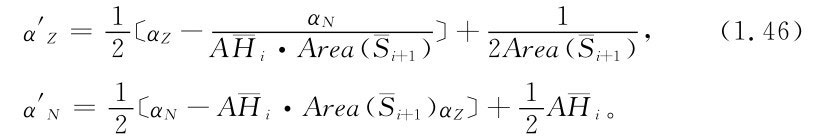
其中，αZ,αN分別為用式（1.40）計算出的變量Z,N的回歸系數。α′Z,α′N為考慮水量平衡條件，用變量Z,N聯合回歸所得的變量Z,N的回歸系數。

下面討論的計算方法：

在式（1.46）中，Z,N聯合回歸的回歸系數中，用到了平均水頭和平均狀態對應的水庫面積,和估計的精確度對由此計算的調度函數的好壞有直接的影響，下面考慮和平均狀態的計算方法。

由水頭計算公式：，可取

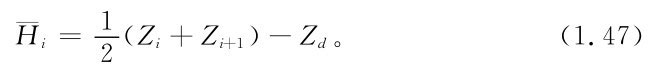
如果取水位為狀態，則

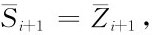
這時式（1.47）可寫成

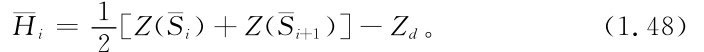
如果取庫容為狀態

這時，平均水頭為

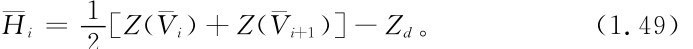
有必要討論上述兩種計算方法的異同，假設庫容曲線V（Z）具有二階連續導數，且二階導數大于零，由Taylor公式，存在使得

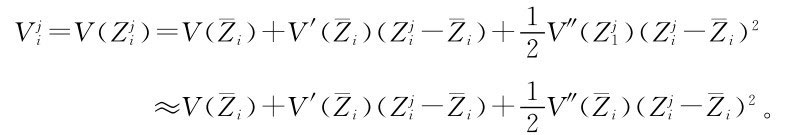
求和，除以n，可得

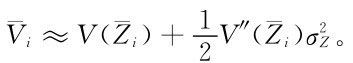
即對應的庫容比小，反過來，對應的水位比大，可折衷取

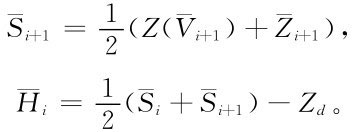
由于和都不是的無偏估計，用式（1.38）、式（1.39）變換所得系數也可能不是無偏的，由于最小二乘估計具有無偏性，為此可考慮用下述方法估計系數，求a,b使

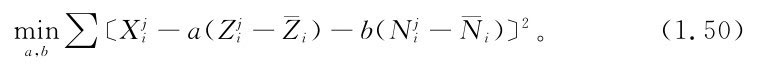
計算可得，由式（1.50）所得系數的估計值為

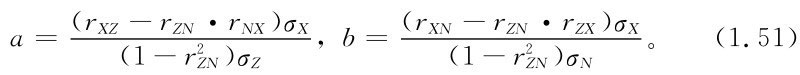
式中：

rxy——隨機變量x和y的統計相關系數；

σX——隨機變量X的標準差。

然后，由式（1.43）求回歸系數，即

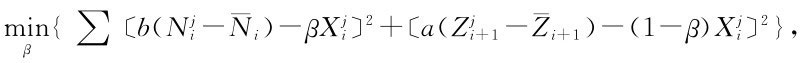
則

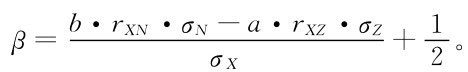
將式（1.51）代入此式得

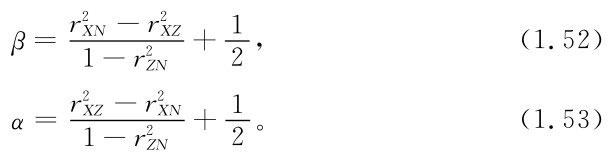
轉換為Z,N的回歸系數可得

1.2.4 線性調度函數的綜合計算方法

用不同的假設，求出m個線性調度函數uij=AijSi+BijIi+Cij（j=1,2,…,m），對同樣的狀態Si和徑流Ii，可作出m個決策uij，如果無法確定哪一個uij更好，則可取這m個決策的平均值為最終決策，這時決策相當于作一新的線性調度函數，其系數為原m個線性調度函數相應系數的平均值。

根據回歸分析，在一定假設條件下，回歸系數是一隨機變量，如果它是真值的無偏估計，則其期望值為真值，殘差可用來估計其方差。

若每個調度函數中的系數都是無偏估計，且是獨立的，則系數的平均值也是無偏估計，其方差為每個系數方差的1/m，也就是說，系數的平均值是比原來m個系數都好的估計值。

水庫調度中的決策變量有時段平均出力、時段平均泄流量、時段末水位和末庫容，用線性調度函數，選定決策變量后，其他變量就是狀態變量的非線性函數。

對某水電站，用如下7種方法分別求出線性調度函數的系數，然后，用系數的平均值作為最終調度函數的系數，這7種方法是：

（1）取時段平均出力為決策變量，由式（1.34）得

Ni=Ai1Vi+Bi1Ii+Ci1。

（2）取時段平均泄流量為決策變量，由式（1.34）計算系數αi 2,βi 2,γi 2，得Qi=αi2Vi+βi2Ii+γi2，然后，由

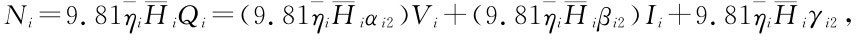
得

Ni=Ai2Vi+Bi2Ii+Ci2，

式中：

——平均效率；

——時段平均水頭。

（3）取時段平均出力為決策變量，由式（1.40）計算系數αi 3和γi 3得

Ni=αi3（Vi+Ii）+γi3=Ai3Vi+Bi3Ii+Ci3。

（4）取時段平均泄流量為決策變量，由式（1.40）計算系數αi 4和γi 4得

Qi=αi4（Vi+Ii）+γi4。

然后由得

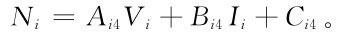
（5）由式（1.41）計算調度函數，取時段平均出力為決策變量，得

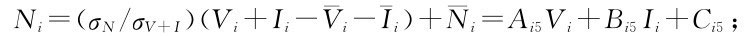
（6）由式（1.41）計算調度函數，取時段平均泄流量為決策變量，得

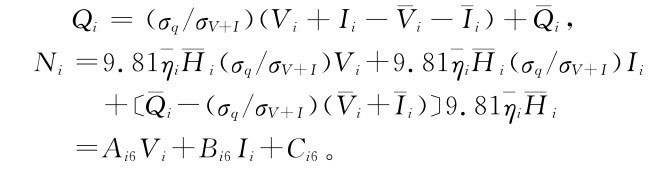
（7）由式（1.40），設時段平均泄流量和時段末庫存水量分別為

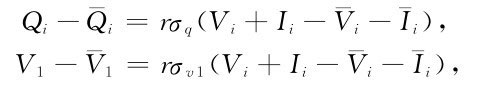
由水量平衡條件V1+Qi=Vi+Ii，得

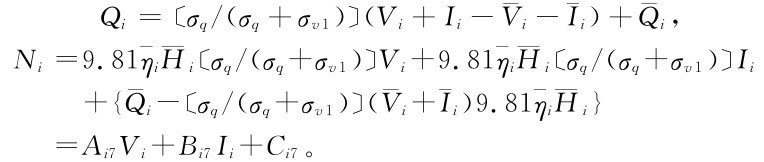
最后，求線性調度函數

Ni=AiVi+BiIi+Ci

其中

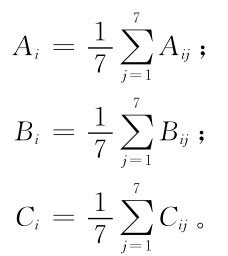
計算部分結果如表1.1所示。

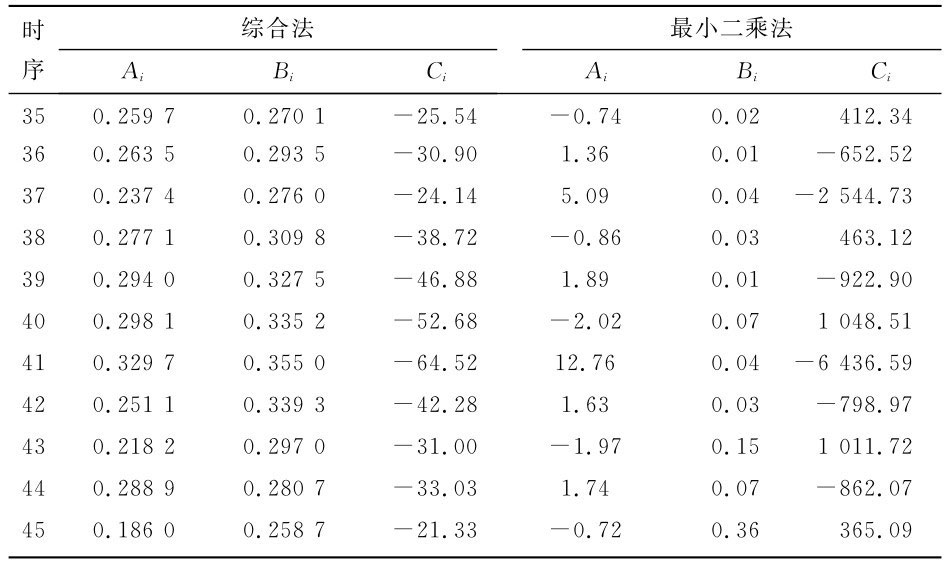
由表1.1的計算結果可以看出，最終的調度函數中系數Ai和Bi沒有負數，且系數具有連續性，比直接用二元線性回歸方法更符合實際。