2014年全國(guó)計(jì)算機(jī)等級(jí)考試3年真題精解與過(guò)關(guān)全真訓(xùn)練題:二級(jí)Access數(shù)據(jù)庫(kù)程序設(shè)計(jì)
- 2014年全國(guó)計(jì)算機(jī)等級(jí)考試3年真題精解與過(guò)關(guān)全真訓(xùn)練題:二級(jí)Access數(shù)據(jù)庫(kù)程序設(shè)計(jì)
- 希賽教育等考學(xué)院 彭雪陽(yáng)主編
- 13203字
- 2019-01-01 00:31:18
1.1 考點(diǎn)精講
根據(jù)考試大綱,本章主要考查以下知識(shí)點(diǎn):
1)算法的基本概念;算法復(fù)雜度的概念和意義(時(shí)間復(fù)雜度與空間復(fù)雜度)。
2)數(shù)據(jù)結(jié)構(gòu)的定義;數(shù)據(jù)的邏輯結(jié)構(gòu)與存儲(chǔ)結(jié)構(gòu),數(shù)據(jù)結(jié)構(gòu)的圖形表示,線性結(jié)構(gòu)與非線性結(jié)構(gòu)的概念。
3)線性表的定義;線性表的順序存儲(chǔ)結(jié)構(gòu)及其插入與刪除運(yùn)算。
4)棧和隊(duì)列的定義;棧和隊(duì)列的順序存儲(chǔ)結(jié)構(gòu)及其基本運(yùn)算。
5)線性單鏈表、雙向鏈表與循環(huán)鏈表的結(jié)構(gòu)及其基本運(yùn)算。
6)樹的基本概念;二叉樹的定義及其存儲(chǔ)結(jié)構(gòu);二叉樹的前序、中序和后序遍歷。
7)順序查找與二分法查找算法;基本排序算法(交換類排序、選擇類排序、插入類排序)。
1.1.1 算法與數(shù)據(jù)結(jié)構(gòu)概述
本節(jié)的主要考點(diǎn)集中在算法與數(shù)據(jù)結(jié)構(gòu)的基本概念上,包括算法的基本特征、復(fù)雜度,以及數(shù)據(jù)結(jié)構(gòu)的表示等。
1.算法的概念
算法(Algorithm)是一系列解決問(wèn)題的清晰指令,也就是說(shuō),能夠?qū)σ欢ㄒ?guī)范的輸入,在有限時(shí)間內(nèi)得到所要求的輸出的步驟。如果一個(gè)算法有缺陷,或不適合某個(gè)問(wèn)題,執(zhí)行這個(gè)算法將不會(huì)解決這個(gè)問(wèn)題。不同的算法完成同樣的任務(wù)可能有不同的時(shí)間、空間或效率。
(1)算法的基本特征
1)有窮性(Finiteness):算法必須能在執(zhí)行有限個(gè)步驟之后終止。
2)確定性(Definiteness):算法的每一步驟必須有確切的定義。
3)輸入項(xiàng)(Input):一個(gè)算法有0個(gè)或多個(gè)輸入,以刻畫運(yùn)算對(duì)象的初始情況,所謂0個(gè)輸入是指算法本身定出了初始條件。
4)輸出項(xiàng)(Output):一個(gè)算法有一個(gè)或多個(gè)輸出,以反映對(duì)輸入數(shù)據(jù)加工后的結(jié)果。沒有輸出的算法是毫無(wú)意義的。
5)可行性(Effectiveness):也稱有效性,算法中執(zhí)行的任何計(jì)算步都可以被分解為基本的、可執(zhí)行的操作步,即每個(gè)計(jì)算步都可以在有限時(shí)間內(nèi)完成。
(2)算法的基本要素
算法中對(duì)數(shù)據(jù)的運(yùn)算和操作:每個(gè)算法實(shí)際上是按解題要求從環(huán)境能進(jìn)行的所有操作中選擇合適的操作所組成的一組指令序列。
計(jì)算機(jī)可以執(zhí)行的基本操作是以指令的形式描述的。一個(gè)計(jì)算機(jī)系統(tǒng)能執(zhí)行的所有指令的集合,稱為該計(jì)算機(jī)系統(tǒng)的指令系統(tǒng)。計(jì)算機(jī)程序就是按解題要求從計(jì)算機(jī)指令系統(tǒng)中選擇合適的指令所組成的指令序列。在一般的計(jì)算機(jī)系統(tǒng)中,基本的運(yùn)算和操作有以下4類。
1)算術(shù)運(yùn)算:主要包括加、減、乘、除等運(yùn)算。
2)邏輯運(yùn)算:主要包括與、或、非等運(yùn)算。
3)關(guān)系運(yùn)算:主要包括大于、小于、等于、不等于等運(yùn)算。
4)數(shù)據(jù)傳輸:主要包括賦值、輸入、輸出等操作。
算法的控制結(jié)構(gòu):一個(gè)算法的功能不僅僅取決于所選用的操作,而且還與各操作之間的執(zhí)行順序有關(guān)。算法中各操作之間的執(zhí)行順序稱為算法的控制結(jié)構(gòu)。
(3)算法設(shè)計(jì)的基本方法
計(jì)算機(jī)算法不同于人工處理的方法,下面是工程上常用的幾種算法設(shè)計(jì)。在實(shí)際應(yīng)用時(shí),各種方法之間往往存在著一定的聯(lián)系。
1)遞推法:遞推法是利用問(wèn)題本身所具有的一種遞推關(guān)系求解問(wèn)題的一種方法。它把問(wèn)題分成若干步,找出相鄰幾步的關(guān)系,從而達(dá)到目的。
2)遞歸法:遞歸法指的是一個(gè)過(guò)程。函數(shù)不斷引用自身,直到引用的對(duì)象已知。
3)窮舉搜索法:窮舉搜索法是對(duì)可能是解的眾多候選解按某種順序進(jìn)行逐一枚舉和檢驗(yàn),并從中找出那些符合要求的候選解作為問(wèn)題的解。
4)貪婪法:貪婪法是一種不追求最優(yōu)解,只希望得到較為滿意解的方法。貪婪法一般可以快速得到滿意的解,因?yàn)樗∪チ藶檎易顑?yōu)解要窮盡所有可能而必須耗費(fèi)的大量時(shí)間。貪婪法常以當(dāng)前情況為基礎(chǔ)做最優(yōu)選擇,而不考慮各種可能的整體情況,所以貪婪法不要回溯。
5)分治法:分治法是把一個(gè)復(fù)雜的問(wèn)題分成兩個(gè)或更多相同或相似的子問(wèn)題,再把子問(wèn)題分成更小的子問(wèn)題,直到最后子問(wèn)題可以簡(jiǎn)單地直接求解,原問(wèn)題的解即子問(wèn)題的解的合并。
6)動(dòng)態(tài)規(guī)劃法:動(dòng)態(tài)規(guī)劃法是一種在數(shù)學(xué)和計(jì)算機(jī)科學(xué)中使用的,用于求解包含重疊子問(wèn)題的最優(yōu)化問(wèn)題的方法。其基本思想是,將原問(wèn)題分解為相似的子問(wèn)題,在求解的過(guò)程中通過(guò)子問(wèn)題的解求出原問(wèn)題的解。動(dòng)態(tài)規(guī)劃的思想是多種算法的基礎(chǔ),被廣泛應(yīng)用于計(jì)算機(jī)科學(xué)和工程領(lǐng)域。
7)迭代法:迭代法是數(shù)值分析中通過(guò)從一個(gè)初始估計(jì)解出發(fā)尋找一系列近似解來(lái)解決問(wèn)題(一般是解方程或者方程組)的過(guò)程,為實(shí)現(xiàn)這一過(guò)程所使用的方法統(tǒng)稱為迭代法。
(4)良好的算法設(shè)計(jì)的要求
一個(gè)良好的算法應(yīng)達(dá)到如下目標(biāo)。
1)正確性(Correctness):算法的計(jì)算結(jié)果必須是正確的。
2)可讀性(Readability):可讀性好有助于用戶對(duì)算法的理解;不易理解的程序容易隱藏較多錯(cuò)誤,難以調(diào)試和修改。
3)健壯性(Robustness):當(dāng)輸入數(shù)據(jù)非法時(shí),算法也能適當(dāng)?shù)刈龀龇磻?yīng)或進(jìn)行處理,而不會(huì)產(chǎn)生莫名其妙的輸出結(jié)果。
4)效率與低存儲(chǔ)量需求:效率指的是程序執(zhí)行時(shí),對(duì)于同一個(gè)問(wèn)題如果有多個(gè)算法可以解決,執(zhí)行時(shí)間短的算法效率高;存儲(chǔ)量需求指算法執(zhí)行過(guò)程中所需要的最大存儲(chǔ)空間。
2.算法的復(fù)雜度
算法復(fù)雜度分為空間復(fù)雜度和時(shí)間復(fù)雜度。
(1)算法的時(shí)間復(fù)雜度
算法的時(shí)間復(fù)雜度是指執(zhí)行算法所需要的計(jì)算工作量。同一個(gè)算法用不同的語(yǔ)言實(shí)現(xiàn),或者用不同的編譯程序進(jìn)行編譯,或者在不同的計(jì)算機(jī)上運(yùn)行,效率均不同。
(2)算法的空間復(fù)雜度
算法的空間復(fù)雜度是指執(zhí)行這個(gè)算法所需要的內(nèi)存空間。一個(gè)算法所占用的存儲(chǔ)空間包括算法程序所占的存儲(chǔ)空間、輸入的初始數(shù)據(jù)所占的存儲(chǔ)空間,以及算法執(zhí)行中所需要的額外空間。
3.數(shù)據(jù)結(jié)構(gòu)的定義
數(shù)據(jù)結(jié)構(gòu)(Data Structure)是指相互之間存在一種或多種特定關(guān)系的數(shù)據(jù)元素的集合。
數(shù)據(jù)(Data)是對(duì)客觀事物的符號(hào)表示,在計(jì)算機(jī)科學(xué)中是指所有能輸入到計(jì)算機(jī)中并被計(jì)算機(jī)程序處理的符號(hào)的總稱。
數(shù)據(jù)元素(Data Element)是數(shù)據(jù)的基本單位,在計(jì)算機(jī)程序中通常作為一個(gè)整體進(jìn)行考慮和處理。
在一般情況下,在具有相同特征的數(shù)據(jù)元素集合中,各個(gè)數(shù)據(jù)元素之間存在某種關(guān)系(即連續(xù)),這種關(guān)系反映了該集合中的數(shù)據(jù)元素所固有的一種結(jié)構(gòu)。在數(shù)據(jù)處理領(lǐng)域中,通常把數(shù)據(jù)元素之間這種固有的關(guān)系簡(jiǎn)單地用前后件關(guān)系(或直接前驅(qū)與直接后繼關(guān)系)來(lái)描述。
一般來(lái)說(shuō),數(shù)據(jù)元素之間的任何關(guān)系都可以用前后件關(guān)系來(lái)描述。
(1)數(shù)據(jù)的邏輯結(jié)構(gòu)
數(shù)據(jù)結(jié)構(gòu)是指反映數(shù)據(jù)元素之間的關(guān)系的數(shù)據(jù)元素集合的表示。通俗地說(shuō),數(shù)據(jù)結(jié)構(gòu)是指帶有結(jié)構(gòu)的數(shù)據(jù)元素的集合。所謂結(jié)構(gòu)實(shí)際上就是指數(shù)據(jù)元素之間的前后件關(guān)系。
一個(gè)數(shù)據(jù)結(jié)構(gòu)應(yīng)包含兩方面信息:表示數(shù)據(jù)元素的信息和表示各數(shù)據(jù)元素之間的前后件關(guān)系的信息。
數(shù)據(jù)的邏輯結(jié)果是對(duì)數(shù)據(jù)元素之間的邏輯關(guān)系的描述。它可以用一個(gè)數(shù)據(jù)元素的集合和在此集合中定義的若干關(guān)系來(lái)表示。用D表示數(shù)據(jù)元素的集合,用R表示數(shù)據(jù)元素之間的前后件關(guān)系,即一個(gè)數(shù)據(jù)結(jié)構(gòu)可以表示為B=(D,R),這是一個(gè)二元關(guān)系的表示方式。
(2)數(shù)據(jù)的存儲(chǔ)結(jié)構(gòu)
數(shù)據(jù)的邏輯結(jié)構(gòu)在計(jì)算機(jī)存儲(chǔ)空間中的存放形式,稱為數(shù)據(jù)的存儲(chǔ)結(jié)構(gòu)(也稱為數(shù)據(jù)的物理結(jié)構(gòu))。
由于數(shù)據(jù)元素在計(jì)算機(jī)存儲(chǔ)空間中的位置關(guān)系可能與邏輯關(guān)系不同,因此,為了表示存放在計(jì)算機(jī)存儲(chǔ)空間中的各數(shù)據(jù)元素之間的邏輯關(guān)系(即前后件關(guān)系),在數(shù)據(jù)的存儲(chǔ)結(jié)構(gòu)中,不僅要存放各數(shù)據(jù)元素的信息,還需要存放各數(shù)據(jù)元素之間的前后件關(guān)系的信息。
一種數(shù)據(jù)的邏輯結(jié)構(gòu)根據(jù)需要可以表示成多種存儲(chǔ)結(jié)構(gòu),常用的存儲(chǔ)結(jié)構(gòu)有順序、鏈接、索引等,而采用不同的存儲(chǔ)結(jié)構(gòu),其數(shù)據(jù)處理的效率是不同的。因此,在進(jìn)行數(shù)據(jù)處理時(shí),選擇合適的存儲(chǔ)結(jié)構(gòu)是很重要的。
4.數(shù)據(jù)結(jié)構(gòu)的表示
數(shù)據(jù)結(jié)構(gòu)的表示除了用二元關(guān)系表示外,還可以直觀地用圖形表示。
在數(shù)據(jù)結(jié)構(gòu)的圖形表示中,對(duì)于數(shù)據(jù)集合D中的每一個(gè)數(shù)據(jù)元素用中間標(biāo)有元素值的方框表示,一般稱之為數(shù)據(jù)節(jié)點(diǎn),簡(jiǎn)稱為節(jié)點(diǎn)。為了進(jìn)一步表示各數(shù)據(jù)元素之間的前后件關(guān)系,對(duì)于關(guān)系R中的每一個(gè)二元組,用一條有向線段從前件節(jié)點(diǎn)指向后件節(jié)點(diǎn)。
在數(shù)據(jù)結(jié)構(gòu)中,沒有前件的節(jié)點(diǎn)稱為根節(jié)點(diǎn);沒有后件的節(jié)點(diǎn)稱為終端節(jié)點(diǎn)(也稱為葉子節(jié)點(diǎn))。
一個(gè)數(shù)據(jù)結(jié)構(gòu)中的節(jié)點(diǎn)可能是在動(dòng)態(tài)變化的。根據(jù)需要或在處理過(guò)程中,可以在一個(gè)數(shù)據(jù)結(jié)構(gòu)中增加一個(gè)新節(jié)點(diǎn)(稱為插入運(yùn)算),也可以刪除數(shù)據(jù)結(jié)構(gòu)中的某個(gè)節(jié)點(diǎn)(稱為刪除運(yùn)算)。插入與刪除是對(duì)數(shù)據(jù)結(jié)構(gòu)的兩種基本運(yùn)算。除此之外,對(duì)數(shù)據(jù)結(jié)構(gòu)的運(yùn)算還有查找、分類、合并、分解、復(fù)制和修改等。
5.線性結(jié)構(gòu)與非線性結(jié)構(gòu)
根據(jù)數(shù)據(jù)結(jié)構(gòu)中各數(shù)據(jù)元素之間前后件關(guān)系的復(fù)雜程度,一般將數(shù)據(jù)結(jié)構(gòu)分為兩大類型:線性結(jié)構(gòu)與非線性結(jié)構(gòu)。
線性結(jié)構(gòu)滿足以下條件:
1)有且只有一個(gè)根節(jié)點(diǎn)。
2)每一個(gè)節(jié)點(diǎn)最多有一個(gè)前件,也最多只有一個(gè)后件。
如果一個(gè)數(shù)據(jù)結(jié)構(gòu)不是線性結(jié)構(gòu),則稱之為非線性結(jié)構(gòu)。如果在一個(gè)數(shù)據(jù)結(jié)構(gòu)中一個(gè)數(shù)據(jù)元素都沒有,則稱該數(shù)據(jù)結(jié)構(gòu)為空。線性結(jié)構(gòu)與非線性結(jié)構(gòu)都可以是空的數(shù)據(jù)結(jié)構(gòu)。對(duì)于空的數(shù)據(jù)結(jié)構(gòu),如果對(duì)該數(shù)據(jù)結(jié)構(gòu)的運(yùn)算是按線性結(jié)構(gòu)的規(guī)則來(lái)處理的,則屬于線性結(jié)構(gòu),否則屬于非線性結(jié)構(gòu)。
1.1.2 線性表
本節(jié)主要考查線性表的基本概念,以及線性表的順序存儲(chǔ)方式。
1.線性表概述
線性表是一種常用的數(shù)據(jù)結(jié)構(gòu)。
在實(shí)際應(yīng)用中,線性表都是以棧、隊(duì)列、字符串、數(shù)組等特殊線性表的形式來(lái)使用的。由于這些特殊線性表都具有各自的特性,因此,掌握這些特殊線性表的特性,對(duì)于數(shù)據(jù)運(yùn)算的可靠性和提高操作效率都是至關(guān)重要的。
線性表是一個(gè)線性結(jié)構(gòu),它是一個(gè)含有n(n≥0)個(gè)節(jié)點(diǎn)的有限序列,對(duì)于其中的節(jié)點(diǎn),有且僅有一個(gè)開始節(jié)點(diǎn)沒有前驅(qū)(前件)節(jié)點(diǎn)但有一個(gè)后繼(后件)節(jié)點(diǎn),有且僅有一個(gè)終端節(jié)點(diǎn)沒有后繼節(jié)點(diǎn)但有一個(gè)前驅(qū)節(jié)點(diǎn),其他的節(jié)點(diǎn)都有且僅有一個(gè)前驅(qū)節(jié)點(diǎn)和一個(gè)后繼節(jié)點(diǎn)。一般來(lái)說(shuō),一個(gè)線性表可以表示成一個(gè)線性序列:k1,k2,…,kn,其中k1是開始節(jié)點(diǎn),kn是終端節(jié)點(diǎn)。
線性結(jié)構(gòu)的基本特征如下:
1)集合中必存在唯一的一個(gè)“第一元素”。
2)集合中必存在唯一的一個(gè)“最后元素”。
3)除最后一個(gè)元素之外,每個(gè)元素均有唯一的后繼。
4)除第一個(gè)元素之外,每個(gè)元素均有唯一的前驅(qū)。
由n(n≥0)個(gè)數(shù)據(jù)元素(節(jié)點(diǎn))a1,a2,…,an組成的有限序列,數(shù)據(jù)元素的個(gè)數(shù)n定義為表的長(zhǎng)度。當(dāng)n=0時(shí)稱為空表。常常將非空的線性表(n﹥0)記作:(a1,a2,…,an)。
2.線性表的順序存儲(chǔ)
線性表的順序存儲(chǔ)指的是用一組地址連續(xù)的存儲(chǔ)單元依次存儲(chǔ)線性表的數(shù)據(jù)元素。線性表的順序存儲(chǔ)又叫作順序表。
(1)線性表的順序存儲(chǔ)基本概念
線性表的順序存儲(chǔ)結(jié)構(gòu)具備以下兩個(gè)基本特征:
1)線性表中的所有元素所占的存儲(chǔ)空間是連續(xù)的。
2)線性表中各數(shù)據(jù)元素在存儲(chǔ)空間中是按邏輯順序依次存放的。
假設(shè)線性表的每個(gè)元素需要占用k個(gè)存儲(chǔ)單元,并且所占的存儲(chǔ)位置ADR(ai+1)和第i個(gè)數(shù)據(jù)元素的存儲(chǔ)位置ADR(ai)之間滿足下列關(guān)系:
ADR(ai+1)=ADR(ai)+k
線性表第i個(gè)元素ai的存儲(chǔ)位置為:
ADR(ai)=ADR(a1)+(i-1)×k
公式中ADR(a1)是線性表的第一個(gè)數(shù)據(jù)元素的存儲(chǔ)位置,通常稱為線性表的起始位置或基址。
在C語(yǔ)言中,通常定義一個(gè)一維數(shù)組來(lái)表示線性表的順序存儲(chǔ)空間,如圖1-1所示。
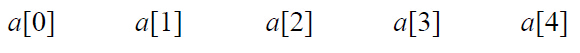
圖1-1 順序存儲(chǔ)
在用一維數(shù)組存放線性表時(shí),該一維數(shù)組的長(zhǎng)度通常要定義得比線性表的實(shí)際長(zhǎng)度大一些,以便對(duì)線性表進(jìn)行各種運(yùn)算,特別是插入運(yùn)算。
在線性表的順序存儲(chǔ)結(jié)構(gòu)下,可以對(duì)線性表做以下運(yùn)算:
1)在線性表的指定位置處加入一個(gè)新的元素(即線性表的插入)。
2)在線性表中刪除指定的元素(即線性表的刪除)。
3)在線性表中查找某個(gè)(或某些)特定的元素(即線性表的查找)。
4)對(duì)線性表中的元素進(jìn)行排序(即線性表的排序)。
5)將一個(gè)線性表分解成多個(gè)線性表(即線性表的分解)。
6)將多個(gè)線性表合并成一個(gè)線性表(即線性表的合并)。
7)復(fù)制一個(gè)線性表(即線性表的復(fù)制)。
8)逆轉(zhuǎn)一個(gè)線性表(即線性表的逆轉(zhuǎn))。
(2)順序表的基本操作
順序表的基本操作包括插入運(yùn)算和刪除運(yùn)算。
1)順序表的插入運(yùn)算:線性表的插入運(yùn)算是指在表的第i(1≤i≤n+l)個(gè)位置上,插入一個(gè)新節(jié)點(diǎn)x,使長(zhǎng)度為n的線性表(a1,…,ai-1,ai,…,an)變成長(zhǎng)度為n+1的線性表(a1,…,ai-1,x,ai,…,an+1)。
現(xiàn)在分析算法的復(fù)雜度。設(shè)它的值為n。該算法的時(shí)間主要花費(fèi)在循環(huán)節(jié)點(diǎn)后移語(yǔ)句上,該語(yǔ)句的執(zhí)行次數(shù)(即移動(dòng)節(jié)點(diǎn)的次數(shù))是n-1+1。由此可看出,所需移動(dòng)節(jié)點(diǎn)的次數(shù)不僅依賴于表的長(zhǎng)度,而且還與插入位置有關(guān)。
當(dāng)i=n+1時(shí),由于循環(huán)變量的終值大于初值,節(jié)點(diǎn)后移語(yǔ)句將不執(zhí)行。這是最好的情況,其時(shí)間復(fù)雜度為O(1)。
當(dāng)i=1時(shí),節(jié)點(diǎn)后移語(yǔ)句將循環(huán)執(zhí)行n次,需移動(dòng)表中所有節(jié)點(diǎn)。這是最壞的情況,其時(shí)間復(fù)雜度為O(n)。
綜合以上的情況,得出算法的平均時(shí)間復(fù)雜度為O(n)。
2)順序表的刪除運(yùn)算:線性表的刪除運(yùn)算是指將表的第i(1≤i≤n)個(gè)節(jié)點(diǎn)刪除,使長(zhǎng)度為n的線性表(a1,…,ai-1,ai,ai+1,…,an)變成長(zhǎng)度為n-l的線性表(a1,…,ai-1,ai+1,…,an-1)。
該算法的時(shí)間分析與插入算法相似,節(jié)點(diǎn)的移動(dòng)次數(shù)也是由表長(zhǎng)n和位置i決定的。
若i=n,則由于循環(huán)變量的初值大于終值,前移語(yǔ)句將不執(zhí)行,無(wú)需移動(dòng)節(jié)點(diǎn)。
若i=1,則前移語(yǔ)句將循環(huán)執(zhí)行n-1次,需移動(dòng)表中除開始節(jié)點(diǎn)外的所有節(jié)點(diǎn)。這兩種情況下算法的時(shí)間復(fù)雜度分別為O(1)和O(n)。
綜合以上的情況得出,在順序表上做刪除運(yùn)算,平均要移動(dòng)表中約一半的節(jié)點(diǎn),平均時(shí)間復(fù)雜度也是O(n)。
1.1.3 棧和隊(duì)列
棧和隊(duì)列都是特殊的線性表,其定義符合線性表的定義,其操作也類似于線性表的操作,只不過(guò)增加了一些限定而已。
1.棧的定義與操作
棧(Stack)是一種特殊的線性表。棧是只能在表的一端進(jìn)行插入和刪除運(yùn)算的線性表。通常稱插入、刪除的這一端為棧頂(Top),另一端為棧底(Bottom),如圖1-2所示。當(dāng)表中沒有元素時(shí)稱為空棧。棧頂元素總是后插入的元素,也是最先被刪除的元素;棧底元素總是最先被插入的元素,也是最后才能被刪除的元素。
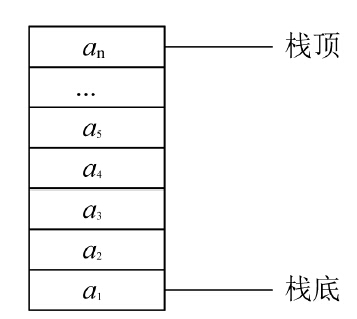
圖1-2 棧
假設(shè)棧S=(al,a2,a3,…,an),則a1為棧底元素,an為棧頂元素。棧中元素按a1,a2,a3,…,an的次序進(jìn)棧,退棧的第一個(gè)元素應(yīng)為棧頂元素,換句話說(shuō),棧的修改是按后進(jìn)先出的原則進(jìn)行的。因此,棧稱為先進(jìn)后出表(First In Last Out,F(xiàn)ILO),或后進(jìn)先出表(Last In First Out,LIFO)。
棧的操作主要有入棧運(yùn)算、退棧運(yùn)算(出棧)和讀棧頂元素。
1)入棧運(yùn)算:入棧運(yùn)算是指在棧頂位置插入一個(gè)新元素。首先將棧頂指針加1(即Top加1),然后將元素插入到棧頂指針指向的位置。當(dāng)棧頂指針已經(jīng)指向存儲(chǔ)空間的最后一個(gè)位置時(shí),說(shuō)明棧空間已滿,不能再進(jìn)行入棧操作,這種情況稱為棧“上溢”錯(cuò)誤。
2)退棧運(yùn)算:退棧是指取出棧頂元素并賦給一個(gè)指定的變量。首先將棧頂元素(棧頂指針指向的元素)賦給一個(gè)指定的變量,然后將棧頂指針減1(即Top減1)。當(dāng)棧頂指針為0時(shí),說(shuō)明棧空,不可進(jìn)行退棧操作,這種情況稱為棧的“下溢”錯(cuò)誤。
3)讀棧頂元素:讀棧頂元素是指將棧頂元素賦給一個(gè)指定的變量。這個(gè)運(yùn)算不刪除棧頂元素,只是將它賦給一個(gè)變量,因此棧頂指針不會(huì)改變。當(dāng)棧頂指針為0時(shí),說(shuō)明棧空,讀不到棧頂元素。
2.隊(duì)列的定義與操作
隊(duì)列(Queue)是只允許在一端刪除、在另一端插入的順序表。允許刪除的一端叫作隊(duì)頭(Front),允許插入的一端叫作隊(duì)尾(Rear),如圖1-3所示。
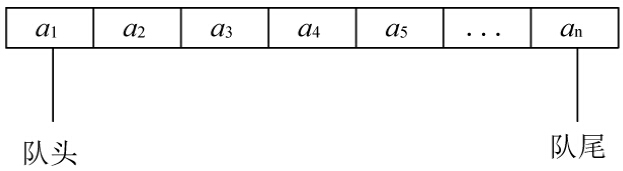
圖1-3 隊(duì)列
(1)隊(duì)列的運(yùn)算
當(dāng)隊(duì)列中沒有元素時(shí)稱為空隊(duì)列。在空隊(duì)列中依次加入元素a1,a2,…,an之后,a1是隊(duì)頭元素,an是隊(duì)尾元素。顯然退出隊(duì)列的次序也只能是a1,a2,…,an,也就是說(shuō)隊(duì)列的修改是按先進(jìn)先出的原則進(jìn)行的。因此隊(duì)列亦稱為先進(jìn)先出的線性表,或后進(jìn)后出的線性表。
1)入隊(duì)操作:往隊(duì)列隊(duì)尾插入一個(gè)元素稱為入隊(duì)運(yùn)算。
2)出隊(duì)操作:從隊(duì)列隊(duì)頭刪除一個(gè)元素稱為出隊(duì)運(yùn)算。
(2)循環(huán)隊(duì)列的運(yùn)算
所謂循環(huán)隊(duì)列,就是將隊(duì)列存儲(chǔ)空間的最后一個(gè)位置繞到第一個(gè)位置,形成邏輯上的環(huán)狀空間。
在循環(huán)隊(duì)列中,用隊(duì)尾指針Rear指向隊(duì)列中的隊(duì)尾元素,用隊(duì)頭指針Front指向排頭元素的前一個(gè)位置。因此,從排頭指針Front指向的后一個(gè)位置直到隊(duì)尾指針Rear指向的位置之間的所有元素均為隊(duì)列中的元素。
在循環(huán)隊(duì)列中進(jìn)行出隊(duì)、入隊(duì)操作時(shí),頭尾指針仍要加1,朝前移動(dòng)。只不過(guò)當(dāng)頭尾指針指向向量上界(Queuesize-l)時(shí),其加1操作的結(jié)果是指向向量的下界0。
由于入隊(duì)時(shí)尾指針向前追趕頭指針,出隊(duì)時(shí)頭指針向前追趕尾指針,故隊(duì)空和隊(duì)滿時(shí)頭尾指針均相等。因此,我們無(wú)法通過(guò)Front=Rear來(lái)判斷隊(duì)列是空還是滿。在實(shí)際使用循環(huán)隊(duì)列時(shí),為了能區(qū)分隊(duì)列滿還是隊(duì)列空,通常還需增加一個(gè)標(biāo)志值,其定義如下:當(dāng)s=0時(shí)表示隊(duì)列空,當(dāng)s=1時(shí)表示隊(duì)列非空。
入隊(duì)運(yùn)算:入隊(duì)運(yùn)算是指在循環(huán)隊(duì)列的隊(duì)尾加入一個(gè)新元素。首先將隊(duì)尾指針進(jìn)1(即Rear=Rear+1),且當(dāng)Rear=m+l時(shí)置Rear=1;然后將新元素插入到隊(duì)尾指針指向的位置。當(dāng)循環(huán)隊(duì)列非空(s=l)且隊(duì)尾指針等于隊(duì)頭指針時(shí),說(shuō)明循環(huán)隊(duì)列已滿,不能進(jìn)行入隊(duì)運(yùn)算,這種情況稱為“上溢”。
出隊(duì)運(yùn)算:出隊(duì)運(yùn)算是指在循環(huán)隊(duì)列的隊(duì)頭位置退出一個(gè)元素并賦給指定的變量。首先將隊(duì)頭指針進(jìn)1(即From=Front+1),且當(dāng)Front=m+1時(shí)置Front=1,然后將排頭指針指向的元素賦給指定的變量。當(dāng)循環(huán)隊(duì)列為空(s=0)時(shí),不能進(jìn)行出隊(duì)運(yùn)算,這種情況稱為“下溢”。
1.1.4 線性鏈表
本節(jié)主要考查線性鏈表的存儲(chǔ)方式和基本操作。
1.線性表的鏈?zhǔn)酱鎯?chǔ)
在定義的鏈表中,若只含有一個(gè)指針域來(lái)存放下一個(gè)元素地址,稱這樣的鏈表為單鏈表或線性鏈表,如圖1-4所示。

圖1-4 線性表鏈?zhǔn)酱鎯?chǔ)
在鏈?zhǔn)酱鎯?chǔ)方式中,要求每個(gè)節(jié)點(diǎn)由兩部分組成:一部分用于存放數(shù)據(jù)元素值,稱為數(shù)據(jù)域;另一部分用于存放指針,稱為指針域。其中指針用于指向該節(jié)點(diǎn)的前一個(gè)或后一個(gè)節(jié)點(diǎn)(即前件節(jié)點(diǎn)或后件節(jié)點(diǎn))。
(1)線性鏈表的存儲(chǔ)結(jié)構(gòu)
用一組任意的存儲(chǔ)單元來(lái)依次存放線性表的節(jié)點(diǎn),這組存儲(chǔ)單元既可以是連續(xù)的,也可以是不連續(xù)的,甚至可以是零散分布在內(nèi)存中的任意位置上的。因此,鏈表中節(jié)點(diǎn)的邏輯次序和物理次序不一定相同。為了能正確表示節(jié)點(diǎn)間的邏輯關(guān)系,在存儲(chǔ)每個(gè)節(jié)點(diǎn)值的同時(shí),還必須存儲(chǔ)指示其后件節(jié)點(diǎn)的地址(或位置)信息,這個(gè)信息稱為指針(Pointer)或鏈(Link)。這兩部分組成了鏈表中的節(jié)點(diǎn)結(jié)構(gòu),鏈表正是通過(guò)每個(gè)節(jié)點(diǎn)的鏈域?qū)⒕€性表的n個(gè)節(jié)點(diǎn)按其邏輯次序鏈接在一起。由于上述鏈表的每一個(gè)節(jié)點(diǎn)只有一個(gè)鏈域,故將這種鏈表稱為單鏈表(Single Linked)。
顯然,單鏈表中每個(gè)節(jié)點(diǎn)的存儲(chǔ)地址存放在其前驅(qū)節(jié)點(diǎn)Next域中,而開始節(jié)點(diǎn)無(wú)前驅(qū)節(jié)點(diǎn),故應(yīng)設(shè)頭指針HEAD指向開始節(jié)點(diǎn)。同時(shí),由于終端節(jié)點(diǎn)無(wú)后繼節(jié)點(diǎn),故終端節(jié)點(diǎn)的指針域?yàn)榭眨碞ULL。
(2)線性鏈表的基本運(yùn)算
線性鏈表的基本運(yùn)算包括在線性鏈表中查找指定元素、在線性鏈表中插入元素、在線性鏈表中刪除元素。
1)在線性鏈表中查找指定元素:在對(duì)線性鏈表進(jìn)行插入或刪除的運(yùn)算中,總是首先需要找到插入或刪除的位置,這就需要對(duì)線性鏈表進(jìn)行掃描查找,在線性鏈表中尋找包含指定元素的前一個(gè)節(jié)點(diǎn)。
在鏈表中,查找是否有節(jié)點(diǎn)值等于給定值x的節(jié)點(diǎn),若有的話,則返回首次找到的其值為x的節(jié)點(diǎn)的存儲(chǔ)位置;否則返回NULL。查找過(guò)程從開始節(jié)點(diǎn)出發(fā),順著鏈表逐個(gè)將節(jié)點(diǎn)的值與給定值x做比較。
2)在線性鏈表中插入元素:線性鏈表的插入是指在鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu)下的線性鏈表中插入一個(gè)新元素。
插入運(yùn)算是將值為x的新節(jié)點(diǎn)插入到表的第i-1個(gè)節(jié)點(diǎn)和第i個(gè)節(jié)點(diǎn)之間。因此,必須首先找到ai-1的存儲(chǔ)位置p,然后生成一個(gè)數(shù)據(jù)域?yàn)閤的新節(jié)點(diǎn)*p,并令節(jié)點(diǎn)p的指針域指向新節(jié)點(diǎn),新節(jié)點(diǎn)的指針域指向節(jié)點(diǎn)ai。
由線性鏈表的插入過(guò)程可以看出,由于插入的新節(jié)點(diǎn)取自于可利用棧,因此,只要可利用棧不空,在線性鏈表插入時(shí)總能取到存儲(chǔ)插入元素的新節(jié)點(diǎn),不會(huì)發(fā)生“上溢”的情況。而且,由于可利用棧是公用的,多個(gè)線性鏈表可以共享它,從而可很方便地實(shí)現(xiàn)存儲(chǔ)空間的動(dòng)態(tài)分配。另外,線性鏈表在插入過(guò)程中不發(fā)生數(shù)據(jù)元素移動(dòng)的現(xiàn)象,只要改變有關(guān)節(jié)點(diǎn)的指針即可,從而提高了插入的效率。
3)在線性鏈表中刪除元素:線性鏈表的刪除是指在鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu)下的線性鏈表中刪除包含指定元素的節(jié)點(diǎn)。
刪除運(yùn)算是將表的第i個(gè)節(jié)點(diǎn)刪去。因?yàn)樵趩捂湵碇泄?jié)點(diǎn)a的存儲(chǔ)地址是在其直接前驅(qū)節(jié)點(diǎn)ai-1的指針域Next中,所以必須先找到ai-1的存儲(chǔ)位置p,然后令p-﹥Next指向ai的直接后繼節(jié)點(diǎn),即把a(bǔ)i從鏈上摘下,最后釋放節(jié)點(diǎn)ai的空間。
從線性鏈表的刪除過(guò)程可以看出,從線性鏈表中刪除一個(gè)元素后,不需要移動(dòng)表中的數(shù)據(jù)元素,只要改變被刪除元素所在節(jié)點(diǎn)的前驅(qū)節(jié)點(diǎn)的指針域即可。另外,可利用棧收集計(jì)算機(jī)中所有的空閑節(jié)點(diǎn),當(dāng)從線性鏈表中刪除一個(gè)元素后,該元素的存儲(chǔ)節(jié)點(diǎn)就變?yōu)榭臻e,應(yīng)將空閑節(jié)點(diǎn)送回到可利用棧。
2.雙向鏈表的結(jié)構(gòu)及其基本運(yùn)算
雙向鏈表也叫雙鏈表,是鏈表的一種,它的每個(gè)數(shù)據(jù)節(jié)點(diǎn)中都有兩個(gè)指針,分別指向直接后繼節(jié)點(diǎn)和直接前驅(qū)節(jié)點(diǎn),如圖1-5所示。所以,從雙向鏈表中的任意一個(gè)節(jié)點(diǎn)開始,都可以很方便地訪問(wèn)它的前驅(qū)節(jié)點(diǎn)和后繼節(jié)點(diǎn)。

圖1-5 雙向鏈表
(1)雙向鏈表的基本運(yùn)算
1)插入:在雙向鏈表的第i個(gè)元素前插入一個(gè)新節(jié)點(diǎn)的時(shí)候,首先,找到待插入的位置,用指針p指向該節(jié)點(diǎn);然后,將新節(jié)點(diǎn)的前驅(qū)指針指向p節(jié)點(diǎn)的前一個(gè)節(jié)點(diǎn);之后,將p節(jié)點(diǎn)的前一個(gè)節(jié)點(diǎn)的后驅(qū)指針指向新的節(jié)點(diǎn);接下來(lái),將新節(jié)點(diǎn)的后驅(qū)指針指向p節(jié)點(diǎn);最后,將p節(jié)點(diǎn)的前驅(qū)指針指向新節(jié)點(diǎn)。
2)刪除:在雙向鏈表中刪除一個(gè)節(jié)點(diǎn)時(shí),可用指針p指向該節(jié)點(diǎn)。首先,將p節(jié)點(diǎn)的前一個(gè)節(jié)點(diǎn)的Next指向p節(jié)點(diǎn)的下一個(gè)節(jié)點(diǎn);然后,將p的下一個(gè)節(jié)點(diǎn)的前驅(qū)指針指向p的上一個(gè)節(jié)點(diǎn)。
(2)雙鏈表的結(jié)構(gòu)及其基本運(yùn)算
在前面所討論的線性鏈表中,其插入與刪除的運(yùn)算雖然比較方便,但還存在一個(gè)問(wèn)題,在運(yùn)算過(guò)程中對(duì)于空表和對(duì)第一個(gè)節(jié)點(diǎn)的處理必須單獨(dú)考慮,使空表與非空表的運(yùn)算不統(tǒng)一。
因此,可以考慮建立這樣的鏈表,具有單鏈表的特征,但又不需要增加額外的存儲(chǔ)空間,僅對(duì)表的鏈接方式稍做改變,使得對(duì)表的處理更加方便靈活。從單鏈表可知,最后一個(gè)節(jié)點(diǎn)的指針域?yàn)镹ULL,表示單鏈表已經(jīng)結(jié)束。如果將單鏈表最后一個(gè)節(jié)點(diǎn)的指針域改為存放鏈表中頭節(jié)點(diǎn)(或第一個(gè)節(jié)點(diǎn))的地址,就使得整個(gè)鏈表構(gòu)成一個(gè)環(huán),又沒有增加額外的存儲(chǔ)空間,而滿足這樣條件的鏈表叫循環(huán)鏈表。
循環(huán)鏈表具有以下兩個(gè)特點(diǎn):
1)在循環(huán)鏈表中增加了一個(gè)表頭節(jié)點(diǎn),其數(shù)據(jù)域?yàn)槿我饣蛘吒鶕?jù)需要來(lái)設(shè)置,指針域指向線性表的第一個(gè)元素的節(jié)點(diǎn)。循環(huán)鏈表的頭指針指向表頭節(jié)點(diǎn)。
2)循環(huán)鏈表中最后一個(gè)節(jié)點(diǎn)的指針域不是空,而是指向表頭節(jié)點(diǎn)。即在循環(huán)鏈表中,所有節(jié)點(diǎn)的指針構(gòu)成了一個(gè)環(huán)狀鏈。
在循環(huán)鏈表中,只要指出表中任何一個(gè)節(jié)點(diǎn)的位置,就可以從它出發(fā)訪問(wèn)到表中其他所有的節(jié)點(diǎn),而線性單鏈表做不到這一點(diǎn)。
由于在循環(huán)鏈表中設(shè)置了一個(gè)表頭節(jié)點(diǎn),因此,在任何情況下,循環(huán)鏈表中至少有一個(gè)節(jié)點(diǎn)存在,從而使空表的運(yùn)算與非空表統(tǒng)一。
1.1.5 樹與二叉樹
本節(jié)要求考生掌握樹和二叉樹的基本定義,重點(diǎn)考查二叉樹的基本性質(zhì)和二叉樹的遍歷。
1.樹的定義
樹是由n(n≥0)個(gè)節(jié)點(diǎn)組成的有限集合。若n=0,稱為空樹;若n>0,則:
1)有一個(gè)特定的稱為根(Root)的節(jié)點(diǎn)。它只有直接后繼節(jié)點(diǎn),而沒有直接前驅(qū)節(jié)點(diǎn)。
2)除根節(jié)點(diǎn)以外的其他節(jié)點(diǎn)可以劃分為m(m≥0)個(gè)互不相交的有限集合T0,T1,…,Tm-1,每個(gè)集合Ti(i=0,1,…,m-l)又是一棵樹,稱為根的子樹;每棵子樹的根節(jié)點(diǎn)有且僅有一個(gè)直接前驅(qū)節(jié)點(diǎn),但可以有0個(gè)或多個(gè)直接后繼節(jié)點(diǎn)。
如圖1-6所示是一棵樹的示例。
2.二叉樹的定義及其性質(zhì)
二叉樹(Binary Tree)是由n(n≥0)個(gè)節(jié)點(diǎn)的有限集合構(gòu)成,此集合或者為空集,或者由一個(gè)根節(jié)點(diǎn)及兩棵互不相交的左右子樹組成,并且左右子樹都是二叉樹,如圖1-7所示。二叉樹可以是空集合,根可以有空的左子樹或空的右子樹。
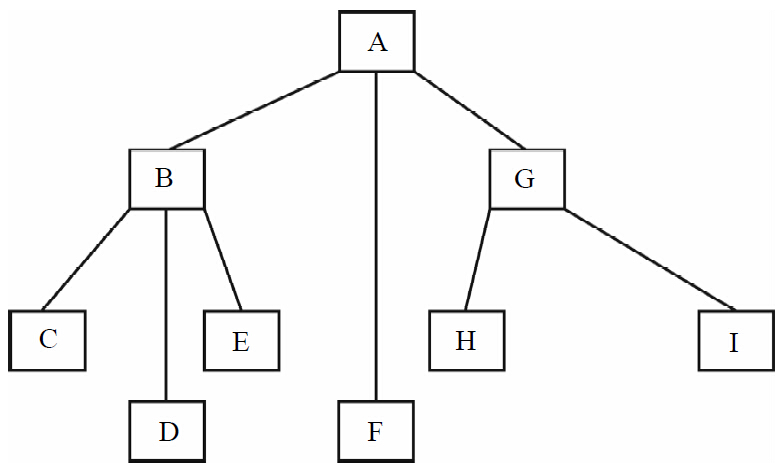
圖1-6 樹的示例
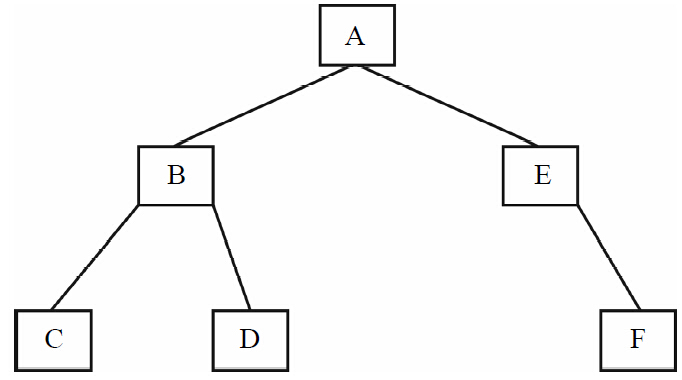
圖1-7 二叉樹
(1)二叉樹的特點(diǎn)
二叉樹具有以下兩個(gè)特點(diǎn):
1)非空二叉樹只有一個(gè)根節(jié)點(diǎn)。
2)每一個(gè)節(jié)點(diǎn)最多有兩棵子樹,且分別稱為該節(jié)點(diǎn)的左子樹和右子樹。
在二叉樹中,一個(gè)節(jié)點(diǎn)可以只有左子樹而沒有右子樹,也可以只有右子樹而沒有左子樹。當(dāng)一個(gè)節(jié)點(diǎn)既沒有左子樹也沒有右子樹時(shí),該節(jié)點(diǎn)即為葉子節(jié)點(diǎn)。
(2)滿二叉樹與完全二叉樹
1)滿二叉樹:除最后一層外,每一層上的所有節(jié)點(diǎn)都有兩個(gè)子節(jié)點(diǎn),如圖1-8所示。
2)完全二叉樹:除最后一層外,每一層上的節(jié)點(diǎn)數(shù)均達(dá)到最大值;在最后一層上只缺少右邊的若干節(jié)點(diǎn),如圖1-9所示。
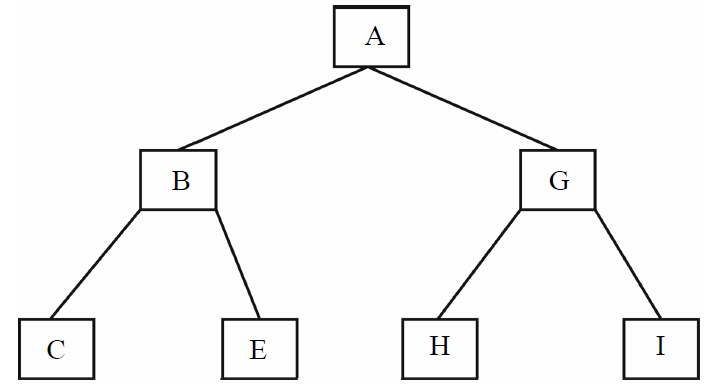
圖1-8 滿二叉樹
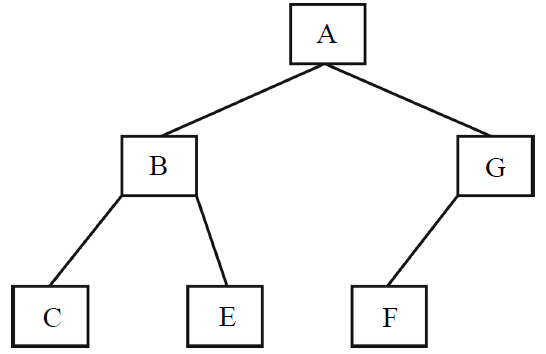
圖1-9 完全二叉樹
如果有一棵具有n個(gè)節(jié)點(diǎn)的深度為k的完全二叉樹,則它的每一個(gè)節(jié)點(diǎn)都與深度為k的滿二叉樹中編號(hào)為1~n的節(jié)點(diǎn)一一對(duì)應(yīng)。
(3)二叉樹的基本性質(zhì)
性質(zhì)1:在二叉樹的第k層上至多有2 k-1個(gè)節(jié)點(diǎn)(k≥1)。
性質(zhì)2:深度為m的二叉樹至多有2 m-1個(gè)節(jié)點(diǎn)。
性質(zhì)3:對(duì)任何一棵二叉樹,度為0的節(jié)點(diǎn)(即葉子節(jié)點(diǎn))總是比度為2的節(jié)點(diǎn)多一個(gè)。
性質(zhì)4:具有n個(gè)節(jié)點(diǎn)的完全二叉樹的深度至少為【log2n】+1,其中【log2n】表示log2n的整數(shù)部分。
性質(zhì)5:具有n個(gè)節(jié)點(diǎn)的完全二叉樹深度為【log2n】+1或【log2(n+1)】。
性質(zhì)6:如果對(duì)一棵有n個(gè)節(jié)點(diǎn)的完全二叉樹的節(jié)點(diǎn)按層序編號(hào)(從第1層到第【log2n】+1層,每層從左到右),則對(duì)任一節(jié)點(diǎn)i(1≤i≤n)有:
1)如果i=1,則節(jié)點(diǎn)i無(wú)雙親,是二叉樹的根;如果i﹥1,則其雙親是節(jié)點(diǎn)【i/2】。
2)如果2i≤n,則節(jié)點(diǎn)i為葉子節(jié)點(diǎn),無(wú)左孩子;否則,其左孩子是節(jié)點(diǎn)2i。
3)如果2i+1≤n,則節(jié)點(diǎn)i無(wú)右孩子;否則,其右孩子是節(jié)點(diǎn)2i+1。
(4)二叉樹的存儲(chǔ)結(jié)構(gòu)
在計(jì)算機(jī)中,二叉樹通常采用鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu)。用于存儲(chǔ)二叉樹中各元素的存儲(chǔ)節(jié)點(diǎn)由兩部分組成:數(shù)據(jù)域與指針域。但在二叉樹中,由于每一個(gè)元素可以有兩個(gè)后繼節(jié)點(diǎn)(兩個(gè)子節(jié)點(diǎn)),因此,用于存儲(chǔ)二叉樹的存儲(chǔ)節(jié)點(diǎn)的指針域有兩個(gè):一個(gè)用于指向該節(jié)點(diǎn)的左子節(jié)點(diǎn)的存儲(chǔ)地址,稱為左指針域;另一個(gè)用于指向該節(jié)點(diǎn)的右子節(jié)點(diǎn)的存儲(chǔ)地址,稱為右指針域。
3.二叉樹的遍歷
所謂遍歷二叉樹,就是遵從某種次序,訪問(wèn)二叉樹中的所有節(jié)點(diǎn),使得每個(gè)節(jié)點(diǎn)僅被訪問(wèn)一次。
(1)前序遍歷
前序遍歷是指在訪問(wèn)根節(jié)點(diǎn)、遍歷左子樹與遍歷右子樹這三者中,首先訪問(wèn)根節(jié)點(diǎn),然后遍歷左子樹,最后遍歷右子樹;并且,在遍歷左右子樹時(shí),仍然先訪問(wèn)根節(jié)點(diǎn),然后遍歷左子樹,最后遍歷右子樹。圖1-10中的二叉樹,前序遍歷序列:ABCDEF。
(2)中序遍歷
中序遍歷是指在訪問(wèn)根節(jié)點(diǎn)、遍歷左子樹與遍歷右子樹這三者中,首先遍歷左子樹,然后訪問(wèn)根節(jié)點(diǎn),最后遍歷右子樹;并且,在遍歷左、右子樹時(shí),仍然先遍歷左子樹,然后訪問(wèn)根節(jié)點(diǎn),最后遍歷右子樹。圖1-10中的二叉樹,中序遍歷序列:CBDAEF。
(3)后序遍歷
后序遍歷是指在訪問(wèn)根節(jié)點(diǎn)、遍歷左子樹與遍歷右子樹這三者中,首先遍歷左子樹,然后遍歷右子樹,最后訪問(wèn)根節(jié)點(diǎn);并且,在遍歷左、右子樹時(shí),仍然先遍歷左子樹,然后遍歷右子樹,最后訪問(wèn)根節(jié)點(diǎn)。圖1-10中的二叉樹,后序遍歷序列:CDBFEA。
例,已知二叉樹的中序遍歷序列為ABCDEFG,后序遍歷序列為BDCAFGE,則前序遍歷序列是什么?
解題過(guò)程如下:
1)從后序中,可以先得到根節(jié)點(diǎn)是E,然后再看中序的序列:ABCDEFG,可以發(fā)現(xiàn)ABCD位于根節(jié)點(diǎn)的左邊,而FG位于根節(jié)點(diǎn)的右邊,于是得到圖1-11所示的圖形。
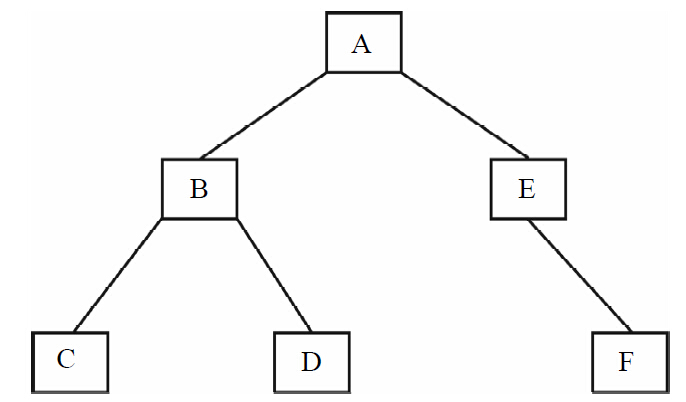
圖1-10 二叉樹的遍歷
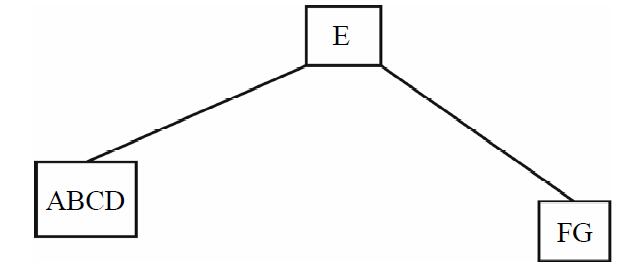
圖1-11 步驟一的圖形
2)先來(lái)看ABCD這部分,然后看后序序列,在后序序列中有BDCA這一部分,可以確定A是這部分的根,再看中序序列中的ABCD,發(fā)現(xiàn)BCD都在A的后面。因此,可以畫出如圖1-12所示的圖形。
3)再看BCD這部分,從后序中看到的順序是BDC,所以C是這部分的根節(jié)點(diǎn),中序序列是BCD,可以斷定B在C的左邊,D在C的右邊。這樣,得到如圖1-13所示的圖形。
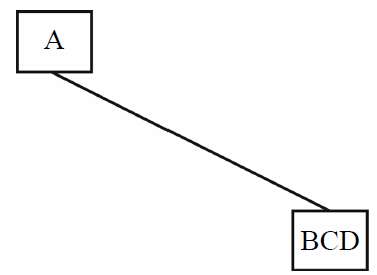
圖1-12 步驟二的圖形
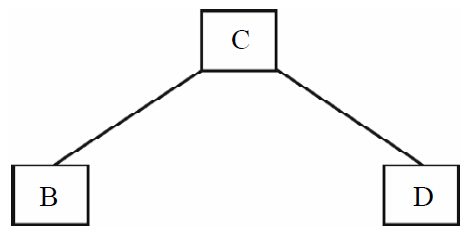
圖1-13 步驟三的圖形
4)再看看右邊的FG這部分,從后序序列FG和中序FG中,可以推出,G是這部分的根節(jié)點(diǎn),而F位于G的左邊。得到如圖1-14所示的圖形。
5)根據(jù)以上步驟合成一個(gè)二叉樹,如圖1-15所示。
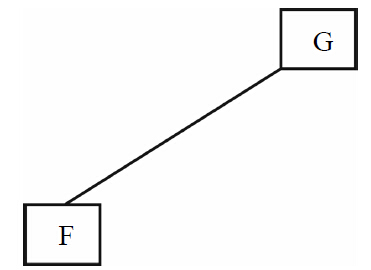
圖1-14 步驟四的圖形
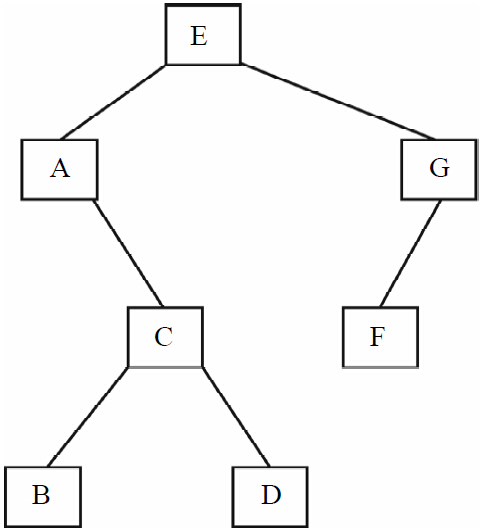
圖1-15 最后的二叉樹
6)寫出前序遍歷序列:EACBDGF。
1.1.6 查找技術(shù)
所謂查找是指在一個(gè)給定的數(shù)據(jù)結(jié)構(gòu)中查找某個(gè)指定的元素。在查找的過(guò)程中,涉及查找的方法等問(wèn)題,通常,根據(jù)不同的數(shù)據(jù)結(jié)構(gòu),應(yīng)采用不同的查找方法。
1.順序查找
順序查找又稱順序搜索。順序查找一般是指在線性表中查找指定的元素,其基本方法如下:
從線性表的第一個(gè)元素開始,依次將線性表中的元素與被查元素進(jìn)行比較,若相等則表示找到(即查找成功);若線性表中所有的元素與被查元素進(jìn)行了比較但都不相等,則表示線性表中沒有要找的元素(即查找失敗)。
在進(jìn)行順序查找過(guò)程中,如果線性表中的第一個(gè)元素就是被查找元素,則只需做一次比較即可查找成功,查找效率最高;但如果被查找的元素是線性表中的最后一個(gè)元素,或者被查元素根本不在線性表中,則為了查找這個(gè)元素需要與線性表中所有的元素進(jìn)行比較,這是順序查找的最壞情況。在平均情況下,利用順序查找法在線性表中查找一個(gè)元素,大約要與線性表中一半的元素進(jìn)行比較。
由此可以看出,對(duì)于大的線性表來(lái)說(shuō),順序查找的效率是很低的。雖然順序查找的效率不高,但在下列兩種情況下也只能采用順序查找。
1)如果線性表為無(wú)序線性表(即表中元素的排列是無(wú)序的),則不管是順序存儲(chǔ)結(jié)構(gòu)還是鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu),都只能用順序查找。
2)即使是有序線性表,如果線性表采用鏈?zhǔn)酱鎯?chǔ)結(jié)構(gòu),也只能用順序查找。
2.二分法查找
二分法查找只適用于順序存儲(chǔ)的有序表。在此所說(shuō)的有序表是指線性表中的元素按值非遞減排列(即從小到大,但允許相鄰元素值相等)。
設(shè)有序線性表的長(zhǎng)度為n,被查元素為x,則二分查找的方法如下。
將x與線性表的中間項(xiàng)進(jìn)行比較。
1)若中間項(xiàng)的值等于x,則說(shuō)明查找成功,查找結(jié)束。
2)若x小于中間項(xiàng)的值,則在線性表的前半部分(即中間項(xiàng)以前的部分)以相同的方法進(jìn)行查找。
3)若x大于中間項(xiàng)的值,則在線性表的后半部分(即中間項(xiàng)以后的部分)以相同的方法進(jìn)行查找。
這個(gè)過(guò)程一直進(jìn)行到查找成功或子表長(zhǎng)度為0(說(shuō)明線性表中沒有這個(gè)元素)為止。
1.1.7 排序技術(shù)
在排序技術(shù)方面,主要考查插入排序、選擇排序、冒泡排序、快速排序和堆排序等方法。
1.插入排序
每次將一個(gè)待排序的數(shù)據(jù)元素插入到前面已經(jīng)排好序的數(shù)列中的適當(dāng)位置,使數(shù)列依然有序,直到待排序數(shù)據(jù)元素全部插入完為止。
例,使用插入排序?qū)?、4、2、1、5按照從小到大的順序排序。
排序過(guò)程分析:
第一趟3 4 2 1 5
第二趟2 3 4 1 5
第三趟1 2 3 4 5
第四趟1 2 3 45
2.選擇排序
每一趟從待排序的數(shù)據(jù)元素中選出最小(或最大)的一個(gè)元素,順序放在已排好序的數(shù)列的最前,直到全部待排序的數(shù)據(jù)元素排完。
例,使用選擇排序?qū)?、4、2、1、5按照從小到大的順序排序。
排序過(guò)程分析:
第一趟1 4 2 3 5
第二趟 1 2 4 3 5
第三趟1 2 34 5
第四趟1 2 3 4 5
3.冒泡排序
兩兩比較待排序數(shù)據(jù)元素的大小,發(fā)現(xiàn)兩個(gè)數(shù)據(jù)元素的次序相反時(shí)即進(jìn)行交換,直到?jīng)]有反序的數(shù)據(jù)元素為止。
設(shè)想被排序的數(shù)組R[1..N]垂直豎立,將每個(gè)數(shù)據(jù)元素看成有重量的氣泡,根據(jù)輕氣泡不能在重氣泡之下的原則,從下往上掃描數(shù)組R,凡掃描到違反本原則的輕氣泡,就使其向上“漂浮”,如此反復(fù)進(jìn)行,直至最后任何兩個(gè)氣泡都是輕者在上、重者在下為止。
例,使用冒泡排序?qū)?、4、2、1、5按照從小到大的順序排序。
排序過(guò)程分析:
第一趟 3 2 1 4 5
第二趟 2 1 3 4 5
第三趟 1 2 3 4 5
第四趟 1 2 3 4 5
4.快速排序
在當(dāng)前無(wú)序區(qū)R[1..H]中任取一個(gè)數(shù)據(jù)元素作為比較的“基準(zhǔn)”(不妨記為X),用此基準(zhǔn)將當(dāng)前無(wú)序區(qū)劃分為左右兩個(gè)較小的無(wú)序區(qū):R[1..I-1]和R[I+1..H],且左邊的無(wú)序子區(qū)中數(shù)據(jù)元素均小于等于基準(zhǔn)元素,右邊的無(wú)序子區(qū)中數(shù)據(jù)元素均大于等于基準(zhǔn)元素,而基準(zhǔn)X則位于最終排序的位置上,即R[1..I-1]≤X.Key≤R[I+1..H](1≤I≤H),當(dāng)R[1..I-1]和R[I+1..H]均非空時(shí),分別對(duì)它們進(jìn)行上述的劃分過(guò)程,直至所有無(wú)序子區(qū)中的數(shù)據(jù)元素均已排序?yàn)橹埂?/p>
例如,使用快速排序?qū)?、8、3、4、9、1進(jìn)行從小到大的排序(僅寫出第一趟的結(jié)果,以第一個(gè)元素為主)。
排序過(guò)程分析:
第一趟 7 8 3 4 9 1
第二趟 1 8 3 4 9 7
第三趟 1 7 3 4 9 8
第四趟 1 4 3 7 9 8
第五趟 1 4 3 7 9 8
一般來(lái)說(shuō),在考試的時(shí)候,只問(wèn)第一趟的結(jié)果,也就是以第一個(gè)元素為主排列的結(jié)果。
5.堆排序
堆排序是一樹形選擇排序,在排序過(guò)程中,將R[1..N]看成是一棵完全二叉樹的順序存儲(chǔ)結(jié)構(gòu),利用完全二叉樹中雙親節(jié)點(diǎn)和孩子節(jié)點(diǎn)之間的內(nèi)在關(guān)系來(lái)選擇最小的元素。
N個(gè)元素的序列K1,K2,K3,…,KN稱為堆,當(dāng)且僅當(dāng)該序列滿足以下特性:
Ki≤K2i,Ki≤K2i+1(1≤i≤[N/2])
堆實(shí)質(zhì)上是滿足如下性質(zhì)的完全二叉樹:樹中任一非葉子節(jié)點(diǎn)的關(guān)鍵字均大于等于其孩子節(jié)點(diǎn)的關(guān)鍵字。
堆排序正是利用小根堆(或大根堆)來(lái)選取當(dāng)前無(wú)序區(qū)中關(guān)鍵字最小(或最大)的記錄實(shí)現(xiàn)排序的。我們不妨利用大根堆來(lái)排序。每一趟排序的基本操作是:將當(dāng)前無(wú)序區(qū)調(diào)整為一個(gè)大根堆,選取關(guān)鍵字最大的堆頂記錄,將它和無(wú)序區(qū)中的最后一個(gè)記錄交換。這樣,正好和直接選擇排序相反,有序區(qū)是在原記錄區(qū)的尾部形成并逐步向前擴(kuò)大到整個(gè)記錄區(qū)。
例如,使用堆排序?qū)?、8、3、4、9、1進(jìn)行從小到大的排序,僅寫出第一趟排序的結(jié)果。
排序過(guò)程分析:

因?yàn)橛?個(gè)數(shù),首先取6/2=3,然后看看k3≤k6是否成立(此處沒有k7),因?yàn)閗3的值是3,而k6的值是1,顯然不滿足條件,要將k3和k6進(jìn)行交換,就變成如下形式:

然后再看k2≤k4和k2≤k5是否成立。因?yàn)閗2的值是8,k4的值是4,而k5的值是9,所以,將k2的值和k4的值交換,得到如下序列:

再看k1≤k2和k1≤k3,發(fā)現(xiàn)不滿足,此時(shí)的k1要和k2與k3中最小的一個(gè)進(jìn)行交換,所以得到序列如下:

堆建好了嗎?檢查每個(gè)位置是否滿足上面的條件,答案是“沒有”。因?yàn)榇藭r(shí)k3≤k6又不成立了,所以要進(jìn)行交換,得到如下的序列:

以上是第一趟排列的結(jié)果,如果要進(jìn)行第二趟堆排序的話,就從剩下的4、3、8、9、7開始。
6.各種排序方法的比較
各種排序方法的比較如表1-1所示。
表1-1 各種排序算法的比較

- 2019年11月全國(guó)計(jì)算機(jī)技術(shù)與軟件專業(yè)技術(shù)資格(水平)考試《系統(tǒng)集成項(xiàng)目管理工程師(中級(jí))》復(fù)習(xí)全書【核心講義+歷年真題詳解】
- 全國(guó)職稱計(jì)算機(jī)考試講義·真題·預(yù)測(cè)三合一:中文Windows XP操作系統(tǒng)
- 全國(guó)計(jì)算機(jī)等級(jí)考試歷年真題與機(jī)考題庫(kù):二級(jí)MS Office高級(jí)應(yīng)用
- 全國(guó)計(jì)算機(jī)等級(jí)考試真題匯編與專用題庫(kù):二級(jí)Access
- 2013全國(guó)計(jì)算機(jī)等級(jí)考試新版無(wú)紙化上機(jī)考試臨考沖刺模擬實(shí)戰(zhàn):二級(jí)Access數(shù)據(jù)庫(kù)
- 2020年3月全國(guó)計(jì)算機(jī)等級(jí)考試《四級(jí)軟件工程》復(fù)習(xí)全書【核心講義+歷年真題詳解】
- 全國(guó)計(jì)算機(jī)等級(jí)考試一本通:一級(jí)計(jì)算機(jī)基礎(chǔ)及MS Office應(yīng)用
- 全國(guó)職稱計(jì)算機(jī)考試標(biāo)準(zhǔn)教材與專用題庫(kù):Excel 2003中文電子表格
- 2014年全國(guó)計(jì)算機(jī)等級(jí)考試3年真題精解與過(guò)關(guān)全真訓(xùn)練題:二級(jí)公共基礎(chǔ)知識(shí)
- 黑光造型:創(chuàng)意造型設(shè)計(jì)佳作賞析
- 2020年3月全國(guó)計(jì)算機(jī)等級(jí)考試《二級(jí)Visual Basic語(yǔ)言程序設(shè)計(jì)》【教材精講+真題解析】講義與視頻課程【46小時(shí)高清視頻】
- 全國(guó)職稱計(jì)算機(jī)考試標(biāo)準(zhǔn)教材與專用題庫(kù):PowerPoint 2007中文演示文稿
- 5天通過(guò)職稱計(jì)算機(jī)考試(考點(diǎn)視頻串講+全真模擬):Excel 2003中文電子表格(第2版) (全國(guó)專業(yè)技術(shù)人員計(jì)算機(jī)應(yīng)用能力考試指導(dǎo)叢書)
- 全國(guó)計(jì)算機(jī)等級(jí)考試《二級(jí)C語(yǔ)言程序設(shè)計(jì)》專用教材【考綱分析+考點(diǎn)精講+真題演練+強(qiáng)化習(xí)題】
- 5天通過(guò)職稱計(jì)算機(jī)考試(考點(diǎn)視頻串講+全真模擬):Word 2003中文字處理(第2版) (全國(guó)專業(yè)技術(shù)人員計(jì)算機(jī)應(yīng)用能力考試指導(dǎo)叢書)