- 財務管理實務（微課版·第4版）
- 周星煜 鄧燏主編
- 10397字
- 2025-08-06 17:29:44
任務實訓
資金時間價值的應用范圍很廣，涉及企業籌資、投資、營運等各個環節。資金時間價值的計算與應用形式主要分為三種：一是一次性收付款項的計算及應用，二是年金的計算及應用，三是混合現金流的計算及應用。混合現金流的計算及應用往往建立在前兩者的基礎之上，本任務實訓不作詳細介紹，感興趣的讀者可查閱相關資料學習。
一、一次性收付款項的計算及應用
一次性收付款項是指在某一特定時點上一次性支付（收取），經過一段時間后再相應地一次性收取（支付）的款項。在日常理財過程中，需要對一次性收付款項的現值或終值等指標進行計算，得出所需的相關指標，以做出科學的決策。一次性收付款項終值、現值的計算如圖1-2-1所示。
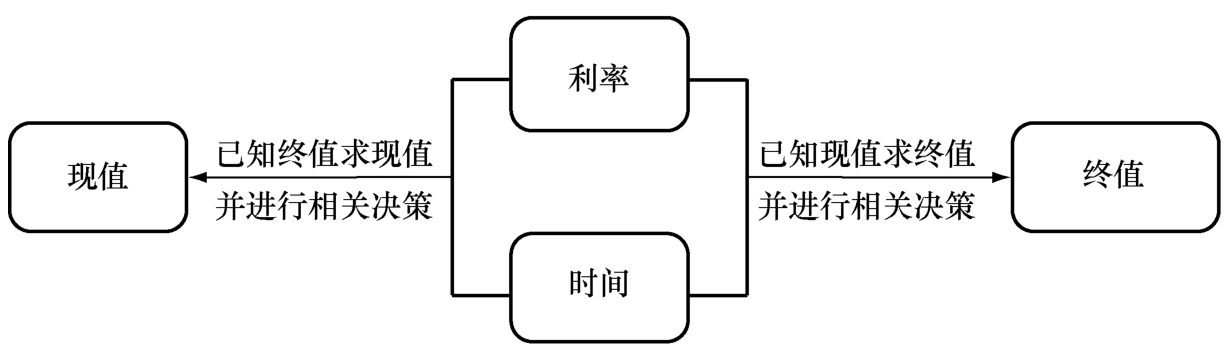
圖1-2-1 一次性收付款項終值、現值的計算
1.單利終值與現值的計算與應用
（1）單利終值的計算（已知現值求終值）。計算公式如下。
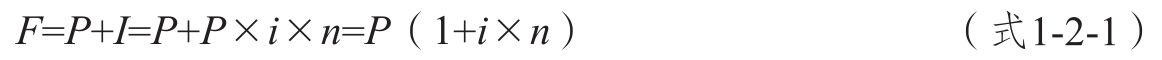
其中，F為終值，P為現值，I為利息，i為利率（折現率），n為計息期。
（2）單利現值的計算（已知終值求現值）。計算公式如下。
提示
單利終值系數和單利現值系數互為倒數。
【任務1-2-1】王先生現在有一筆資金10 000元，如果存進銀行做定期儲蓄存款，期限3年，年利率為3%，按單利計息，則到期時王先生所得的本利和為多少？
【解析】F=P（1+i×n）=10 000×（1+3%×3）=10 900（元）。
按照每年3%的單利計息，10 000元本金在3年內的利息為900元。如果按照單利計算，3年后的10 900元相當于現在的多少資金呢？這就是所謂的“現值”問題。
【任務1-2-2】張先生想在3年后從銀行取出10 900元，假設銀行當前的3年期存款年利率為3%，按單利計息，那么他現在應該存進多少元？
【解析】P=F/（1+i×n）=10 900/（1+3%×3）=10 000（元）。
隨堂練習
（1）甲企業向銀行借款30萬元，年利率為8%，期限為3年，按單利計息。3年后該企業應償還的本利和是多少？
（2）李某希望5年后能存夠60萬元，年利率為10%，按單利計息，那么他現在應該向銀行存入多少元？
2.復利終值與現值的計算與應用
（1）復利終值的計算（已知現值求終值）。復利的終值是一定量的本金按復利計算若干期后的本利和，如圖1-2-2所示。
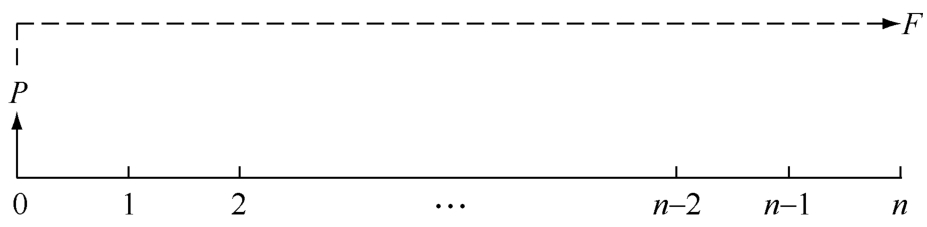
圖1-2-2 復利終值
計算公式如下。
式1-2-3中，（1+i）n為復利終值系數，用符號（F/P，i，n）表示，其值可查閱本書附錄中的復利終值系數表（見附表1）。
（2）復利現值的計算（已知終值求現值）。復利的現值是復利終值的逆運算，它是指未來某一特定時點收取（支付）的一筆款項按折現率所計算的現在的價值，如圖1-2-3所示。
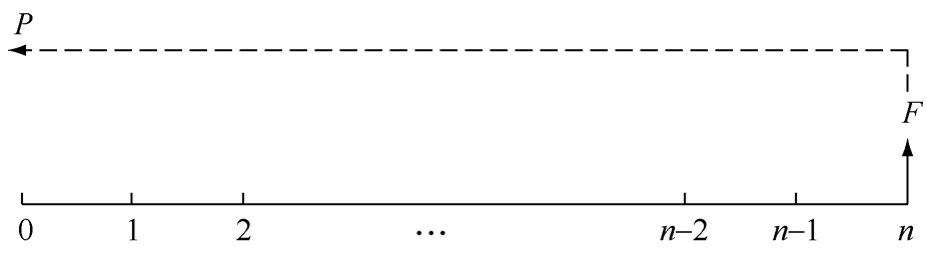
圖1-2-3 復利現值
計算公式如下。
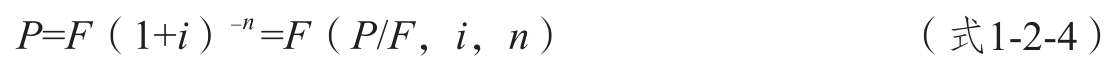
式1-2-4中，（1+i）-n為復利現值系數，用符號（P/F，i，n）表示，其值可查閱本書附錄中的復利現值系數表（見附表2）。
提示
復利終值系數和復利現值系數互為倒數。在財務管理中，一般按復利計息。
【任務1-2-3】王先生現在有一筆資金10 000元，如果存進銀行做定期儲蓄存款，期限3年，年利率為3%，則到期時王先生所得的本利和為多少？
【解析】F=P（F/P，i，n）=10 000×（F/P，3%，3）=10 000×1.092 7=10 927（元）。
【任務1-2-4】張先生想在5年后從銀行取出50 000元，假設銀行存款年利率為5%，那么他現在應該存入銀行多少元？
【解析】P=F（P/F，i，n）=50 000×（P/F，5%，5）=50 000×0.783 5=39 175（元）。
技能拓展 Excel在復利終值及現值計算中的應用
1.使用插入函數法計算復利終值
本法是指在Excel環境下，通過插入財務函數FV，并根據計算機系統的提示，正確輸入已知的現值pv、期限nper和折現率rate，從而直接求得終值FV的方法。
沿用【任務1-2-3】中的有關數據，利用插入函數法確定其終值，解析如下。
【解析】從已知條件可以看出，這是已知現值計算終值的問題，可以使用函數FV進行計算，其中參數pv為10 000，nper為3，rate為3%，其余參數可省略，如圖1-2-4所示。
Excel在復利終值及現值計算中的應用
在圖1-2-4所示的B5單元格中輸入公式“=FV（B4，B3，，-B2）”，即可得到3年后王先生所得的本利和為10 927.27元。
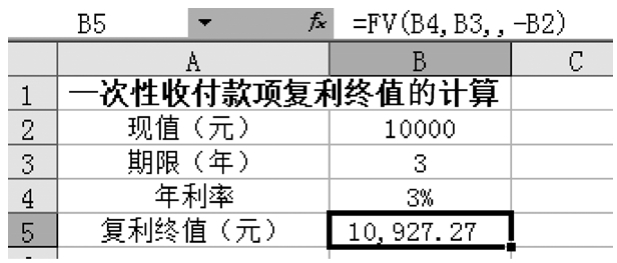
圖1-2-4 一次性收付款項復利終值的計算
2.使用插入函數法計算復利現值
本法是指在Excel環境下，通過插入財務函數PV，并根據計算機系統的提示，正確輸入已知的終值fv、期限nper和折現率rate，從而直接求得現值PV的方法。
沿用【任務1-2-4】中的有關數據，利用插入函數法確定其現值，解析如下。
【解析】從題意可知，這是已知終值計算現值的問題，可以使用函數PV進行計算，其中參數fv為50 000，nper為5，rate為5%，其余參數可省略，如圖1-2-5所示。
在圖1-2-5所示的B5單元格中輸入公式“=PV（B4，B3，，B2）”，就可以得出張先生現在應存入銀行39176.31元。
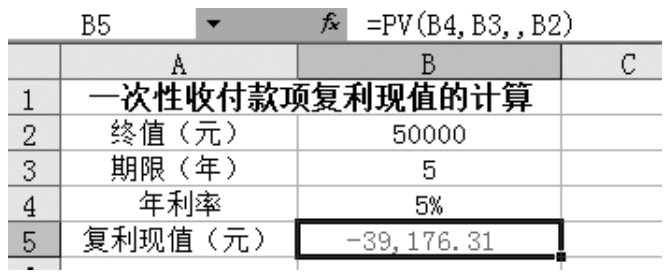
圖1-2-5 一次性收付款項復利現值的計算
提示
（1）財務函數一般可采用以下3種方法輸入。
①先將相關數據輸入Excel表格中，然后單擊【公式】選項卡中的【插入函數】按鈕，在彈出的【插入函數】對話框中，找到所需的財務函數，單擊【確定】按鈕，彈出【函數參數】對話框。單擊參數輸入文本框右側的折疊按鈕，然后選擇相關數據所在單元格，最后單擊【確定】按鈕。
②在【函數參數】對話框中直接輸入數據，這種方法一般用于只需要計算一個結果的情況。
③在單元格中直接輸入財務函數。這種方法需要記住函數名稱及其所使用的參數，要做到這點比較困難，所以并不常用。
（2）在本書所有的參數設置中，凡是投資（支出）的金額都以負數表示，收益（收入）的金額都以正數表示。
（3）因計算過程中保留小數位數不同，導致人工計算與Excel軟件計算的結果可能略有差異，后面不再說明。
隨堂練習
（1）某投資者在2022年向銀行存入一筆3萬元的款項，按復利計息，年利率為2%，則6年后得到多少本利和？
（2）劉先生擬購房，開發商提出兩個方案，甲方案是現在一次性支付80萬元，乙方案是5年后一次性支付100萬元，若銀行按揭貸款年利率為7%，問劉先生應如何付款？
知識鏈接 實際利率與名義利率的換算
當每年復利次數超過一次時，所給定的年利率稱為名義利率，也稱報價利率。而每年只復利一次的利率稱為實際利率，也稱有效年利率。每年復利次數為m，將名義利率r調整為實際利率i的換算公式如下。
【任務1-2-5】某企業向銀行借款30 000元，按季度計息，年利率為8%，則3年后這筆借款的終值為多少？
【解析】方法一，調整期數和利率。
F=P（F/P，i，n）=30 000×（F/P，8%/4，3×4）=30 000×1.268 2=38 046（元）。
方法二，按照實際利率計算（本書計算結果默認保留小數點后兩位數字，以下不再重復說明）。
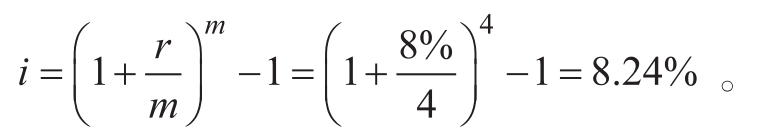
F=P（F/P，i，n）=30 000×（F/P，8.24%，3）=30 000×1.268 2=38 046（元）。
二、年金的計算及應用
在日常經濟活動中，資金除了存在一次性收付款項的情況，還存在分期等額系列收付款項的情況。年金是指在一定時期內每期發生的等額系列收付款項，通常用“A”表示。年金存在的形式多種多樣，主要表現為連續發生的等額利息、等額租金、等額保險費、等額分期收款、等額分期付款等。年金、現值或終值的計算關系如圖1-2-6所示。
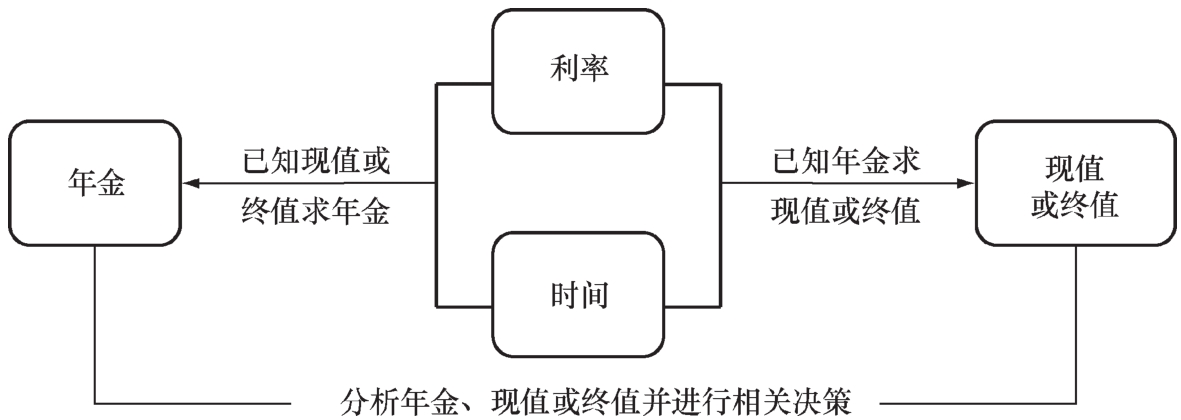
圖1-2-6 年金、現值或終值的計算關系
年金按其收付發生的時點不同，分為普通年金、預付年金、遞延年金、永續年金等。
1.普通年金終值和現值的計算
普通年金，又稱后付年金，是指一定時期內每期期末等額的系列收付款項。
提示
年金收付間隔期不一定是一年，可以是半年、一個季度、一個月等。
（1）普通年金終值的計算。普通年金終值猶如零存整取的本利和，它是一定時期內每期期末等額收付款項的復利終值之和，計算方法如圖1-2-7所示。
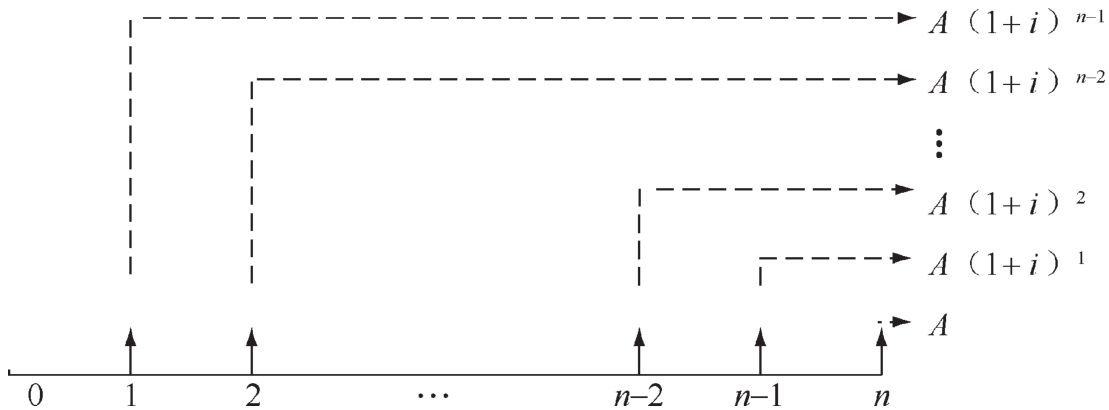
圖1-2-7 普通年金終值計算示意
普通年金終值的計算公式如下。
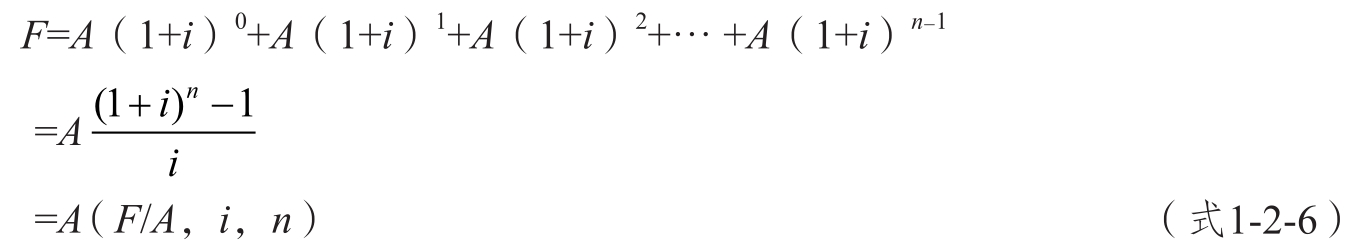
式1-2-6中，
為年金終值系數，用符號（F/A，i，n）表示，其值可查閱本書附錄中的年金終值系數表（見附表3）。
【任務1-2-6】李女士計劃每年年末存入銀行10 000元，共存10年，以便能在10年后退休時擁有一筆養老金，已知年利率為2%，請問李女士10年后可從銀行取出多少錢？
【解析】F=A（F/A，i，n）=10 000×（F/A，2%，10）=10 000×10.949 7=109 497（元）。
償債基金是指為了在約定的未來某一時點清償某筆債務或積累一定數額的資金而必須分次等額形成的存款準備金。簡單來說，就是為了在第n期期末償付或積累F，每期期末應該存入的金額A。
根據F=A（F/A，i，n），推導出A=F/（F/A，i，n）或A=F（A/F，i，n）。其中，（A/F，i，n）為償債基金系數，它與年金終值系數互為倒數。
【任務1-2-7】某人擬在5年后還清10 000元的債務，從現在起每年年末等額存入銀行一筆款項。假設銀行存款年利率為6%，則其每年需要存入多少元？
【解析】A=F/（F/A，i，n）=10 000/（F/A，6%，5）=10 000/5.637 1=1 773.96（元）。
（2）普通年金現值的計算。普通年金現值猶如整存零取的本金，它是一定時期內每期期末等額收付款項的復利現值之和。其計算方法如圖1-2-8所示。
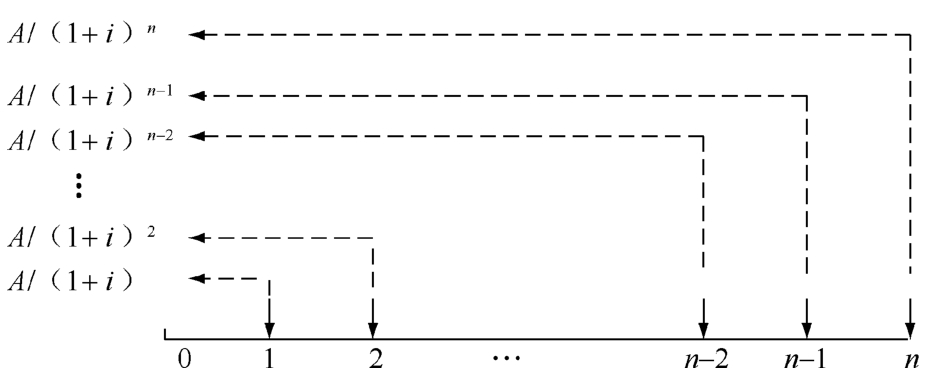
圖1-2-8 普通年金現值計算示意
普通年金現值的計算公式如下。
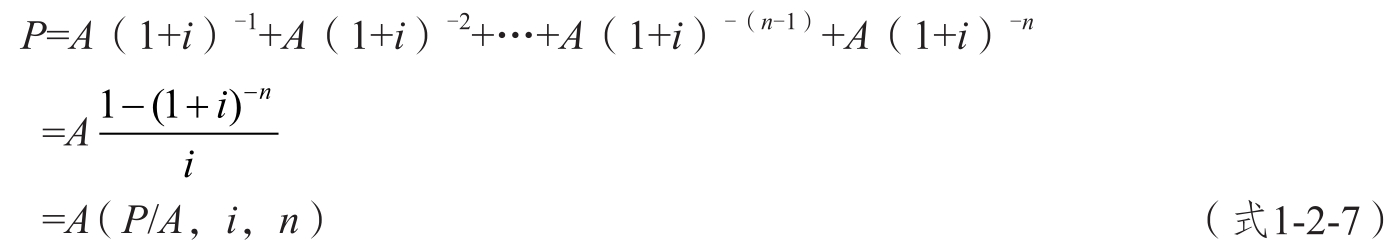
式1-2-7中，
為年金現值系數，用符號（P/A，i，n）表示，其值可查閱本書附錄中的年金現值系數表（見附表4）。
【任務1-2-8】王先生準備出國，出國期限為5年。在出國期間，他每年年末需支付1萬元的物業管理費等費用，已知銀行年利率為5%，王先生現在需要在銀行存入多少元才能保證5年中每年年末有1萬元用于支付相關費用？
【解析】P=A（P/A，i，n）=10 000×（P/A，5%，5）=10 000×4.329 5=43 295（元）。
年資本回收額是指在約定年限內等額回收初始投入資本或清償所欠債務的金額。簡單來說，就是現在投入資本或借入債務P，每期期末應等額收回或清償的金額A，即為年資本回收額。
根據P=A（P/A，i，n），推導出A=P/（P/A，i，n）或A=P（A/P，i，n）。其中，（A/P，i，n）為資本回收系數，它與年金現值系數互為倒數。
提示
普通年金終值系數和償債基金系數互為倒數，普通年金現值系數和資本回收系數互為倒數。
【任務1-2-9】若現在向銀行借10 000元，打算5年內每年年末分期還款，借款年利率為6%，則每年還款額為多少？
【解析】A=P/（P/A，i，n）=10 000/（P/A，6%，5）=10 000/4.212 4=2 373.94（元）。
技能拓展 Excel在普通年金終值及現值計算中的應用
1.使用插入函數法計算普通年金終值
本法是指在Excel環境下，通過插入財務函數FV，并根據計算機系統的提示，正確輸入已知的年金pmt、期限nper和折現率rate，從而直接求得終值FV的方法。
Excel在普通年金計算中的應用
沿用【任務1-2-6】中的有關數據，利用插入函數法確定其終值，解析如下。
【解析】從已知條件可以看出，這是要計算普通年金終值，所以可以采用函數FV進行計算，其中參數pmt為1，nper為10，rate為2%，其余參數可省略，如圖1-2-9所示。
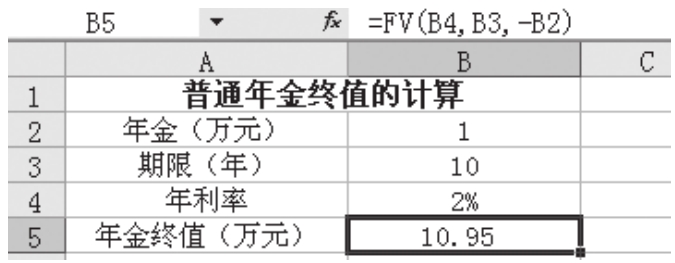
圖1-2-9 普通年金終值的計算
在圖1-2-9所示的B5單元格中輸入公式“=FV（B4，B3，-B2）”，得出李女士10年后可從銀行取出10.95萬元。
2.使用插入函數法計算普通年金現值
本法是指在Excel環境下，通過插入財務函數PV，并根據計算機系統的提示，正確輸入已知的年金pmt、期限nper和折現率rate，從而直接求得現值PV的方法。
沿用【任務1-2-8】中的有關數據，利用插入函數法確定其現值，解析如下。
【解析】從題意可知，這是要計算普通年金現值，所以可以采用函數PV進行計算，其中參數pmt為1，nper為5，rate為5%，其余參數可省略，如圖1-2-10所示。
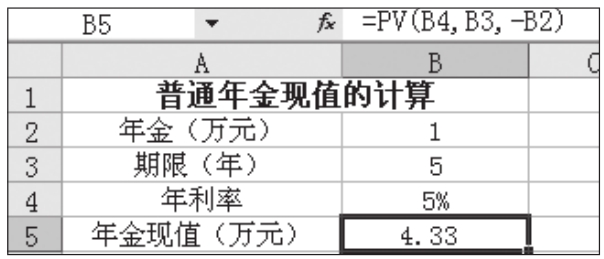
圖1-2-10 普通年金現值的計算
在圖1-2-10所示的B5單元格中輸入公式“=PV（B4，B3，-B2）”，就可以得出王先生現在應向銀行存入4.33萬元。
3.使用插入函數法計算普通年金
本法是指在Excel環境下，通過插入財務函數PMT，并根據計算機系統的提示，正確輸入已知的現值pv、終值fv、期限nper和折現率rate，從而直接求得普通年金PMT的方法。
沿用【任務1-2-7】中的有關數據，利用插入函數法確定其年金，解析如下。
【解析】從題意可知，這是要計算普通年金，所以可以采用函數PMT進行計算，其中參數fv為10 000，nper為5，rate為6%，其余參數可省略，如圖1-2-11所示。
在圖1-2-11所示的B5單元格中輸入公式“=PMT（B2，B3，，B4）”，就可以得出每年需要存入1 773.96元（圖1-2-11中“-”代表存入）。
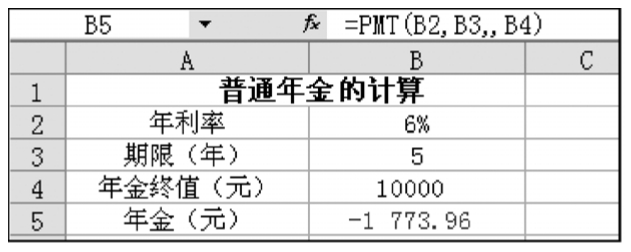
圖1-2-11 普通年金的計算
隨堂練習
（1）李某每年年末存入銀行20 000元，年利率為7%，則6年后可得到多少元？
（2）張先生擬在3年后還清200 000元的債務，年利率為3%，從現在起每年年末等額存入一筆款項，則每年需存入多少元？
（3）劉女士外出工作4年，請你代付房租，每年年末付租金20 000元。若銀行年利率為4%，她現在應該在銀行存入多少元？
（4）假設陳先生現在以10%的年利率借款50萬元，投資于某個期限為10年的項目，每年年末至少要收回多少萬元才不會虧損？
2.預付年金終值和現值的計算
預付年金是指一定時期內每期期初等額的系列收付款項，又稱先付年金或即付年金。
（1）預付年金終值的計算。預付年金的終值是各期期初等額系列收付款項的復利終值之和。通過比較圖1-2-12所示的普通年金和預付年金終值計算的時間可知，預付年金終值比普通年金終值要多一個計息期。
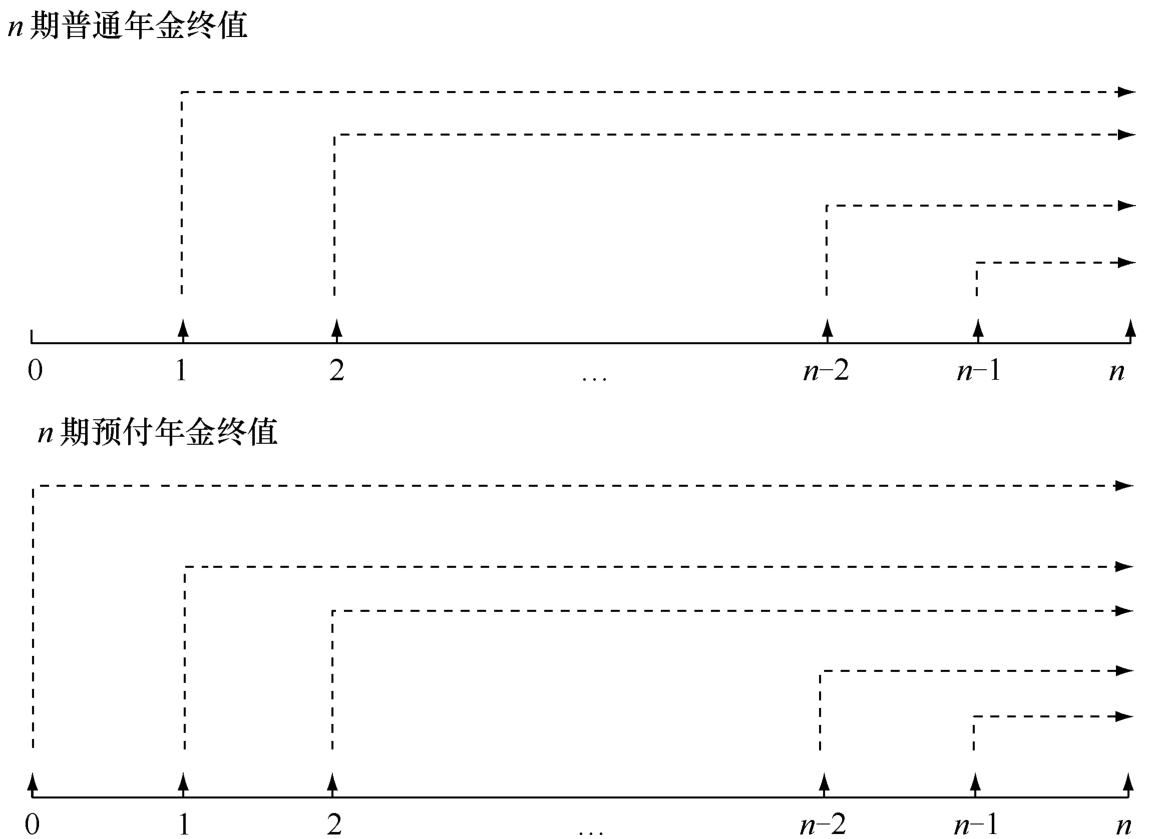
圖1-2-12 普通年金和預付年金終值計算的時間對比
預付年金終值的計算公式如下。
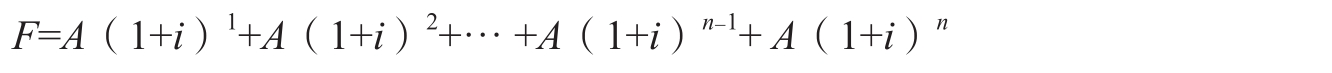
提示
預付年金終值系數通過普通年金終值系數換算，方法為“期數加1，系數減1”。
【任務1-2-10】張先生計劃每年年初向銀行存入20 000元，以便第3年年末積累一筆資金買車，若銀行存款年利率為6%，則3年后張先生共積累了多少元買車？
【解析】
方法一：F=20 000×（F/A，6%，3）（1+6%）=20 000×3.183 6×1.06=67 492.32（元）。
方法二：F=20 000×[（F/A，6%，3+1）-1]=20 000×（4.374 6-1）=67 492（元）。
（2）預付年金現值的計算。預付年金的現值是各期期初等額系列收付款項的復利現值之和。通過比較圖1-2-13所示的普通年金和預付年金現值計算的時間可知，預付年金現值比普通年金現值少折現一期。
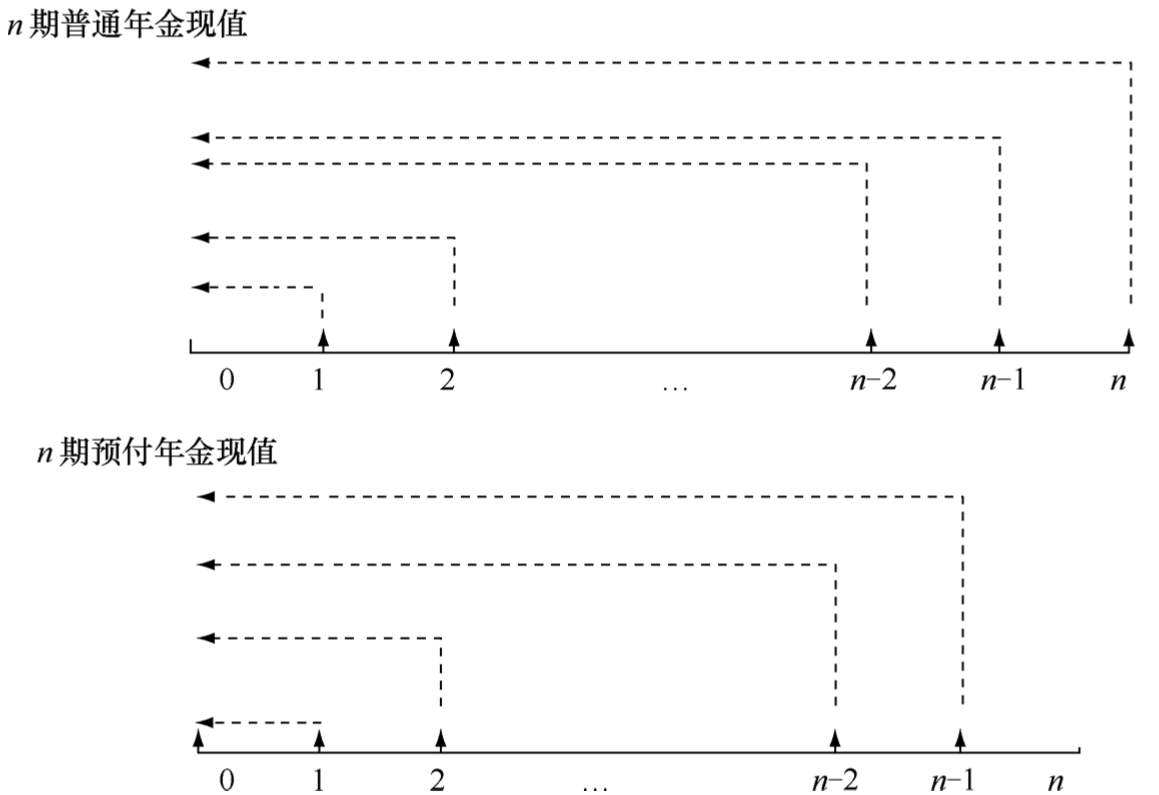
圖1-2-13 普通年金和預付年金現值計算的時間對比
預付年金現值的計算公式如下。
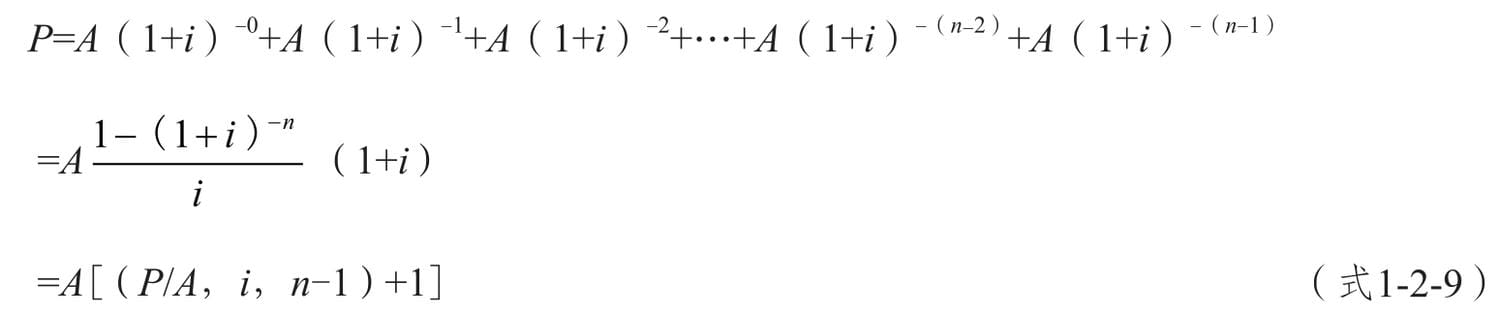
提示
預付年金現值系數通過普通年金現值系數換算，方法為“期數減1，系數加1”。
【任務1-2-11】王先生擬購一套住房，開發商提出兩種方案，一是現在一次性付800萬元，二是從現在起每年年初付200萬元，連續支付5年。若目前的銀行貸款年利率為7%，則王先生應選擇哪種付款方案？
【解析】方案一中現值P=800（萬元）。
方案二中現值P=200×（P/A，7%，5）（1+7%）=200×4.100 2×1.07=877.44（萬元）。
由于方案一現值小于方案二的現值，所以選擇方案一。
技能拓展 Excel在預付年金終值及現值計算中的應用
預付年金終值及現值的計算方法與普通年金的相似，主要區別在于計算預付年金終值及現值時要將參數type設為1。
Excel在預付年金終值及現值計算中的應用
隨堂練習
（1）為了給女兒上大學準備資金，劉女士計劃未來6年每年年初存入銀行10 000元，若銀行年利率為5%，則劉女士在第6年年末能一次性取出多少本利和？
（2）甲公司在2023年租入一臺設備，租期為5年，若每年年初支付租金30 000元，年利率為6%，則5年中租金的總現值為多少？
3.遞延年金終值和現值的計算
遞延年金，又叫延期年金，是指在最初若干期沒有收付款項的情況下，隨后若干期發生的等額系列收付款項。遞延年金是一種特殊的普通年金。m期以后的n期遞延年金如圖1-2-14所示。
從圖1-2-14中可以看出，前m期（m表示遞延期）沒有發生現金收付，第一次收付發生在m+1期期末，連續收付n期（n表示收付期）。
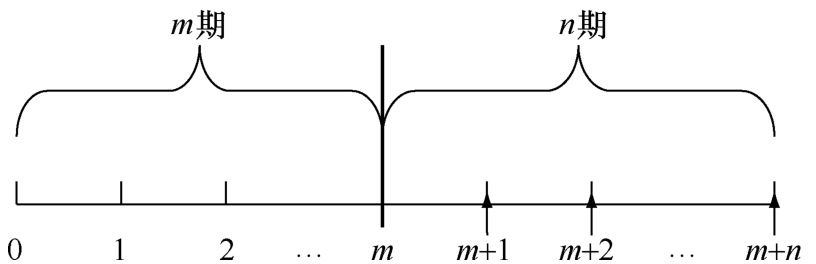
圖1-2-14 遞延年金
（1）遞延年金終值的計算。遞延年金終值只與收付期有關，與遞延期無關。其計算方法與普通年金終值的計算方法相似，即
提示
n表示A的個數，與遞延期無關。
（2）遞延年金現值的計算。遞延年金現值的計算有以下3種方法。
①補缺法。假設遞延期中也發生等額系列收付款項，先計算出m+n期的普通年金現值，然后扣除實際并未收付的m期年金現值，即可得到遞延年金現值。公式如下。
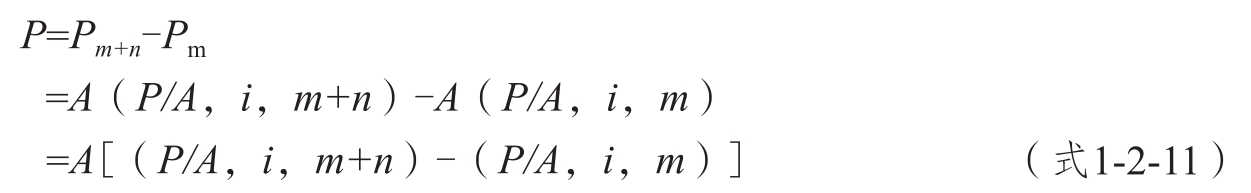
②分段法。將遞延年金看成n期普通年金，先求出m期期末的現值，然后再將此現值折算到第一期期初，即可得到n期遞延年金現值。公式如下。
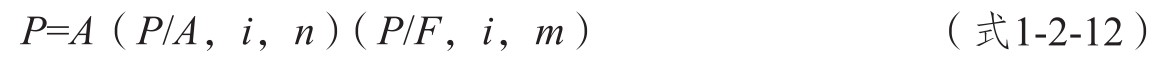
③折終折現法。先計算遞延年金在m+n期期末的終值，然后將此終值折算到第一期期初求現值，即可得到遞延年金現值。公式如下。
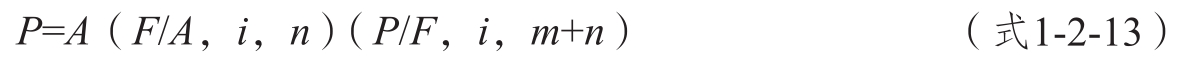
提示
在計算遞延年金現值之前，一定要準確判斷遞延期的數值。如何確定遞延期呢？
（1）知道遞延年金的第一次收付發生在第幾期期末（假設為第X期期末）。
（2）根據（X-1）的數值即可確定遞延期。
【任務1-2-12】某企業進行項目投資，該項目于2019年年初動工，施工期為3年，于2022年年初建成投產，從投產之日起每年年末得到收益4萬元。按年利率6%計算，則10年后的收益于2019年年初的現值是多少？
【解析】方法一：P=4×[（P/A，6%，13）-（P/A，6%，3）]=4×（8.852 7-2.673）=24.72（萬元）。
方法二：P=4×（P/A，6%，10）（P/F，6%，3）=4×7.360 1×0.839 6=24.72（萬元）。
方法三：P=4×（F/A，6%，10）（P/F，6%，13）=4×13.180 8×0.468 8=24.72（萬元）。
技能拓展 Excel在遞延年金終值及現值計算中的應用
1.使用插入函數法計算遞延年金終值
遞延年金終值只與收付期n有關，與遞延期m無關，所以m+n期期末的遞延年金終值可以按照n期的普通年金終值的公式計算。
2.使用插入函數法計算遞延年金現值
沿用【任務1-2-12】中的有關數據，利用插入函數法確定其現值，解析如下。
【解析】從題意可知，這是要計算遞延年金現值，其中遞延期為3年，年金為4萬元，年利率為6%，有10年的普通年金，可以按以下3種方法計算。
Excel在遞延年金終值及現值計算中的應用
（1）補缺法。在圖1-2-15所示的B6單元格中輸入公式“=PV（B5，B3+B4，B2）”，計算出第13年的普通年金現值是35.41萬元；在B7單元格中輸入公式“=PV（B5，B4，B2）”，計算出遞延期3年的年金現值是10.69萬元；最后在B8單元格中輸入公式“=B6-B7”，即可計算出它的現值是24.72萬元。
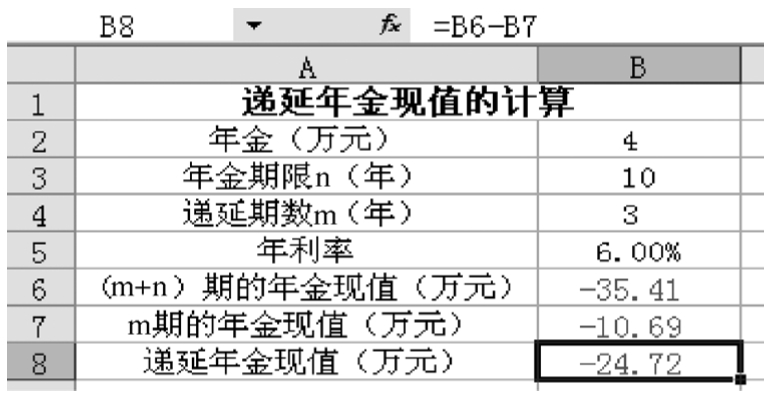
圖1-2-15 遞延年金現值的計算——補缺法
（2）分段法。在圖1-2-16所示的B6單元格中輸入公式“=PV（B5，B3，B2，，0）”，計算出第3年年末的普通年金現值是29.44萬元，然后以此結果作為終值，在B7單元格中輸入公式“=PV（B5，B4，，-B6）”，計算出它的現值是24.72萬元。
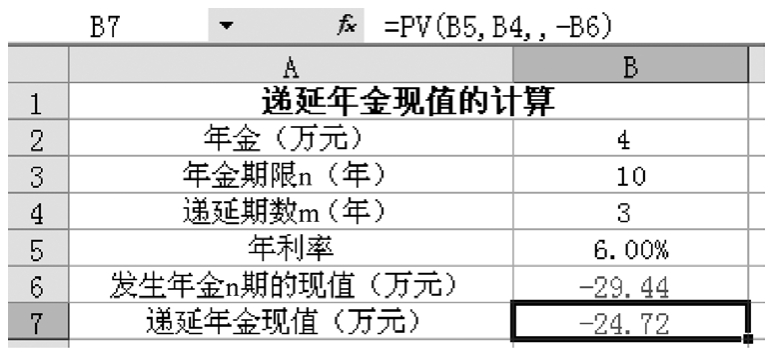
圖1-2-16 遞延年金現值的計算——分段法
（3）折終折現法。在圖1-2-17所示的B6單元格中輸入公式“=FV（B5，B3，B2）”，計算出第13年年末的遞延年金終值為52.72萬元，然后以此結果作為終值，在B7單元格中輸入公式“=PV（B5，B3+B4，，-B6）”，計算出它的現值是24.72萬元。
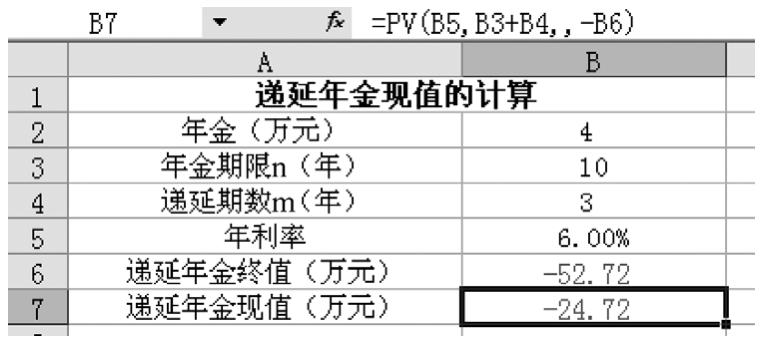
圖1-2-17 遞延年金現值的計算——折終折現法
隨堂練習
（1）有一項年金，從第3年年末起，每年年末取出20 000元，直至第6年年末全部取完，年利率為8%，最初一次存入銀行的款項為多少？
（2）有一項年金，前3年年初無流入，后5年每年年初流入50 000元，年利率為10%，該項年金的現值為多少？
4.永續年金現值的計算
永續年金是指無限期等額收付的年金，可視為普通年金的特殊形式，即期限趨于無窮的普通年金，如圖1-2-18所示。日常生活中，存本取息、優先股、獎學金都可視為永續年金的例子。
圖1-2-18 永續年金
由于永續年金持續期趨于無窮大，沒有終止的時間，因此沒有終值。永續年金現值的計算公式可以通過普通年金現值的計算公式推導得出。
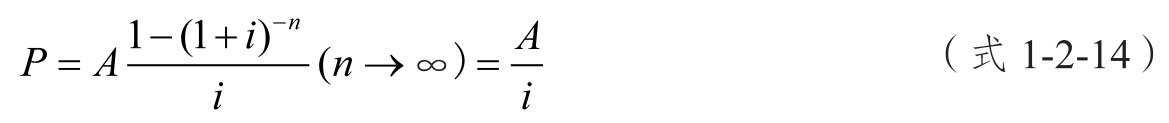
提示
除了永續年金沒有終值，其他種類的年金都有終值。
【任務1-2-13】某學校設立永久性獎學金，每年計劃發放50 000元，若年利率為8%，則該項獎學金的本金應為多少？
【解析】P=A/i=50 000/8%=625 000（元）。
隨堂練習
某企業想給學校創立一個永久性的愛心基金，希望每年能從該基金中拿出10萬元用于經濟困難學生的生活補助。若年利率為4%，則企業要向學校捐贈多少元才能創建該愛心基金呢？
知識鏈接 混合收付款項現值、終值的計算及利率的計算
1.混合收付款項現值和終值的計算
混合收付款項是指各期不相等的收付款項。對于混合收付款項終值（現值）的計算，可先計算出每次收付款項的復利終值（現值），然后加總得到最終結果。
【任務1-2-14】劉先生準備第1年年末存入銀行1萬元，第2年年末存入銀行3萬元，第3～5年每年年末存入銀行4萬元，存款年利率為10%，則這5年存款的現值合計是多少？
【解析】P=1×（P/F，10%，1）+3×（P/F，10%，2）+4×[（P/F，10%，3）+（P/F，10%，4）+（P/F，10%，5）]
=1×0.909 1+3×0.826 4+4×（0.751 3+0.683 0+0.620 9）
=11.61（萬元）。
2.利率的計算
計算利率時，首先要計算出有關的資金時間價值系數，然后查找相應的系數表（如復利終值系數表、復利現值系數表、年金終值系數表、年金現值系數表）。如果在系數表中能找到這個系數值，則對應的利率即為所求的利率；如果不能，則在系數表中找出最接近該系數值的一大一小兩個系數及其對應的利率，運用內插法求出利率。
內插法一般是指數學上的直線內插法，其原理是根據比例關系建立一個方程，然后解方程計算得出所求的數據。內插法在財務管理中的應用很廣泛，如在復利計息方式下，利率與現值（終值）系數之間存在一定的數量關系。已知現值（或終值）系數，則可以通過內插法計算對應的利率。
式1-2-15中，所求利率為i，與i對應的現值（終值）系數為B，B1、B2為現值（終值）系數表中與B相鄰的系數，i1、i2為B1、B2對應的利率。
利率與系數值的關系如圖1-2-19所示。
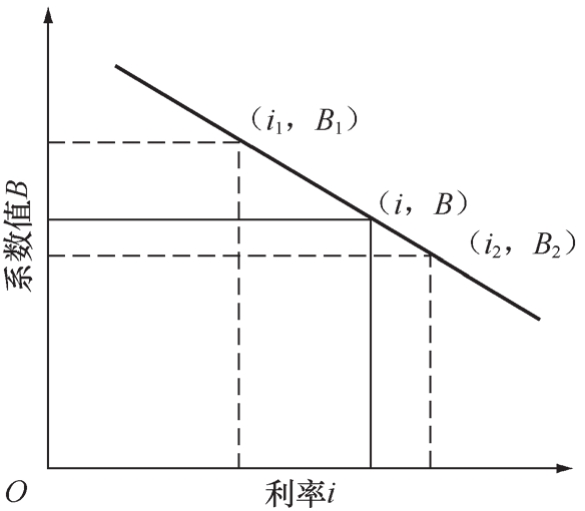
圖1-2-19 利率與系數值的關系
【任務1-2-15】某公司因資金周轉需要在第1年年初借款30 000元，雙方約定每年年末還款5 000元，連續8年還清，則此項借款年利率為多少？
【解析】根據題意，已知P=30 000，A=5 000，n=8，求i。
由P=A（P/A，i，n）可得，
30 000=5 000×（P/A，i，8），則（P/A，i，8）=6。
查年金現值系數表，當n=8時，
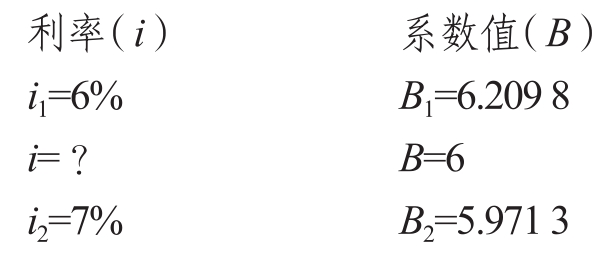
根據內插法可得，
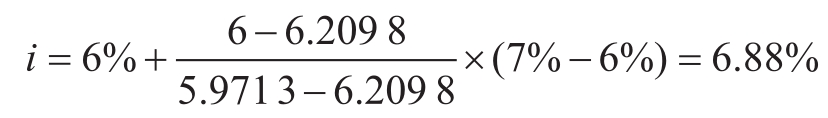
3.計息期的計算
在已知現值、終值、年金、利率等要素的情況下，計息期的計算方法和利率的計算方法相同，也可使用內插法計算，本書不做詳細介紹，感興趣的讀者可查閱資料了解。
技能拓展 Excel在利率及計息期計算中的應用
1.使用插入函數法計算利率
本法是指在Excel環境下，通過插入財務函數RATE，并根據計算機系統的提示，正確輸入已知的現值pv、終值fv、期限nper、年金pmt和估計利率guess，從而直接求得利率RATE的方法。
Excel在利率及計息期計算中的應用
注：參數估計利率guess如果與實際利率相差較大，則會出現錯誤，需要重新估計；如果省略不寫，則假定該值為10%。通常情況下該參數可省略。
沿用【任務1-2-15】中的有關數據，利用插入函數法確定其利率，解析如下。
【解析】從題意可知，這是要計算普通年金利率，可以采用函數RATE進行計算，其中參數pv為30 000，pmt為5 000，nper為8，其余參數省略，如圖1-2-20所示。
在圖1-2-20所示的B5單元格中輸入公式“=RATE（B3，-B2，B4）”，就可以得出此項借款年利率為6.88%。
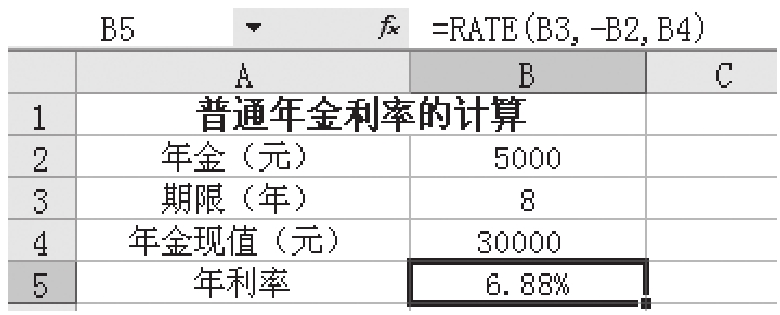
圖1-2-20 普通年金利率的計算
2.使用插入函數法計算計息期
本法是指在Excel環境下，通過插入財務函數NPER，并根據計算機系統的提示，正確輸入已知的現值pv、終值fv、年金pmt和利率rate，從而直接求得計息期NPER的方法。計息期函數NPER的使用方法與利率函數RATE的使用方法相似，此處不再詳細介紹。
大數據應用 基于文本挖掘技術分析股民情感指數與股價變化的影響關系
作為金融市場的重要組成部分，股票市場對促進國民經濟發展和推動世界經濟一體化進程具有重要的作用。而對現代股票市場而言，網絡已成為交易的重要平臺之一，實時股評中包含豐富的金融信息，體現了投資者的情緒變化。因此，對股市的研究可以考慮從股評入手進行挖掘分析。
利用文本挖掘方法對在東方財富網股吧抓取的上證指數股評文本進行分析，并據此利用基于情感詞典的方法研究評論的情感傾向，可以分析股評者的心理狀態及非理性行為，得出股票價格變化與投資者情緒變化之間的影響關系，為投資決策的制定提供參考。
文本挖掘之情感分析（上）
文本挖掘之情感分析（中）
文本挖掘之情感分析（下）
股民情感與股票價格之間的關系——Python代碼實現
任務小結
資金時間價值是指一定量的資金在不同時點上的價值量的差額。在對這一概念理解的基礎上，不僅需要記住一次性收付款項終值與現值公式、4種年金終值和現值公式，而且還要掌握它們的計算方法。
閱讀案例
股票估價與投資決策分析
鞏固與提升
一、單項選擇題
1.甲某擬存入一筆資金以備3年后使用。假定銀行3年期存款年利率為5%，甲某3年后需用的資金總額為34 500元，則在單利計息情況下，目前需存入的資金為（ ）元。
A.30 000
B.29 803.04
C.32 857.14
D.31 500
2.如果某人現有退休金100 000元，準備存入銀行。在銀行年利率為4%的情況下，其10年后可以從銀行取得（ ）元。
A.140 000
B.148 020
C.120 000
D.150 000
3.一定時期內每期期初等額收付的系列款項是（ ）。
A.預付年金
B.永續年金
C.遞延年金
D.普通年金
4.某企業擬建立一項基金，每年年初投入100 000元，若年利率為10%，5年后該項基金本利和為（ ）元。
A.671 561
B.564 100
C.871 600
D.610 500
5.在普通年金終值系數的基礎上，期數加l、系數減1所得的結果，在數值上等于（ ）。
A.普通年金現值系數
B.預付年金現值系數
C.普通年金終值系數
D.預付年金終值系數
6.已知（P/A，10%，4）=3.169 9，（P/A，10%，5）=3.790 8，（P/A，10%，6）=4.355 3，則5年期、折現率為10%的預付年金現值系數是（ ）。
A.4.169 9
B.4.790 8
C.5.355 3
D.6.206 4
7.已知（P/A，12%，9）=5.328 2，（P/A，14%，9）=4.946 4，某公司向銀行借入20 000元，借款期為9年，每年年末的還本付息額為4 000元，則借款年利率為（ ）。
A.13.06%
B.13.72%
C.15.36%
D.16.5%
8.已知（F/A，10%，9）=13.579 5，（F/A，10%，11）=18.531 2，則10年期、年利率為10%的預付年金終值系數為（ ）。
A.17.531 2
B.15.937 2
C.14.579 5
D.12.579 5
9.某公司擬于5年后一次性還清所欠債務100 000元，假定銀行利率為10%，5年期，年利率為10%的普通年金終值系數為6.105 1；5年期，年利率為10%的普通年金現值系數為3.790 8，則應從現在起每年年末等額存入銀行的償債基金為（ ）元。
A.16 379.75
B.26 379.66
C.379 080
D.610 510
10.在下列各項資金時間價值系數中，與資本回收系數互為倒數關系的是（ ）。
A.（P/F,i,n）
B.（P/A,i,n）
C.（F/P,i,n）
D.（F/A,i,n）
二、多項選擇題
1.下列屬于年金特點的有（ ）。
A.每次發生的金額相等
B.每次發生的時間間隔相同
C.每次發生的金額必須相等，但每次發生的時間間隔可以不同
D.每次發生的金額可以不相等，但每次發生的時間間隔必須相同
2.永續年金的特點有（ ）。
A.沒有終值
B.期限趨于無窮大
C.只有現值
D.每期等額收付
3.某公司向銀行借入一筆款項，年利率為10%，分6次還清，第5～10年每年年末償還本息5 000元。下列計算該筆借款現值的算式中，正確的有（ ）。
A.5 000×（P/A,10%,6）×（P/F,10%,3）
B.5 000×（P/A,10%,6）×（P/F,10%,4）
C.5 000×[（P/A,10%,9）-（P/A,10%,3）]
D.5 000×[（P/A,10%,10）-（P/A,10%,4）]
4.下列各項中可以直接或間接利用普通年金終值系數計算出確切結果的有（ ）。
A.償債基金
B.預付年金終值
C.永續年金現值
D.永續年金終值
5.下列關于資金時間價值系數關系的表述，正確的有（ ）。
A.普通年金現值系數×資本回收系數=1
B.普通年金終值系數×償債基金系數=1
C.普通年金現值系數×（1+折現率）=預付年金現值系數
D.普通年金終值系數×（1+折現率）=預付年金終值系數
三、判斷題
1.終值是本金和利息之和。（ ）
2.即使只有一筆款項的發生額不相等，該系列款項也不能被稱為年金。（ ）
3.普通年金現值系數加1等于同期、同利率的預付年金現值系數。（ ）
4.國庫券是一種幾乎沒有風險的有價證券，那么其利率可以代表資金時間價值。（ ）
5.在終值和計息期一定的情況下，折現率越低，復利現值越大。（ ）
四、課后任務
要求學生在網上查找某保險公司資料，進一步掌握一次性收付款項的終值與現值、年金的終值與現值等計算資金時間價值的方法。