1.4　既約分數(★)

題目信息

2020 年省賽-填空題

● C/C++ A組第2題；C/C++ B組第2題

● Java A組第2題

【問題描述】

如果一個分數的分子和分母的最大公約數是 ，這個分數稱為既約分數。

例如 ， 都是既約分數。

請問，有多少個既約分數，分子和分母都是?1?到?2020?之間的整數（包括?1?和?2020?）？

【答案提交】

這是一道結果填空題，你只需要算出結果后提交即可。本題的結果作為一個整數，在提交答案時只填寫這個整數，填寫多余的內容將無法得分。

題目分析

核心考點

● gcd（最大公約數）

用一句話概括題意，即統計分子、分母的范圍均為 1 2020 且分子、分母的最大公約數（gcd）為 1 的分數的個數。

解題的思路較為簡單，只需從 1 2020 枚舉分子，再從 1 2020 枚舉分母，然后判斷分子、分母的最大公約數是否為 1（若為 1 則答案個數+1）即可。不過在此之前，我們需要知道如何求解兩個數的最大公約數。

求最大公約數的方法很多，如果想圖個方便，可以直接調用 C++的 algorithm 庫中的 ＿gcd() 函數來求解。如果不知道這個函數也沒有關系，因為想求解兩個數的最大公約數并不難。我們可以采用常用的輾轉相除法（國際上也稱"歐幾里得算法"），它的代碼如下。

參考代碼1-4-1　【復雜度為 】

 1   int gcd(int a , int b){
 2       if(b == 0) return a;
 3       return gcd(b, a % b);
4   }

知道了如何求解兩個數的最大公約數后，就可以枚舉統計答案了。

參考代碼1-4-2　【復雜度為 】

 1   #include<bits/stdc++.h>
 2   using namespace std;
 3   signed main()
 4   {
 5       int ans = 0;
 6       for(int i = 1 ; i <= 2020 ; i ++){
 7           for(int j = 1 ; j <= 2020 ; j ++){
 8               if(＿gcd(i , j) == 1) ans ++ ;
 9           }
10       }
11       cout << ans << '\n';
12       return 0;
13   }

最終答案為2481215。

拓展提高

我們來考慮一下如何優化程序的時間復雜度。

若兩個數 （ ）的最大公約數為 1，則 是一個既約分數， 也是一個既約分數。所以我們可以從 枚舉 ，從 枚舉 ，這樣得到的 就滿足 。接著判斷 的最大公約數是否為 1（若為 1，則 是既約分數）。

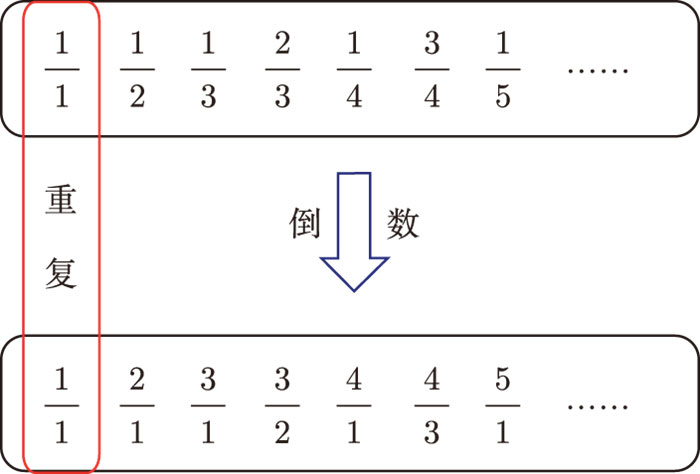
若用 cnt 來統計有多少對 滿足 且 的最大公約數為 1，則答案為 （乘2是因為 的倒數 也是既約分數，減 1 是因為 的倒數還是 ，重復計算了一次，要減掉，見下圖）。

這樣就可以細微地優化程序計算的次數了。

不過程序的復雜度仍為 。有沒有什么辦法能降低復雜度呢?答案自然是有。

核心考點

● 唯一分解定理

● 歐拉函數

● 歐拉篩

對于最大公約數為 1 的兩個整數，我們稱它們的關系為互質。在數論中， 中與 互質的數的個數被稱為歐拉函數（記作 ）。

由歐拉函數的定義可知滿足 ，且 最大公約數為 的 的個數就為 。

我們要求的是 內滿足 且 最大公約數為 1 的 的個數，即 內所有數的歐拉函數的和，即 。

歐拉函數的通項公式：

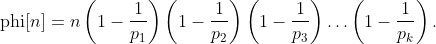
其中 為 的所有不重復質因子。

要想得到 的所有不重復質因子，我們可以采用數論利器——唯一分解定理。

提示

唯一分解定理就是對于一個大于 的整數 ，要么其本身是個質數，要么能被分解為有限個質數的乘積。

若用數學公式表示，則 ， 表示質數（即 的質因子）， 表示 的個數。

例如， 就可以表示為 ，它的質因子有 、 。其中質因子 的個數為 ，質因子 的個數為 。

綜上，我們可以寫出如下代碼，完成對 的不重復質因子的求解。

參考代碼1-4-3

 1   int p[N];               // p[] 記錄因子，p[1]是最小因子
 2   int getPrime(int n){
 3       int k = 0; // k 記錄 n 的質因子的個數
 4       for(int i = 2 ; i * i <= n ; i ++){
 5           if(n % i == 0) {
 6               p[++ k] = i;
 7               while(n % i == 0) n /= i;  // 把 n 重復的質因子去掉
 8           }
 9       }
10       if(n > 1) p[++ k] = n;   // n 沒有被除盡，是素數
11       return n;
12   }

再根據歐拉函數的通項公式 寫出代碼。

參考代碼1-4-4

 1   int getPhi(int n){
 2       int phi = n , k = getPrime(n);
 3       for(int i = 1 ; i <= k ; i ++){ // 枚舉所有質因子：p1,p2,...,pk
 4           phi = phi -  phi / p[i]; // (phi - phi / p[i])等價于 phi(1 - 1 / p[i])
 5       }
 6       return phi;
7   }

因為在本題中質因子的作用只是為了計算歐拉函數，所以可以不用開辟數組記錄質因子，而是每得到一個質因子就將其放入歐拉函數的通項公式中計算，這樣兩份代碼就能合并在一起，具體代碼可見參考代碼1-4-5的第 行。

參考代碼1-4-5　【時間復雜度為 】

 1   #include<bits/stdc++.h>
 2   using namespace std;
 3   int solve(int n){
 4       int phi = n;
 5       for(int i = 2 ; i * i <= n ; i ++){
 6           if(n % i == 0) { // i 是 n 的質因子
 7               phi = phi - phi / i; // 將其丟入歐拉函數的通項公式中計算
 8               while(n % i == 0) n /= i;  // 把 n 重復的質因子去掉
 9           }
10       }
11       if(n > 1) phi = phi - phi / n;   // n 沒有被除盡，是素數，將其丟入歐拉函數的通項公式中計算
12       return phi;
13   }
14   signed main()
15   {
16       int ans = 0;
17       for(int i = 1 ; i <= 2020 ; i ++) ans += solve(i);
18       cout << ans * 2 - 1 << '\n';
19       return 0;
20   }

當然，求一個數的歐拉函數還有更好的求法，比如用Pollard_Rho 尋找因子、用Miller_Rabin 測試質數，以將復雜度優化到 。不過這種做法碼量極大，所涉及的知識點難度也高，藍橋杯賽場上幾乎是不可能用上的。

此外，我們還可以使用歐拉篩，它的作用是以 的時間復雜度求出 中每個數的歐拉函數。這樣，程序的復雜度就可以被進一步優化。

參考代碼1-4-6　【時間復雜度為 】

 1   #include<bits/stdc++.h>
 2   using namespace std;
 3   int n , phi[2021] , prime[2021];
 4   signed main(){
 5       // 歐拉篩
 6       phi[1] = 1;
 7       for(int i = 2 ; i <= 2020 ; i ++){
 8           if(!prime[i]) prime[++ n] = i, phi[i] = i - 1;
 9           for(int j = 1 ; j <= n && i * prime[j] <= 2020 ; j ++){
10               prime[prime[j] * i] = 1;
11               if(i % prime[j] == 0){
12                   phi[i * prime[j]] = phi[i] * prime[j];
13                   break ;
14               }
15               phi[i * prime[j]] = phi[i] * (prime[j] - 1);
16           }
17       }
18       int cnt = 0;
19       for(int i = 1 ; i <= 2020 ; i ++) cnt += phi[i];
20       cout << 2 * cnt - 1 << '\n';
21       return 0;
22   }