4.1.2　線性模型的圖形表示

大家肯定還記得，我們在初中數學（也可能是小學數學）中學過，兩個點可以確定一條直線。假設有兩個點，它們的坐標是（1，3）和（4，5），那么我們可以畫一條直線來穿過這兩個點，并且計算出這條直線的方程。下面我們在Jupyter Notebook中輸入代碼如下：

運行代碼，將會得到如圖4-2所示的結果。

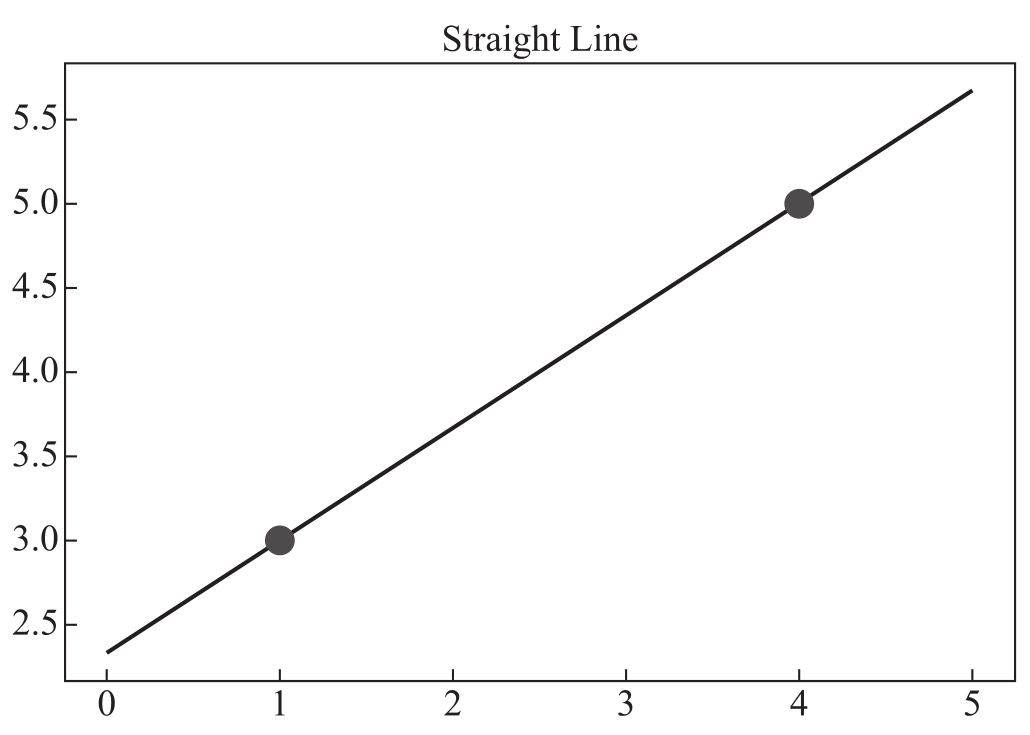
圖4-2　穿過點（1，3）和（4，5）的直線

【結果分析】圖4-2表示的就是穿過上述兩個數據點的直線，現在我們可以確定這條直線的方程。

在Jupyter Notebook中輸入代碼如下：

print('\n\n\n直線方程為：')
print('==========\n')
#打印直線方程
print('y = {:.3f}'.format(lr.coef_[0]),'x','+ {:.3f}'.format(lr.intercept_))
print('\n==========')
print('\n\n\n')

運行代碼，將會得到如圖4-3所示的結果。

圖4-3　程序計算出的直線方程

【結果分析】通過程序的計算，我們很容易就可以得到這條直線的方程為

y = 0.667 x + 2.333

這是數據中只有2個點的情況，那如果是3個點會是怎樣的情況呢？我們來實驗一下，假設現在有第3個點，坐標是（3，3），我們把這個點添加進去，看會得到怎樣的結果。輸入代碼如下：

運行代碼，會得到如圖4-4所示的結果。

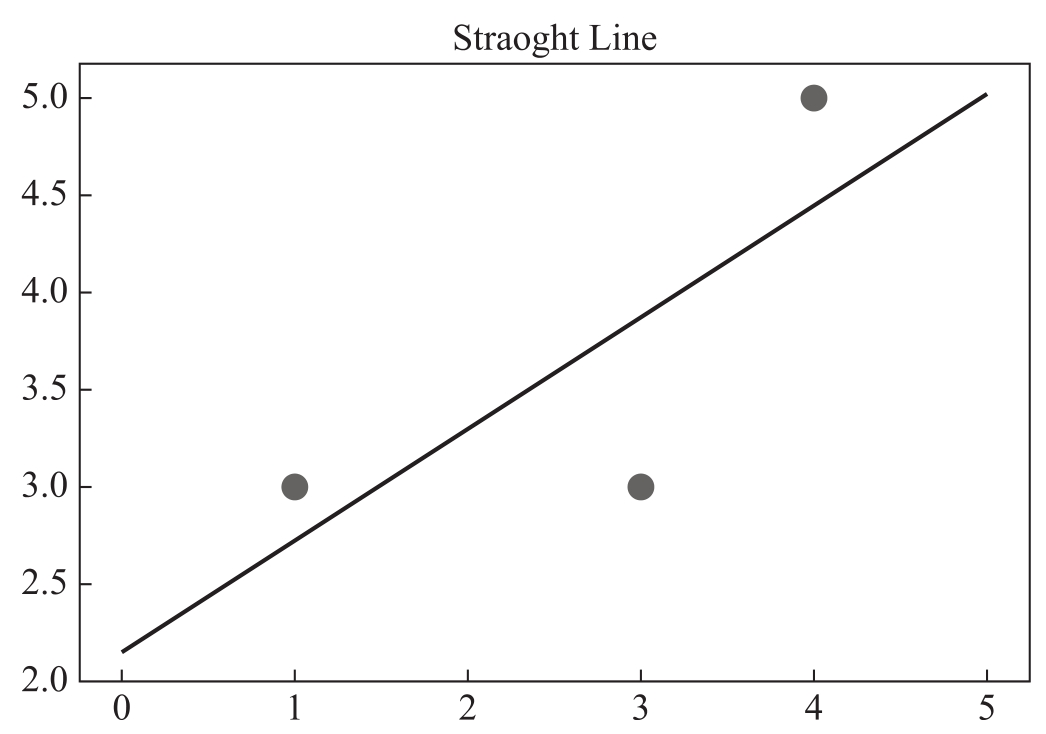
圖4-4　對3個點進行擬合的線性模型

【結果分析】從圖4-4中我們可以看到，這次直線沒有穿過任何一個點，而是位于一個和3個點的距離相加最小的位置。

下面我們可以在計算出這條直線的方程，輸入代碼如下：

print('\n\n\n新的直線方程為：')
print('==========\n')
#打印直線方程
print('y = {:.3f}'.format(lr.coef_[0]),'x','+ {:.3f}'.format(lr.intercept_))
print('\n==========')
print('\n\n\n')

圖4-5　對3個點進行擬合的線性模型方程

運行代碼，將會得到結果如圖4-5所示。

【結果分析】從圖4-5中我們可以看到，新的直線方程和只有2個數據點的直線方程已經發生了變化。線性模型讓自己距離每個數據點的加和為最小值。這也就是線性回歸模型的原理。

當然，在實際應用中，數據量要遠遠大于2個或是3個，下面我們就用數量更多的數據來進行實驗。

現在我們以scikit-klearn生成的make_regression數據集為例，用Python語句繪制一條線性模型的預測線，更加清晰地反映出線性模型的原理。在jupyter notebook中輸入代碼如下：

按下shift+回車鍵后，會得到結果如圖4-6所示的結果。

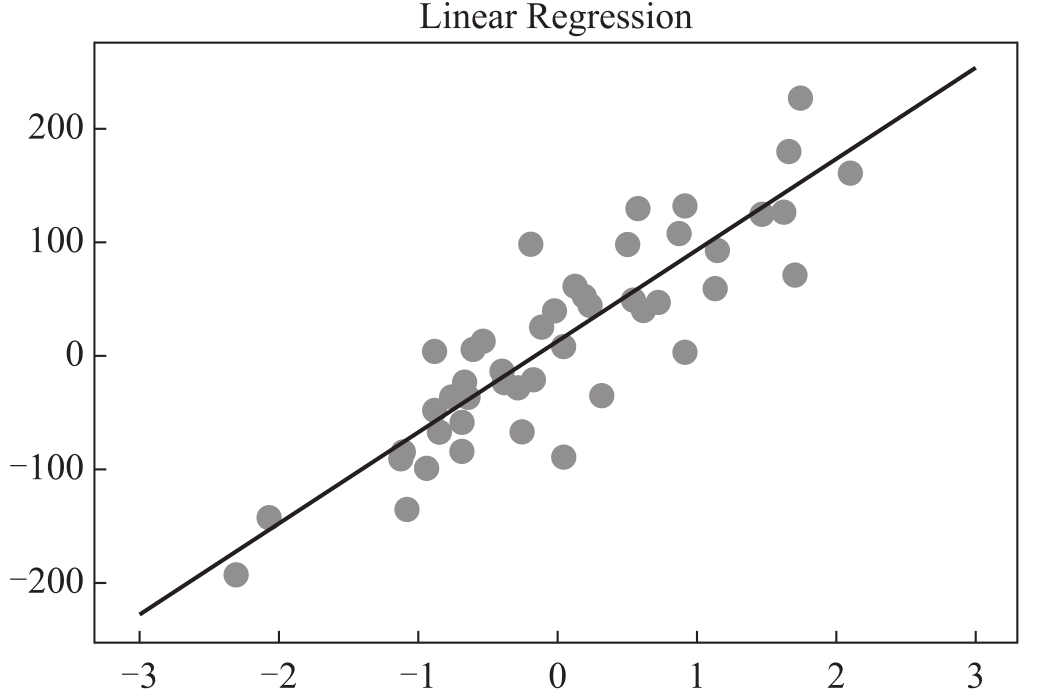
圖4-6　線性回歸模型的預測線

【結果分析】從圖4-1中我們可以看出，黑色直線是線性回歸模型在make_regression數據集中生成的預測線。接下來我們來看一下這條直線所對應的斜率和截距。

輸入代碼如下：

print('\n\n\n代碼運行結果：')
print('==========\n')
#打印直線的系數和截距
print('直線的系數是：{:.2f}'.format(reg.coef_[0]))
print('直線的截距是：{:.2f}'.format(reg.intercept_))
print('\n==========')
print('\n\n\n')

運行代碼，會得到結果如圖4-7所示。

圖4-7　直線的系數和截距

【結果分析】從圖4-7中我們可以看到，在我們手工生成的數據集中，線性模型的方程為

y = 79.52 x +10.92

而這條直線距離50個數據點的距離之和，是最小的。這便是一般線性模型的原理。

注意　細心的讀者可能注意到coef_和intercept_這兩個屬性非常奇怪，它們都是以下劃線_結尾。這是sciki-learn的一個特點，它總是用下劃線作為來自訓練數據集的屬性的結尾，以便將它們與由用戶設置的參數區分開。