1.2.3 動作價值函數和狀態-動作價值函數

有了回報的定義，結合前面提到的條件概率p_π（r_t，s_t+1|a_t，s_t），就可以進一步定義價值函數（Value Function）和動作-價值函數（Action-Value Function，又稱Q函數），如式（1.4）和式（1.5）所示。

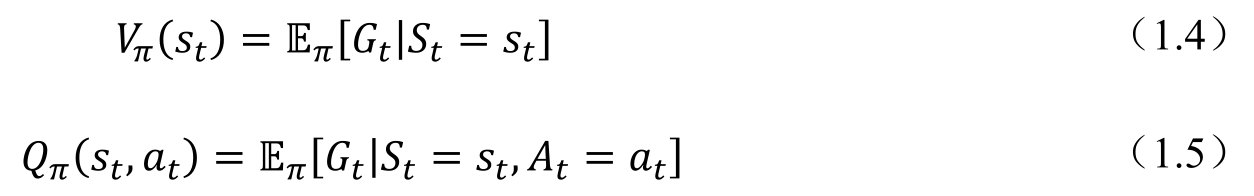
可以看到，式（1.4）和式（1.5）中的函數都有一個下標π，這里代表智能體的價值函數和動作-價值函數都是在給定的策略條件下計算得到的。這里的策略按照算法的不同，可以是后面介紹的策略神經網絡生成的一組策略，也可以是隨機策略或者貪心策略。另外，式（1.4）和式（1.5）中的兩個函數都是對策略的期望，意味著在實際過程中，需要一段比較長的時間，在固定策略的情況下，通過智能體的不斷行動，對不同狀態或狀態-動作進行采樣，對采樣的結果計算對應的回報值，取對應的期望，進而求得最終的價值函數或者動作價值函數的值。

可以很容易地看到，式（1.4）是式（1.5）對于不同動作的期望，如式（1.6）所示，其中，A為當前狀態下所有可能動作的集合，而π（a_t|s_t）是給定當前狀態s_t，智能體做出動作a_t的概率，這個條件概率可以認為描述了策略的分布。于是我們可以看到，其實V_π（s_t）可以認為是Q_π（s_t，a_t）在當前策略下的平均表現。在很多情況下，想要知道某個動作預期能夠得到的回報是好于平均還是差于平均，這時就需要引入一個函數A_π（s_t，a_t），我們稱之為優勢函數（Advantage Function），用這個函數來衡量當前動作的好壞，如式（1.7）所示。這個公式的原理同樣很簡單，就是用當前的動作-價值函數減去動作函數，如果函數大于零，說明這個動作的表現好于平均，反之，則差于平均。

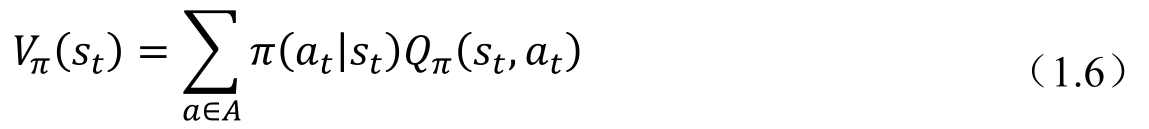
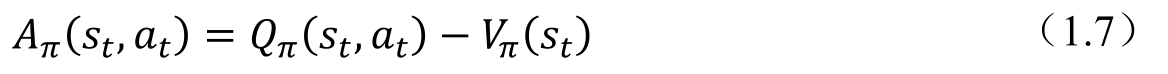
價值函數和動作-價值函數對于深度強化學習非常重要。在基于策略的深度強化學習算法中，為了了解一個策略的好壞，算法需要對當前策略的價值函數或者動作-價值函數進行估計，當一個策略能夠提升這兩個函數的時候，該策略才是好的策略，要盡可能往該方向優化；而算法應該盡可能避免價值函數的降低。在價值的深度強化學習算法中，由于一般情況下取的策略是平凡策略（如貪心策略，總是往價值高的狀態前進），算法也需要知道具體某種動作和某種狀態的價值，以確定采取的動作。為了估計這兩個函數，人們引入了貝爾曼方程（Bellman Equation），通過迭代的方法來對這兩個函數進行估計。這里先簡單列出公式，以便讀者參考（讀者也可以在第2章中找到詳細的推導過程）。為了方便讀者理解，這里做一個簡單的解釋。前面已經在動態規劃的部分介紹過，價值函數的求解是一個迭代的過程，而貝爾曼方程給出的就是如何進行迭代計算的公式。式（1.8）和式（1.9）比較類似，假如在某一次迭代中已經有了一個V_π（s_t+1）和Q_π（s_t+1，a_t+1），為了能夠得到下一次迭代的值，需要有當前迭代步驟時t時間的獎勵r_t，結合前面所說的已經有的V_π（s_t+1）和Q_π（s_t+1，a_t+1），計算出下一步所有可能對應的狀態或狀態-動作函數，然后乘以折扣系數，采樣求期望得到下一步迭代新的V′_π（s_t）和Q′_π（s_t，a_t）。如此不斷反復，直到最后對應的函數收斂（兩次迭代的差值小于一定的標準）。從理解上說，可以認為V_π（s_t）和Q_π（s_t，a_t）是對未來回報的一個近似，通過不斷修正這個近似，最終可以讓我們的價值函數和動作-價值函數收斂到正確的數值。