- Moldflow 2021模流分析從入門到精通(升級(jí)版)
- 陳如香等編著
- 1351字
- 2022-05-06 17:13:01
1.1 有限元分析簡(jiǎn)介
AMI采用的基本思想是工程領(lǐng)域中最為常見的有限元法。有限元網(wǎng)格模型如圖1-1所示。有限元法的靈活性很大,對(duì)邊界形狀的描述具有良好的適應(yīng)性,可以模擬復(fù)雜的邊界問題,因而被分析人員青睞。
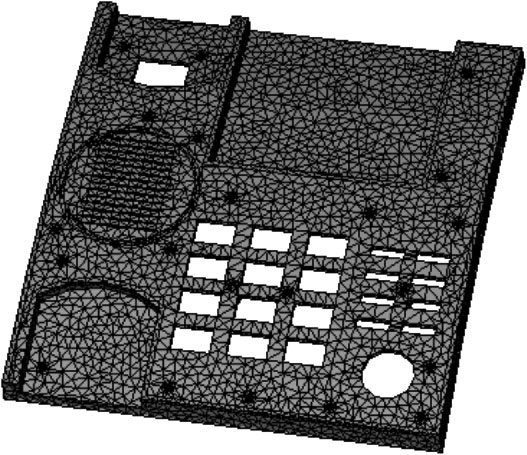
圖1-1 有限元網(wǎng)格模型
有限元法的應(yīng)用從最初的離散彈性系統(tǒng)發(fā)展到連續(xù)介質(zhì)力學(xué)領(lǐng)域,目前廣泛應(yīng)用于工程結(jié)構(gòu)強(qiáng)度、熱傳導(dǎo)、電磁場(chǎng)、流體力學(xué)等領(lǐng)域。經(jīng)過多年的發(fā)展,現(xiàn)在的有限元法幾乎可以用來求解所有的連續(xù)介質(zhì)和場(chǎng)問題,包括靜力問題、與時(shí)間有關(guān)的變化問題及振動(dòng)問題。
1.1.1 有限元法的基本思想
1.?dāng)?shù)理方程的求解方法
數(shù)理方程的求解過程如圖1-2所示。
2.有限元法的基本思想
將一個(gè)連續(xù)的求解域(連續(xù)體)離散化即分割成彼此用節(jié)點(diǎn)(離散點(diǎn))互相聯(lián)系的有限個(gè)單元,如圖1-3所示。在單元體內(nèi)假設(shè)近似解的模式,用有限個(gè)節(jié)點(diǎn)上的未知參數(shù)表征單元的特性,然后用適當(dāng)?shù)姆椒ǎ瑢⒏鱾€(gè)單元的關(guān)系式組合成包含這些未知參數(shù)的代數(shù)方程,得出各節(jié)點(diǎn)的未知參數(shù),再利用插值函數(shù)求出近似解。
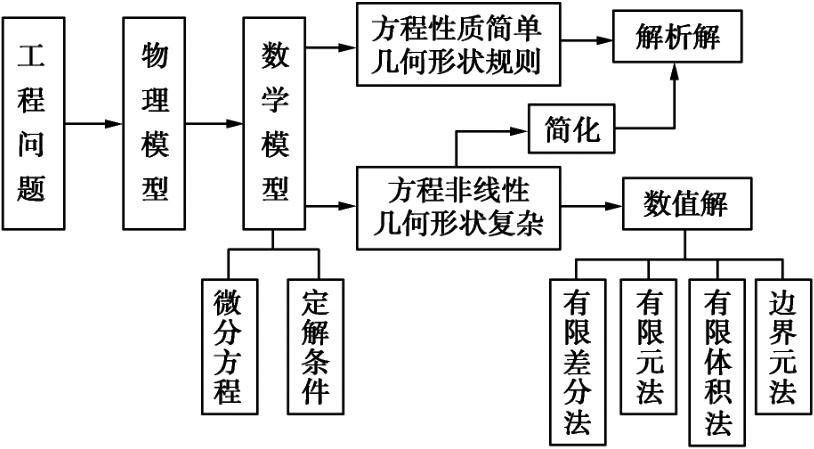
圖1-2 數(shù)理方程的求解過程
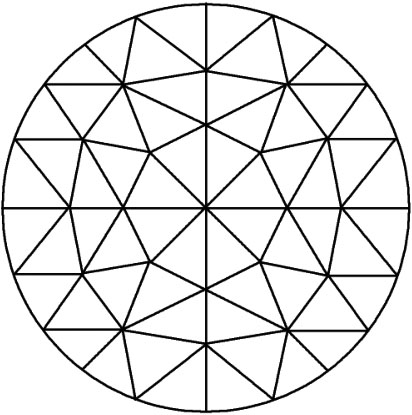
圖1-3 連續(xù)體的離散化
有限元法是一種用有限的單元離散連續(xù)體進(jìn)行求解的數(shù)值計(jì)算的近似方法。由于單元可以分割成各種形狀和尺寸的連續(xù)體,所以它能很好地適應(yīng)復(fù)雜的幾何形狀、材料特性和邊界條件。
由于已有成熟大型軟件系統(tǒng)的支持,有限元法已經(jīng)成為一種非常受歡迎的、應(yīng)用極廣的數(shù)值計(jì)算方法。
(1)特點(diǎn):基于變分原理,建立基本方程和定解條件的積分提法,建立泛函的變分。
(2)求解步驟:將求解域劃分單元,在單元內(nèi)假設(shè)近似分布函數(shù),通過單元分析進(jìn)而建立整個(gè)區(qū)域場(chǎng)量的方程。
(3)應(yīng)用:幾乎所有領(lǐng)域。
(4)優(yōu)點(diǎn):幾何形狀復(fù)雜時(shí),通過合適的網(wǎng)格數(shù)可得到較高的計(jì)算精度。
3.有限元法的基本求解步驟
(1)將連續(xù)體離散成有限個(gè)單元的組合體。
(2)利用單元節(jié)點(diǎn)的場(chǎng)量作為基本未知量,選擇一組插值函數(shù),確定單元內(nèi)相應(yīng)的場(chǎng)量分布。
(3)建立單元內(nèi)節(jié)點(diǎn)的基本未知量與載荷間的平衡方程。
(4)將單元內(nèi)節(jié)點(diǎn)基本未知量的平衡方程集成,得出以節(jié)點(diǎn)為基本未知量的平衡方程組。
(5)求解代數(shù)方程組,得出各節(jié)點(diǎn)的基本未知量。
在彈性力學(xué)問題中,通常采用單元節(jié)點(diǎn)位移作為基本未知量,求出節(jié)點(diǎn)位移后,再計(jì)算單元的應(yīng)力應(yīng)變,這種方法稱為位移型有限元法。若以節(jié)點(diǎn)力為未知參數(shù),先求出節(jié)點(diǎn)處的節(jié)點(diǎn)力,后求位移與應(yīng)力的方法,稱為力型有限元法。
1.1.2 有限元法的特點(diǎn)
1.原理清楚,概念明確
有限元法的原理清楚、概念明確,用戶可以在不同的水平上建立起對(duì)該方法的理解,并且根據(jù)個(gè)人的實(shí)際情況(包括不同學(xué)科、不同的理論基礎(chǔ)等)來安排學(xué)習(xí)的計(jì)劃和進(jìn)度,既可以通過直觀的物理意義來學(xué)習(xí)和使用,也可以從嚴(yán)格的力學(xué)概念和數(shù)學(xué)概念方面進(jìn)行推導(dǎo)。
2.應(yīng)用范圍廣泛,適應(yīng)性強(qiáng)
有限元法可以用來求解工程中許多復(fù)雜的問題,特別是采用其他數(shù)值計(jì)算方法(有限差分法)求解困難的問題,如復(fù)雜結(jié)構(gòu)形狀問題、復(fù)雜邊界條件問題、非均質(zhì)和非線性材料問題、動(dòng)力學(xué)問題、黏彈性流體流動(dòng)問題等。目前,有限元法在理論和應(yīng)用上仍在不斷發(fā)展,今后將更加完善,應(yīng)用也會(huì)更加廣泛。
3.有利于計(jì)算機(jī)應(yīng)用
有限元法采用矩陣形式表達(dá),便于編制計(jì)算機(jī)程序,充分利用高性能計(jì)算機(jī)的計(jì)算優(yōu)勢(shì)。由于有限元法計(jì)算過程的規(guī)范化,目前在國(guó)內(nèi)外有許多通用程序可以直接使用,非常方便。AMI正是成熟的注射成型的有限元工程分析軟件。
- Photoshop+Camera Raw風(fēng)光、人文、城市、星空攝影后期技法(全彩)
- 剪映短視頻制作全流程:剪輯、調(diào)色、字幕、音效
- 數(shù)據(jù)、模型與決策:基于Excel的建模和商務(wù)應(yīng)用
- Word-Excel-PowerPoint 2010三合一從新手到高手(超值版)
- Moldflow模流分析與工程應(yīng)用
- Puppet 2.7 Cookbook
- Illustrator平面設(shè)計(jì)立體化教程:Illustrator 2021(微課版)
- Photoshop CC 2018基礎(chǔ)教程(第3版)
- CorelDRAW X6平面設(shè)計(jì)與制作案例教程
- AI繪畫基礎(chǔ)與商業(yè)實(shí)戰(zhàn)
- 數(shù)碼攝影修圖師完全手冊(cè)(第2卷)
- MSC Fatigue疲勞分析標(biāo)準(zhǔn)教程
- Learn OpenOffice.org Spreadsheet Macro Programming: OOoBasic and Calc automation
- The Oracle Universal Content Management Handbook
- 中文版CINEMA 4D R18 實(shí)用教程