2.4 限失真信源編碼定理

之前討論的都是無失真編碼，為了達到無失真，往往需要花費巨大的代價，同時，在很多種情況下，人們并不需要完全的無失真，接近信源發出的消息就能夠滿足要求。例如，在一塊較小的手機屏幕上，2K分辨率和1K分辨率對于人眼來說并沒有多大區別；用普通耳機聽音樂，高品質音樂和稍低品質的音樂對人的耳朵來講差別也不是很大；看電影時，由于人眼的視覺暫留特點，每秒24幀圖像和36幀圖像觀看感受差別不是很大。但是數據量卻差別很大。這就是說，在許多應用場景下，失真是可以允許的，可以節約很多成本，并大大提高通信的效率。但是在允許失真的前提下，這個失真度如何把握？如何對失真進行描述？信息率失真函數回答了這些問題。香農提出的限失真編碼定理定量地描述了失真，研究了信息率和失真之間的關系，已經成為量化、數據轉換等現代通信技術的理論基礎。本節簡單介紹相關理論的基本原理，以方便讀者后續章節的學習。

2.4.1 信息率失真函數

實際應用中，信號有一定程度的失真是可以容忍的。但是當失真超出某一限度后，信息質量將嚴重受損，甚至無法使用。要規定失真限度，必須先有一個定量的失真測度。因此引入了失真函數的概念。

1.失真函數

設離散無記憶信源X，X={x₁，…，x_r}，其概率分布為P（x）=[P（x₁），…，P（x_r）]。信源符號通過信道傳輸到某接收端，接收端的接收變量Y={y₁，…，y_s}。如圖2-3所示。

對應于每一對（x，y），指定一個非負的函數

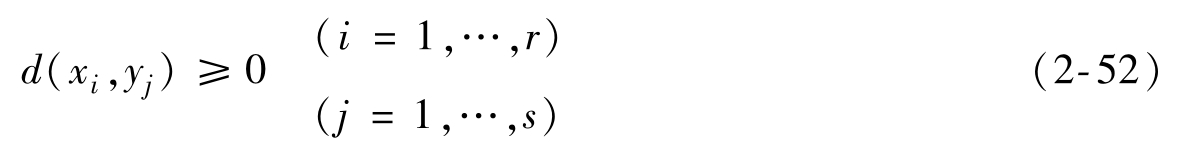
為單個符號的失真函數（失真度），用來測量信源發出一個符號x_i，在接收端收到一個符號y_j所引起的誤差和失真。

很明顯，如果x_i=y_j，說明發送和接收之間沒有失真，故d（x_i，y_j）=0，反之，如果x_i≠y_j，則意味著出現了失真，d（x_i，y_j）的值不為0。

由于信道輸入符號集X={x₁，…，x_r}有r種符號，輸出符號集Y={y₁，…，y_s}有s種符號，因此d（x_i，y_j）就有r×s個。按照x_i（i=1，…，r）和y_j（j=1，…，s）的對應關系，排列為一個r×s矩陣，得到

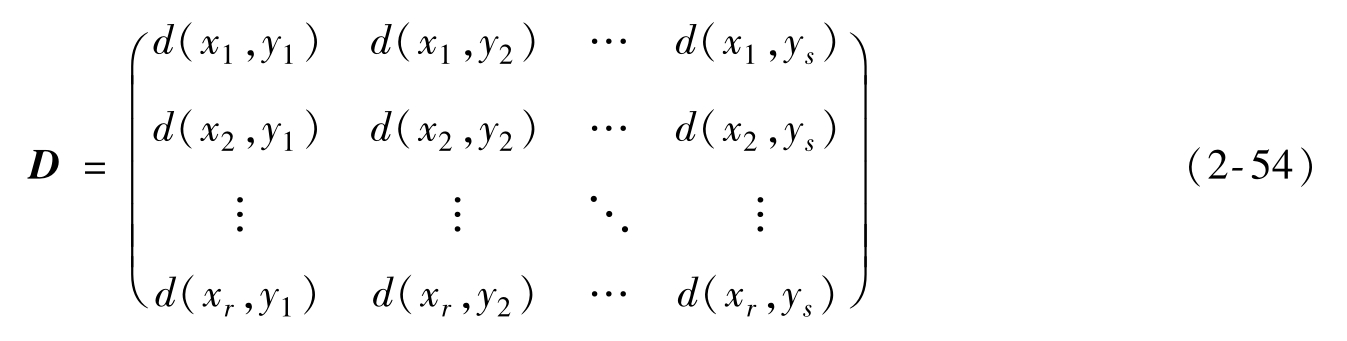
稱之為失真矩陣D。

接下來看幾個常見的失真函數。

（1）漢明失真

信源和信宿的符號集合相同，每個符號的交叉傳輸概率相等，就是說當再現的接收符號與發送的信源符號相同時（i=j），不存在失真，失真度為0；當接收符號與發送符號不同時，失真存在并且都為常數1。即

那么它的失真矩陣為r×r矩陣

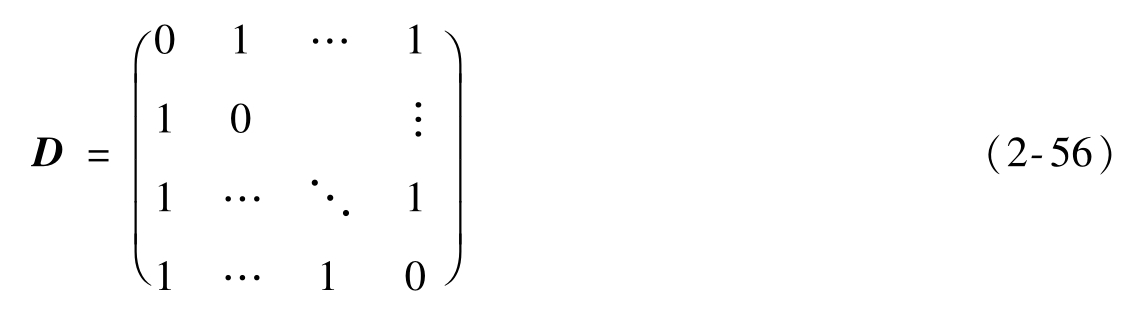
該矩陣具有對稱性，用漢明矩陣來度量失真的信源稱為離散對稱信源。

當r=2時，則為二進制刪除信道，有

它表示發送信源符號0（1）同時接收符號也是0（1）時，認為無失真，反之，發送0（1），接收1（0），則認為有失真并且兩種錯誤等同。

【例2-4】設信道輸入X={0，1}，輸出Y={0，1，2}，失真函數為d（0，0）=d（1，1）=0，d（0，1）=d（1，0）=1，d（0，2）=d（1，2）=0.6，求D。

【解】

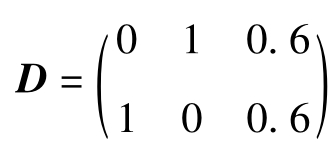
該信道為一個二元刪除信道。

接下來將單符號失真函數推廣到長度為N的信源符號序列失真函數。設信源輸出符號序列X=X₁X₂…X_N，其中每個隨機變量都取值于同一符號集X={x₁，…，x_r}，因此共有r^N個不同的信源符號序列x_i，接收符號序列為Y=Y₁Y₂…Y_N，同樣其中每個隨機變量都取值于同一個符號集Y={y₁，…，y_s}，一共有s^N個不同的接收符號序列y_j。由此可以得出如下定義：

設發送序列為X={x₁，…，x_r}，接收序列為Y={y₁，…，y_s}，那么定義序列的失真度為

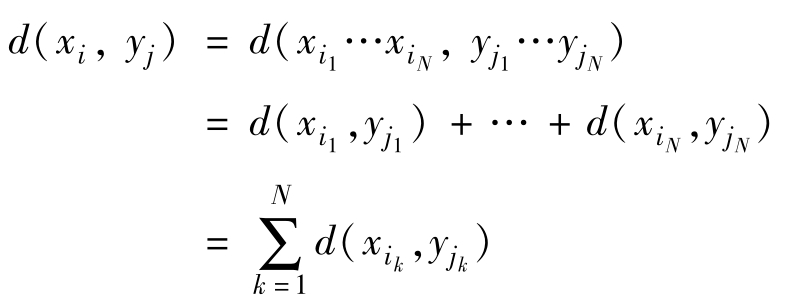
即信源序列的失真度等于序列中對應單個符號失真度之和，不同的（x_i，y_j），其對應的d（x_i，y_j）也不同，矩陣形式的D（N）為r^N×s^N矩陣。

【例2-5】設信源輸出序列X=X₁X₂X₃，其中每個隨機變量均取值于X={0，1}。經過信道傳輸后的輸出為Y=Y₁Y₂Y₃，其中每個隨機變量都取值于Y={0，1}。定義失真函數d（0，0）=d（1，1）=0，d（0，1）=d（1，0）=1，求失真矩陣D（N）。

【解】根據序列失真函數定義，可以得到：

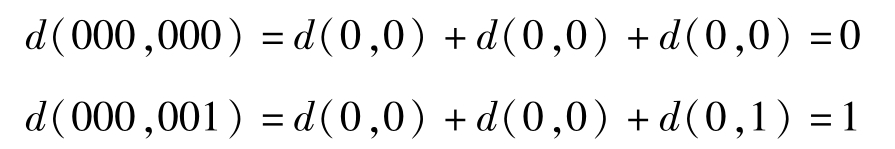
以此類推，可以得到失真矩陣為

（2）平方誤差失真

失真函數定義為

其中i，j=1，2，…，r。其失真矩陣為

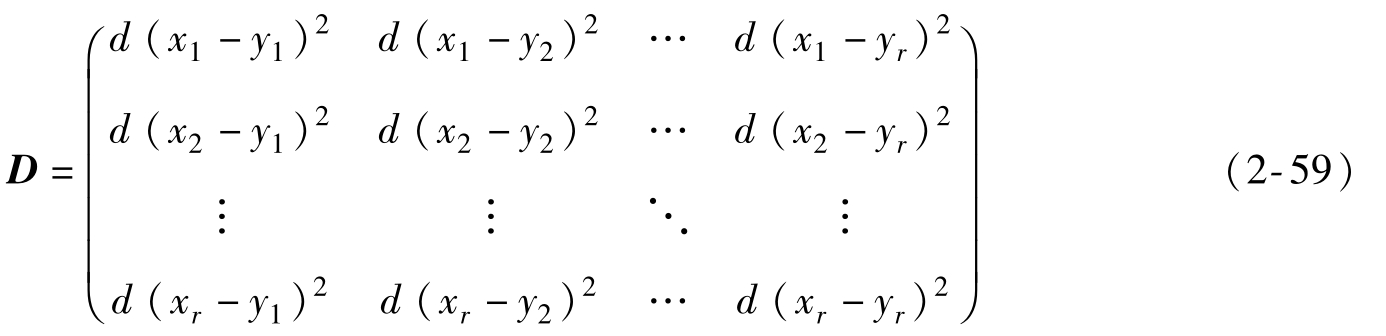
這意味著幅度差值大要比幅度差值小所引發的失真更嚴重。

【例2-6】設信道r=s=3，輸入X={0，1，2}，輸出Y={0，1，2}，求平方誤差失真矩陣D。

【解】

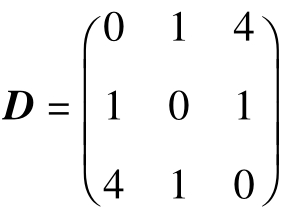
2.平均失真度與保真度準則

d（x_i，y_j）只能表示兩個特定符號x_i和y_j之間的失真，為了表示信道平均每傳遞一個符號所引起失真的大小，定義平均失真度為失真函數的數學期望，即d（x_i，y_j）在X和Y的聯合概率空間P（X|Y）中的統計平均值：

其中，E[·]表示求期望。

如果已知信道傳遞概率為，按照數學期望的定義

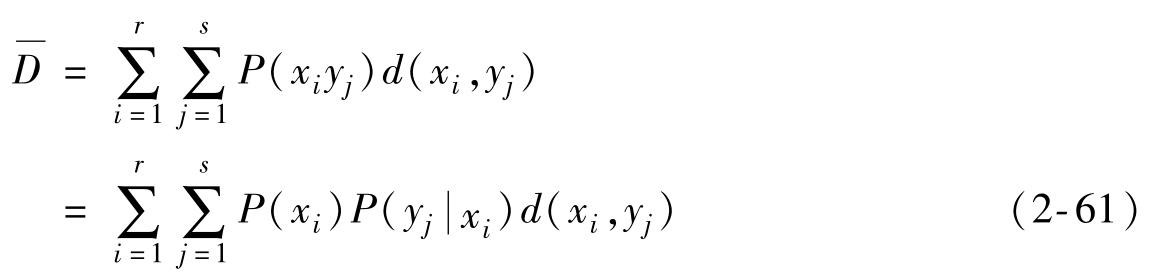
可以看出，平均失真度描述了在平均意義上信源在某一信道傳輸下的失真大小。

上面是單符號信源的失真度和平均失真度。對于單符號離散無記憶信源X={x₁，…，x_r}，其N次擴展信源為X^N=X₁X₂…X_N，在信道中的傳遞作用相當于單符號離散無記憶信道的N次擴展信道，輸出同樣是一個隨機變量序列Y^N=Y₁Y₂…Y_N。其輸入有r^N個不同符號：

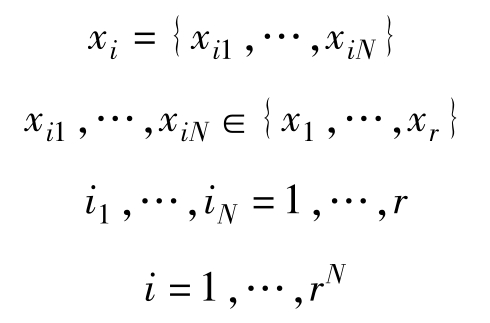
信道輸出共有s^N個不同符號

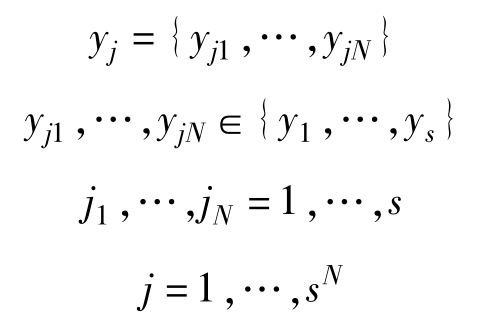
那么N次擴展信道的失真函數為

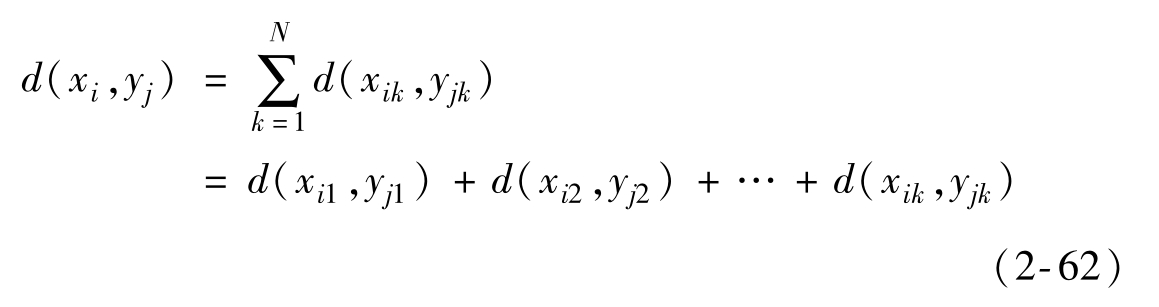
其N次擴展信道的平均失真函數為

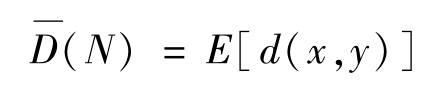
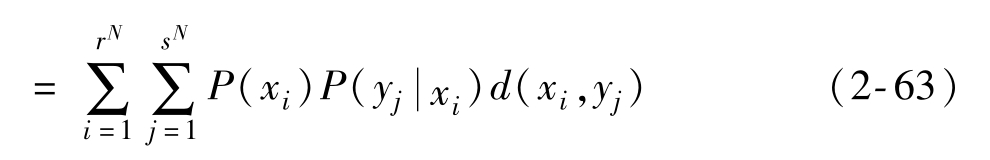
那么單個符號的平均失真度（信源平均失真度）為

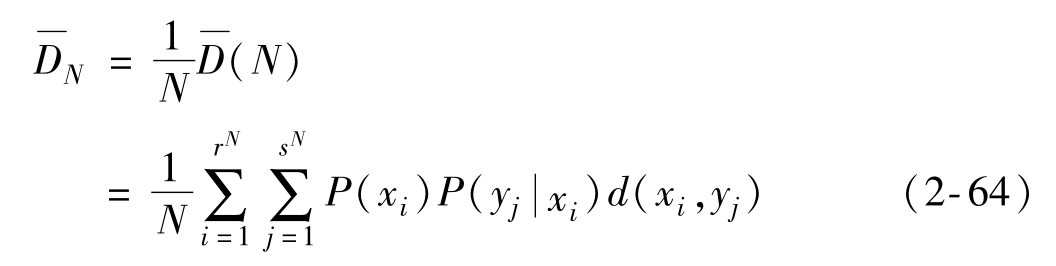
當信源與信道都是無記憶時，N次擴展信源的平均失真度為

其中表示信源序列中第k個分量的平均失真度，如果信源是平穩信源，那么

于是

也就是說，離散無記憶平穩信源通過無記憶信道，其信源序列的平均失真度等于單個符號平均失真度的N倍。

如果平均失真度不大于所允許的失真D，稱之為保真度準則。即：

同樣，N維信源序列的保真度準則如下：

即離散無記憶N次擴展信源通過離散無記憶N次擴展信道的平均失真度不大于單符號信源通過單符號信道的平均失真度的N倍。

3.信息率失真函數

對于單符號信源和單符號信道在信源給定并定義了具體的失真函數以后，人們總希望在滿足一定失真的情況下，使傳送信源必須傳給收信者的信息傳輸率R越小越好，從接收端來看，就是在滿足保真度準則的條件下，尋找再現信源消息所需的最低平均信息量，即平均互信息I（X；Y）的最小值。設B_D是滿足保真度準則的試驗信道集合，由于平均互信息是信道傳遞概率）的下凸函數，因此在B_D集合中，極小值存在，這個最小量，即平均互信息I（X；Y）的最小值。設B_D是滿足保真度準則的試驗信道集合，由于平均互信息是信道傳遞概率P（y_j |x_i）的下凸函數，因此在B_D集合中，極小值存在，這個最小值就是在滿足保真度準則的條件下，信源傳輸的最小平均信息量，稱為信息率失真函數或者率失真函數。其表達式為

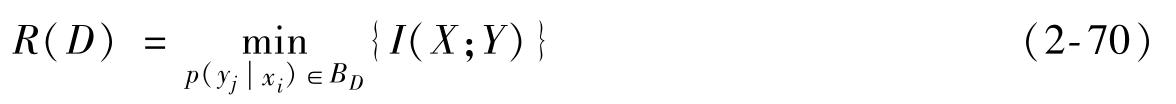
那么對于離散無記憶信源的N次擴展信源和離散無記憶信道的N次擴展信道，其信息率失真函數為

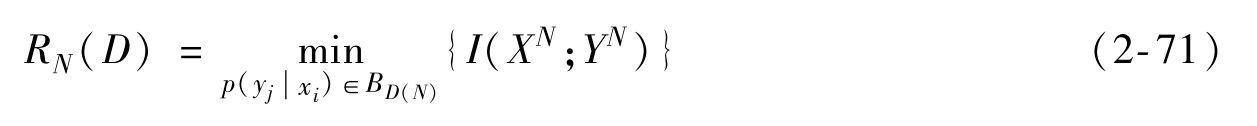
對于離散無記憶平穩信源，可以得到

研究信息率失真函數是希望在已知信源和允許失真度的條件下，使得信源必須傳送給用戶的信息量最小。這個問題就是在一定失真度條件下，盡可能用最少的碼符號來傳送信源消息，使信源消息盡快傳送出去，以提高通信的有效性。

（1）離散信源的信息率失真函數

對于基本離散信源來說，求信息率失真函數與求信道容量類似，都是在有約束條件下求平均互信息極值的問題，區別在于不同的約束條件。信道容量是求平均互信息的條件極大值，而信息率失真函數是求平均互信息的條件極小值。

已知信源概率分布函數p（x_i）和失真函數d（x_i，y_i），在滿足保真度準則的條件下，一般試驗信道P_D當中選擇，使平均互信息

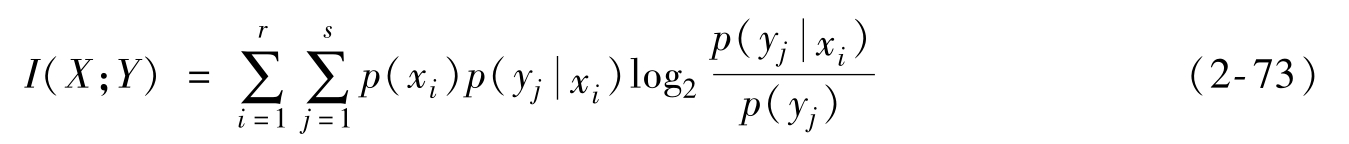
值最小，并且使

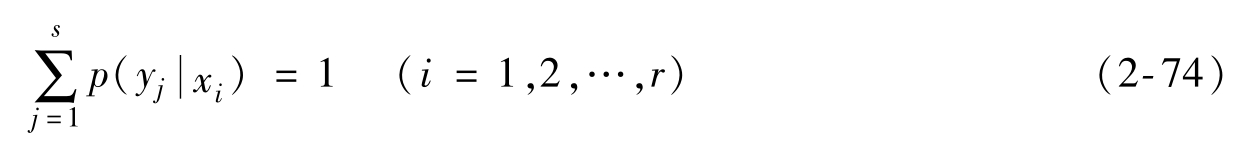
以及

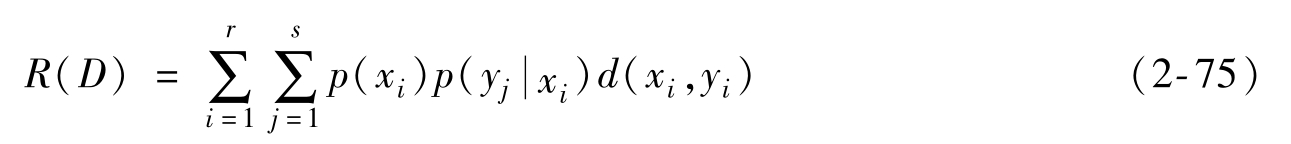
（2）連續信源的信息率失真函數

按照離散信源失真函數、平均失真函數和信息率失真函數的定義，定義連續信源平均失真度為

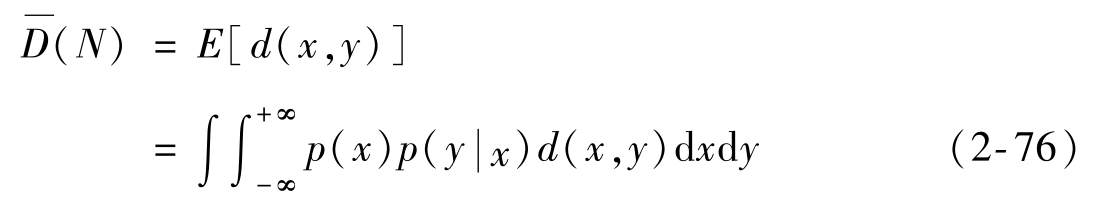
式中，d（x，y）為連續信源失真函數，p（x）為連續信源X的概率密度，）為信道傳遞式中，d（x，y）為連續信源失真函數，p（x）為連續信源X的概率密度，p（y|x）為信道傳遞概率密度。

平均互信息為

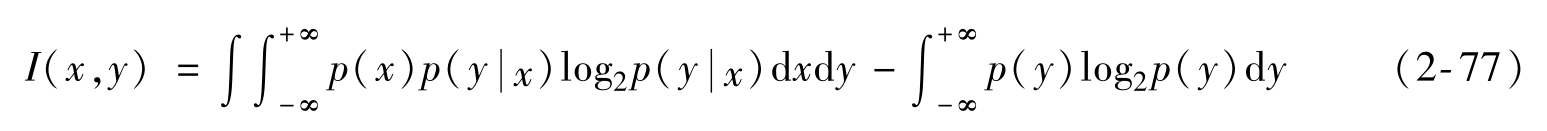
式中

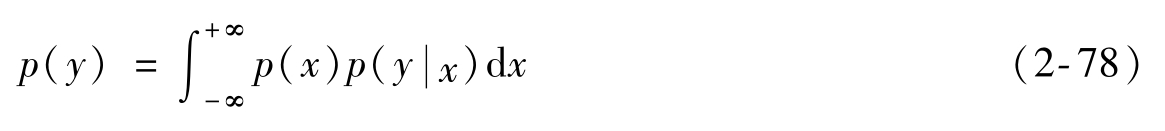
并且

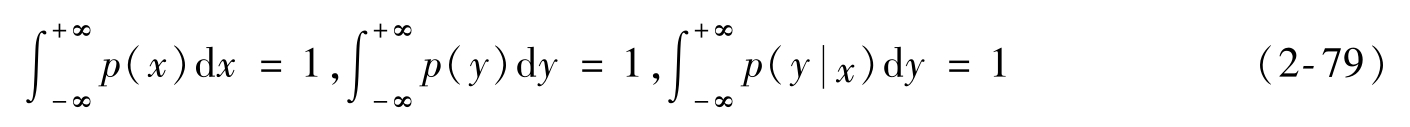
定義B_D是滿足保真度準則的所有廣義無擾信道集合，那么連續信源信息率失真函數為

式中，Inf指下確界，相當于離散信源中求極小值，連續集合中可能不存在極小值，但是一定存在下確界。所謂下確界，是在“下界”的基礎上定義的，指的是任一數集E，我們稱E的最大下界為E的下確界。

2.4.2 限失真信源編碼定理

設離散無記憶信源的輸出變量序列為X=（X₁X₂…X_L），該信源失真函數為R（D），并選定有限失真函數，對于任意允許平均失真度D≥0，和任意小的ε＞0，當信息率

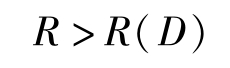
只要信源序列長度L足夠長，一定存在一種編碼方法C，使其譯碼后的平均失真小于或等于D+ε，即

反之，若

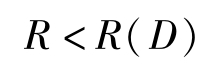
則無論采用什么樣的編碼方法，其平均譯碼失真必大于D，即

這就是限失真信源編碼定理，又稱為保真度準則下的離散信源編碼定理。該定理可以推廣到連續平穩無記憶信源的情況，證明略。

可以看出，信息率失真函數R（D）是在允許失真度為D的情況下信源信息壓縮的下限。當信源給定后，無失真信源壓縮的極限值是信源熵H（S）；而限失真信源壓縮極限值是信息率失真函數R（D）。