- 優(yōu)化驅(qū)動的設(shè)計(jì)方法
- 高亮 邱浩波 肖蜜 李好
- 9006字
- 2021-12-10 16:41:17
3.1 多工況結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)
3.1.1 多工況結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)的擴(kuò)展最優(yōu)性
目前在拓?fù)鋬?yōu)化領(lǐng)域,多數(shù)的設(shè)計(jì)對象都是圍繞單工況結(jié)構(gòu)展開的,也就是在結(jié)構(gòu)設(shè)計(jì)域中只考慮一種載荷工況。然而在實(shí)際工程結(jié)構(gòu)的設(shè)計(jì)過程中,外部工作環(huán)境條件往往比較復(fù)雜,因此需要考慮適應(yīng)多種變化的工況作用,應(yīng)針對不同的工況載荷目標(biāo)設(shè)計(jì)不同的支撐方式以滿足多種功能需求。因此,對多工況下的結(jié)構(gòu)拓?fù)鋬?yōu)化問題進(jìn)行研究更具有工程意義和實(shí)用價值。針對多工況下結(jié)構(gòu)拓?fù)鋬?yōu)化問題,需要權(quán)衡多條剛度分布路徑,亦可稱為多剛度拓?fù)鋬?yōu)化問題。需要特別注意的是,多工況拓?fù)鋬?yōu)化問題與多載荷拓?fù)鋬?yōu)化問題是兩個不同的問題,兩者最大的區(qū)別在于不同載荷的施加是否一致:多工況拓?fù)鋬?yōu)化問題中各類載荷不是同時加載,而多載荷拓?fù)鋬?yōu)化問題中的所有載荷則是同時施加。這便意味著多工況拓?fù)鋬?yōu)化問題的本質(zhì)為一種多目標(biāo)優(yōu)化問題。
在經(jīng)典的結(jié)構(gòu)拓?fù)鋬?yōu)化問題中,將結(jié)構(gòu)在外載荷作用下剛度最大化作為優(yōu)化目標(biāo)函數(shù)是比較常見的算例。除此之外,通常還會根據(jù)設(shè)計(jì)者的經(jīng)驗(yàn)對結(jié)構(gòu)減重百分比(即體積比分?jǐn)?shù))進(jìn)行預(yù)估,并將其作為優(yōu)化模型中的約束條件(或者以最小體積作為優(yōu)化目標(biāo),將預(yù)估的結(jié)構(gòu)剛度值作為約束條件),見式(3-1)和式(3-2)。也就是說,傳統(tǒng)拓?fù)鋬?yōu)化方法的設(shè)計(jì)結(jié)果實(shí)際上有部分程度還需依賴于設(shè)計(jì)者的先驗(yàn)知識。由此可見,其與創(chuàng)新設(shè)計(jì)的自動化與智能化的理念存在矛盾。
問題1 以結(jié)構(gòu)剛度最大化(通常以柔度C最小化表示)為優(yōu)化目標(biāo),結(jié)構(gòu)體積V不超過預(yù)估體積V0為約束條件:

問題2 以結(jié)構(gòu)體積V最小化為優(yōu)化目標(biāo),結(jié)構(gòu)柔度C不超過預(yù)估值C0為約束條件:

目前已經(jīng)有眾多學(xué)者針對單目標(biāo)優(yōu)化問題進(jìn)行了相關(guān)研究,所采用的方法為:對結(jié)構(gòu)的剛度和體積同時優(yōu)化,并將該類優(yōu)化問題命名為拓?fù)鋬?yōu)化中的“擴(kuò)展最優(yōu)性(extended optimality)”。2002年,擴(kuò)展最優(yōu)性的概念由Rozvany等[1]首次提出,該工作主要針對的是二維結(jié)構(gòu)和單工況結(jié)構(gòu)。該方法的基本思想是通過優(yōu)化不同結(jié)構(gòu)性能指標(biāo)的乘積,來實(shí)現(xiàn)各指標(biāo)的聯(lián)合優(yōu)化,如式(3-3)。隨后,Rozvany[2]對比了傳統(tǒng)拓?fù)鋬?yōu)化設(shè)計(jì)與具有擴(kuò)展最優(yōu)性拓?fù)鋬?yōu)化設(shè)計(jì)結(jié)果,指出引入擴(kuò)展最優(yōu)性能夠得到重量較輕的設(shè)計(jì)方案。相較于乘積形式的目標(biāo)函數(shù)f=CV,Str?mberg[3]提出了一種更加通用的目標(biāo)函數(shù)f=CVη,在該目標(biāo)函數(shù)中,可以通過改變參數(shù)η的值,來獲取更多不同的可選優(yōu)化設(shè)計(jì)結(jié)果。上述研究均采用了基于SIMP材料插值模型的拓?fù)鋬?yōu)化設(shè)計(jì)方法。實(shí)際上這種優(yōu)化概念同樣可以應(yīng)用到其他類型的拓?fù)鋬?yōu)化方法,如ESO方法等:Tanskanen[4]從理論角度對拓?fù)鋬?yōu)化設(shè)計(jì)中的擴(kuò)展最優(yōu)性展開了深入的討論,Edwards等[5]則對比了ESO方法和SIMP方法在解決考慮擴(kuò)展最優(yōu)性的結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)問題上的優(yōu)缺點(diǎn)。值得注意的是,以上全部研究主要是采用了乘積形式的目標(biāo)函數(shù),且主要是用于解決單工況結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)問題。
問題3 以結(jié)構(gòu)柔度C與結(jié)構(gòu)體積V的乘積為目標(biāo)函數(shù),同時對兩項(xiàng)結(jié)構(gòu)指標(biāo)進(jìn)行優(yōu)化,即所謂的“擴(kuò)展最優(yōu)性”:

通過上述論述可以看出,擴(kuò)展最優(yōu)性的提出主要是為了更好地應(yīng)對工程結(jié)構(gòu)輕量化設(shè)計(jì)需求,這種設(shè)計(jì)概念不需要設(shè)計(jì)者在優(yōu)化開始時就根據(jù)經(jīng)驗(yàn)給出結(jié)構(gòu)剛度或體積分?jǐn)?shù)的預(yù)估值,而是通過求解優(yōu)化問題來自動得到更加豐富且更加輕質(zhì)的設(shè)計(jì)方案。可見,考慮擴(kuò)展最優(yōu)性的多工況結(jié)構(gòu)拓?fù)鋬?yōu)化問題建模與求解方法的建立就具有十分重要的理論意義和工程價值。接下來,本節(jié)將對上述問題進(jìn)行重點(diǎn)論述。
3.1.2 多目標(biāo)拓?fù)鋬?yōu)化模型
對于多工況結(jié)構(gòu)拓?fù)鋬?yōu)化問題來說,至關(guān)重要的一點(diǎn)就是通過構(gòu)建合適的多目標(biāo)優(yōu)化模型,使其能夠搜尋整個Pareto最優(yōu)前端。理論上,Pareto最優(yōu)的充分/必要條件是判斷能否通過某種特定的多目標(biāo)模型求解出整個Pareto最優(yōu)解集的關(guān)鍵[6]。一方面,當(dāng)多目標(biāo)優(yōu)化模型滿足Pareto最優(yōu)的必要條件時,通過該模型能夠解出全部的Pareto最優(yōu)解,但其中部分解可能不是Pareto最優(yōu)解;另一方面,當(dāng)多目標(biāo)優(yōu)化模型滿足Pareto最優(yōu)解的充分條件時,通過該模型解出的全部解均為Pareto最優(yōu)解,但其無法求出整個Pareto解集。也就是說,當(dāng)選擇一種合適的多目標(biāo)優(yōu)化模型,使其滿足Pareto最優(yōu)解的充要條件,通過該模型就一定能求解出整個Pareto最優(yōu)前端上的解。在多工況拓?fù)鋬?yōu)化設(shè)計(jì)領(lǐng)域,因?yàn)閮?yōu)化模型的設(shè)計(jì)變量多,學(xué)者們通常采用直接加權(quán)法來處理多個載荷工況下的子目標(biāo)函數(shù),但無論如何選擇子目標(biāo)權(quán)重,都無法在優(yōu)化問題Pareto前端非凸的情況下找到其全部Pareto最優(yōu)解集[7]。這也就意味著,針對某些多工況拓?fù)鋬?yōu)化問題,如果設(shè)計(jì)者改變子目標(biāo)重要程度偏好,就可能會導(dǎo)致無法獲得相應(yīng)的Pareto最優(yōu)解的問題。
指數(shù)加權(quán)準(zhǔn)則(exponential weighting criterion,EWC)是一種在理論上被證明的、能夠滿足Pareto最優(yōu)充要條件的多目標(biāo)模型。[6],[8],[9]通過該模型,無論多目標(biāo)問題的Pareto最優(yōu)前端是否非凸,都可憑借連續(xù)地改變子目標(biāo)權(quán)重來獲取全部的Pareto最優(yōu)解集。基于EWC的多目標(biāo)優(yōu)化模型可以表述為
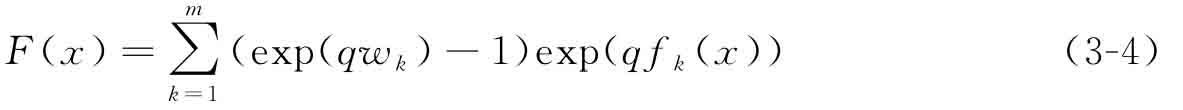
其中,wk為權(quán)重系數(shù);m代表子目標(biāo)的個數(shù);子目標(biāo)fk(x)通過指數(shù)加權(quán)的方式轉(zhuǎn)化為統(tǒng)一的單目標(biāo)F(x);指數(shù)常數(shù)q為實(shí)數(shù),在這里取q=2,以保證模型能夠找到多工況拓?fù)鋬?yōu)化問題的整個Pareto最優(yōu)前端。
需要注意的是,在采用模型(3-4)中所定義的目標(biāo)函數(shù)時,q和fk(x)通常作為指數(shù),如果取值較大,極易造成計(jì)算數(shù)值過大甚至數(shù)值溢出(numerical overflow)。此外,當(dāng)各子目標(biāo)的數(shù)量級顯著不同時,最優(yōu)設(shè)計(jì)一定會更容易受到量級較大的目標(biāo)影響,從而出現(xiàn)“載荷病態(tài)”的情況發(fā)生。因此,需要對基于EWC的多目標(biāo)優(yōu)化設(shè)計(jì)模型進(jìn)行進(jìn)一步的改進(jìn)。本書提出一種基于歸一化指數(shù)加權(quán)準(zhǔn)則(normalized exponential weighting criterion,NEWC)的多目標(biāo)拓?fù)鋬?yōu)化設(shè)計(jì)模型。利用基于水平集的結(jié)構(gòu)邊界隱式描述方式,引入徑向基函數(shù)插值中的擴(kuò)展系數(shù)α作為設(shè)計(jì)變量,可以得到基于參數(shù)化水平集的優(yōu)化模型:
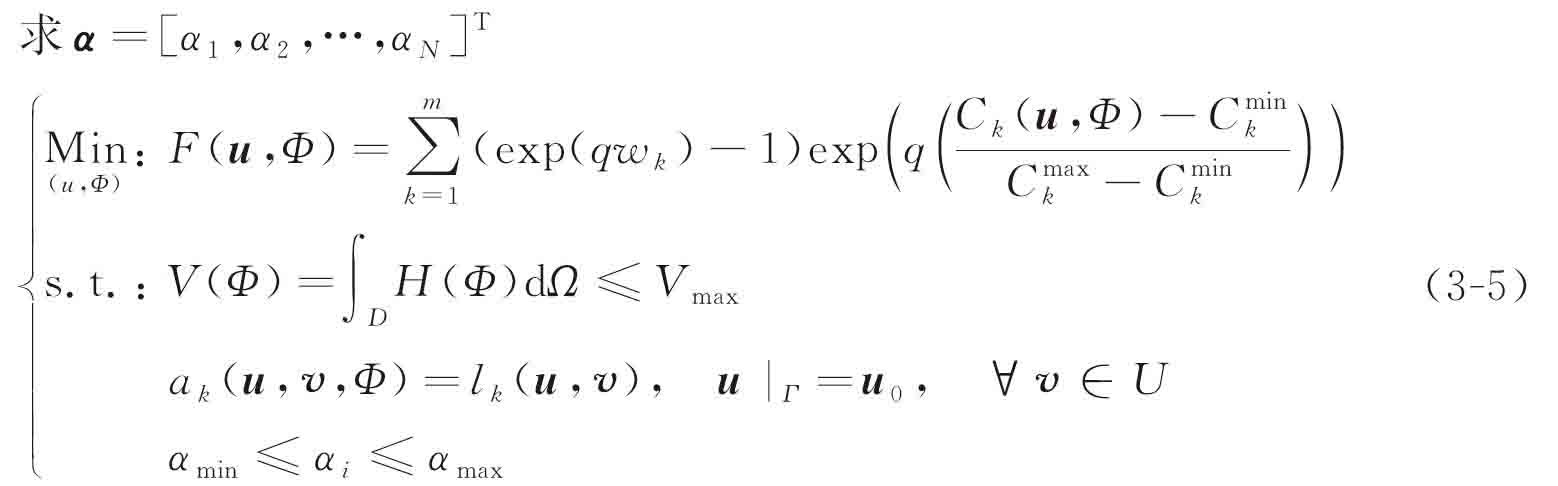
其中,Ck(u,Φ)為子工況k作用下的結(jié)構(gòu)應(yīng)變能:
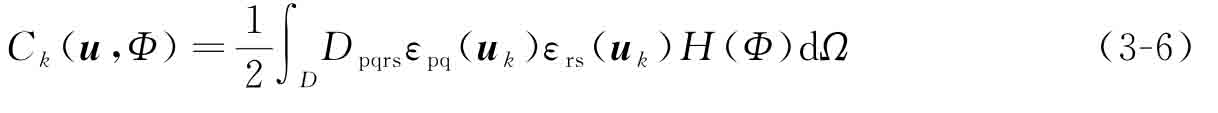
ak(u,v,Φ)為子工況k的能量雙線性形式:
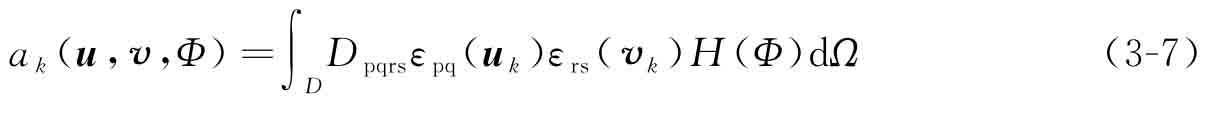
lk(v,Φ)為子工況k的載荷線性形式:
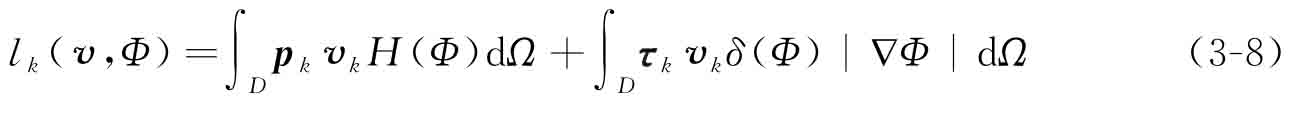
其中,Dpqrs為材料的彈性張量;m為所考慮的工況數(shù)量;N為有限元單元數(shù)量;Vmax為體積約束值;u0為Dirichlet邊界上的位移;H(Φ)為Heaviside函數(shù);δ(Φ)為Heaviside函數(shù)的偏導(dǎo)數(shù),即Dirac函數(shù)。αmax和αmin分別為設(shè)計(jì)變量的上下限,主要用于增加優(yōu)化迭代的穩(wěn)定性。對于任意子工況k,uk和vk分別表示實(shí)位移場和運(yùn)動學(xué)允許的位移空間U內(nèi)的虛位移場,ε為應(yīng)變場,pk為結(jié)構(gòu)體積力,τk為結(jié)構(gòu)邊界上的牽引力,  分別代表單工況k作用下的目標(biāo)函數(shù)最小值與最大值,其值可通過分別求解單工況作用下的拓?fù)鋬?yōu)化設(shè)計(jì)問題來預(yù)估得到。與目標(biāo)函數(shù)式(3-4)相比,多目標(biāo)拓?fù)鋬?yōu)化設(shè)計(jì)模型式(3-5)將各個子目標(biāo)值進(jìn)行了歸一化處理,以便有效消除由于各子工況載荷作用下的結(jié)構(gòu)應(yīng)變能數(shù)量級差距過大而引起的載荷病態(tài)情況。此外,歸一化處理后的目標(biāo)函數(shù)值被限定在一個較小的區(qū)間內(nèi),能夠有效克服優(yōu)化計(jì)算時的數(shù)值溢出問題。
分別代表單工況k作用下的目標(biāo)函數(shù)最小值與最大值,其值可通過分別求解單工況作用下的拓?fù)鋬?yōu)化設(shè)計(jì)問題來預(yù)估得到。與目標(biāo)函數(shù)式(3-4)相比,多目標(biāo)拓?fù)鋬?yōu)化設(shè)計(jì)模型式(3-5)將各個子目標(biāo)值進(jìn)行了歸一化處理,以便有效消除由于各子工況載荷作用下的結(jié)構(gòu)應(yīng)變能數(shù)量級差距過大而引起的載荷病態(tài)情況。此外,歸一化處理后的目標(biāo)函數(shù)值被限定在一個較小的區(qū)間內(nèi),能夠有效克服優(yōu)化計(jì)算時的數(shù)值溢出問題。
在結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)中考慮擴(kuò)展最優(yōu)性,其最直接的目的是充分發(fā)掘結(jié)構(gòu)材料的承載潛力,以獲得材料用量更少、更加輕質(zhì)的結(jié)構(gòu)構(gòu)型。如上文所述,目前的所有研究中,學(xué)者們主要采用f=CV或f=CVη這一類乘積形式的單目標(biāo)函數(shù),而該目標(biāo)函數(shù)產(chǎn)生可行解的多樣性有限,并沒能足夠有效地?cái)U(kuò)大解空間。根據(jù)工程經(jīng)驗(yàn)可知,結(jié)構(gòu)的柔度和體積是一對相矛盾的指標(biāo),即提升其中一個的數(shù)值,必將會導(dǎo)致另外一個的數(shù)值降低。故考慮擴(kuò)展最優(yōu)性的拓?fù)鋬?yōu)化問題本質(zhì)應(yīng)為一個多目標(biāo)優(yōu)化問題,不同柔度和體積的組合代表了解空間內(nèi)所對應(yīng)的Pareto最優(yōu)解[10]。這里是將擴(kuò)展最優(yōu)性引入多工況結(jié)構(gòu)拓?fù)鋬?yōu)化設(shè)計(jì)問題中,并構(gòu)建一種更具普遍性的多目標(biāo)優(yōu)化模型:
求α=[α1,α2,…,αN]T
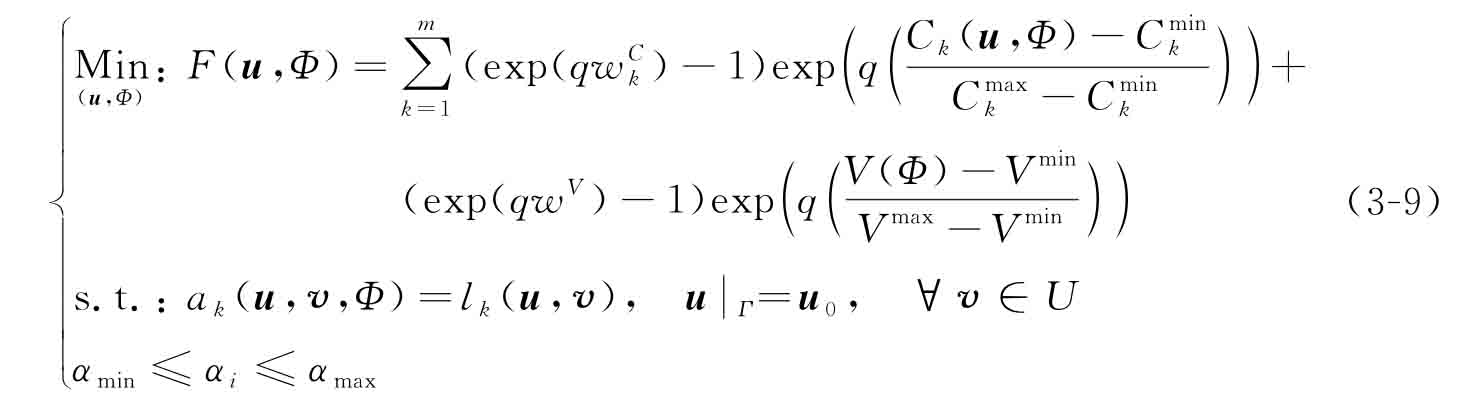
其中,Vmin和Vmax分別代表體積分?jǐn)?shù)約束的最小值與最大值,在本書中設(shè)置為Vmin=0.05和Vmax=1。需要指出的是,由于Vmin取值為0代表結(jié)構(gòu)域內(nèi)沒有任何材料,沒有任何實(shí)際工程意義,故Vmin通常取值為趨近于0的一個較小值。權(quán)重向量  代表各子工況作用下的結(jié)構(gòu)應(yīng)變能及結(jié)構(gòu)整體體積分?jǐn)?shù)的權(quán)重,根據(jù)多目標(biāo)優(yōu)化模型的要求,所有權(quán)重系數(shù)之和設(shè)置為1。
代表各子工況作用下的結(jié)構(gòu)應(yīng)變能及結(jié)構(gòu)整體體積分?jǐn)?shù)的權(quán)重,根據(jù)多目標(biāo)優(yōu)化模型的要求,所有權(quán)重系數(shù)之和設(shè)置為1。
如上所述,構(gòu)建了一套考慮擴(kuò)展最優(yōu)性的多工況拓?fù)鋬?yōu)化模型。在該多目標(biāo)拓?fù)鋬?yōu)化設(shè)計(jì)模型中,所有不同類型的子目標(biāo)函數(shù)均實(shí)施了無量綱化操作,通過NEWC方法轉(zhuǎn)化為單一優(yōu)化目標(biāo),有利于多設(shè)計(jì)變量、大規(guī)模的工程優(yōu)化設(shè)計(jì)問題求解。通過連續(xù)地改變權(quán)重參數(shù),可以得到多套不同的輕量化設(shè)計(jì)方案,甚至多目標(biāo)拓?fù)鋬?yōu)化問題的整個Pareto前端[6]。
3.1.3 目標(biāo)函數(shù)權(quán)重決策方法
在本節(jié)中,將介紹基于模糊多屬性群決策(fuzzy mult-iattribute group descision making,F(xiàn)MAGDM)的決策方法計(jì)算多目標(biāo)拓?fù)鋬?yōu)化模型式(3-9)的權(quán)重系數(shù)。為了得到更可靠的方案,減少錯誤決策的風(fēng)險,人們在進(jìn)行決策活動時通常會兼顧和集中多個專家的意見,這就是所謂的群決策。由于客觀事物的不確定性、不完全性以及人類思維的模糊性,導(dǎo)致大多數(shù)多屬性群決策(mult-iattribute group decisionmaking,MAGDM)問題具有不確定性和隨意性,故而形成了FMAGDM理論。隨著Bellman和Zadeh[11]在1970年首次利用模糊數(shù)學(xué)知識給出模糊決策的基本模型,處理具有不確定性的參數(shù)、概念和事件,基于模糊集理論(fuzzy set theory)的FMAGDM獲得了國內(nèi)外學(xué)者的廣泛關(guān)注[12]。在FMAGDM理論框架中,專家采用語言術(shù)語(linguis ticterms)來描述待決策對象的屬性,然后將語言術(shù)語翻譯成相應(yīng)的模糊數(shù)并進(jìn)行特定的模糊數(shù)計(jì)算、集結(jié)等操作,最終獲得專家的一致性評價意見。對多目標(biāo)拓?fù)鋬?yōu)化問題而言,由于人的偏好以及設(shè)計(jì)方案與權(quán)重系數(shù)間的關(guān)系均具有模糊性,設(shè)計(jì)人員在確定子目標(biāo)權(quán)重系數(shù)時,很難直接給出具體的數(shù)值。所以要求設(shè)計(jì)人員對各子工況下的結(jié)構(gòu)柔度和結(jié)構(gòu)體積指標(biāo)給出諸如“比較重要”“不重要”等之類的評價語言,是一種相對切合實(shí)際的做法。FMAGDM恰好符合這種評價方式,也就是通過模糊的語言術(shù)語來描述對各個子目標(biāo)重要程度的偏好。在對優(yōu)化模型式(3-9)的子目標(biāo)權(quán)重系數(shù)進(jìn)行評估的過程中,子目標(biāo)被視為待決策的“屬性”,設(shè)計(jì)人員被視為“決策者”,并根據(jù)以往積累的工程實(shí)踐先驗(yàn)知識對子目標(biāo)給出語義形式的偏好。
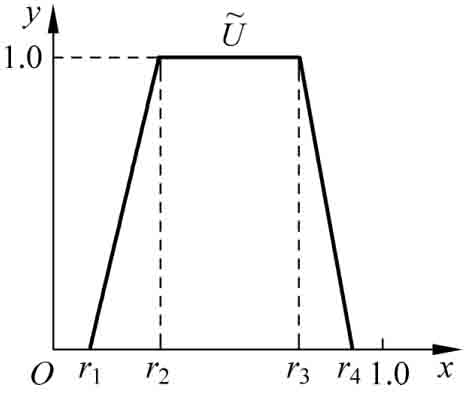
圖3-1 典型的梯形模糊數(shù)
采用圖3-1所示的梯形模糊數(shù)(trapezoidal fuzzy number)[13],[14]來處理權(quán)重系數(shù)計(jì)算過程中的模糊信息。假設(shè)有n個設(shè)計(jì)者D=(D1,D2,…,Dn)對m個優(yōu)化子目標(biāo)O=(O1,O2,…,Om)進(jìn)行評估。其中偏好矩陣E包含m×n個梯形模糊數(shù)  ={eij1,eij2,eij3,eij4},且
={eij1,eij2,eij3,eij4},且  代表設(shè)計(jì)者Dj對子目標(biāo)Oi的偏好。特別地,多數(shù)FMAGDM方法并未考慮到?jīng)Q策者自身的知識水平對決策結(jié)果的影響,在所提出的方法中將另外采用語言術(shù)語描述決策者的等級。反映設(shè)計(jì)者重要程度及能力水平的等級矩陣記為ω={ω1,ω2,…,ωm},其中設(shè)計(jì)者Dj的等級可解釋為梯形模糊數(shù)ω1=(ωj1,ωj2,ωj3,ωj4)。這樣能保證較重要的設(shè)計(jì)者偏好對最終決策結(jié)果起較大作用,反之亦然。
代表設(shè)計(jì)者Dj對子目標(biāo)Oi的偏好。特別地,多數(shù)FMAGDM方法并未考慮到?jīng)Q策者自身的知識水平對決策結(jié)果的影響,在所提出的方法中將另外采用語言術(shù)語描述決策者的等級。反映設(shè)計(jì)者重要程度及能力水平的等級矩陣記為ω={ω1,ω2,…,ωm},其中設(shè)計(jì)者Dj的等級可解釋為梯形模糊數(shù)ω1=(ωj1,ωj2,ωj3,ωj4)。這樣能保證較重要的設(shè)計(jì)者偏好對最終決策結(jié)果起較大作用,反之亦然。
盡管FMAGDM理論的方法對處理含有模糊信息的語言術(shù)語有效,但這種基于專家知識的決策方法仍然帶有一定的主觀隨意性。為了使多目標(biāo)權(quán)重系數(shù)能夠更加準(zhǔn)確地反映實(shí)際工程需求,將根據(jù)客觀歷史數(shù)據(jù)或?qū)嶒?yàn)結(jié)果對子目標(biāo)的取值加以限定,從而構(gòu)建一種自適應(yīng)權(quán)重調(diào)整機(jī)制,以確保避免因主觀偏好的誤差導(dǎo)致優(yōu)化的結(jié)果不準(zhǔn)確。綜上,所提出的基于FMAGDM理論的權(quán)重計(jì)算方法基本步驟如下:
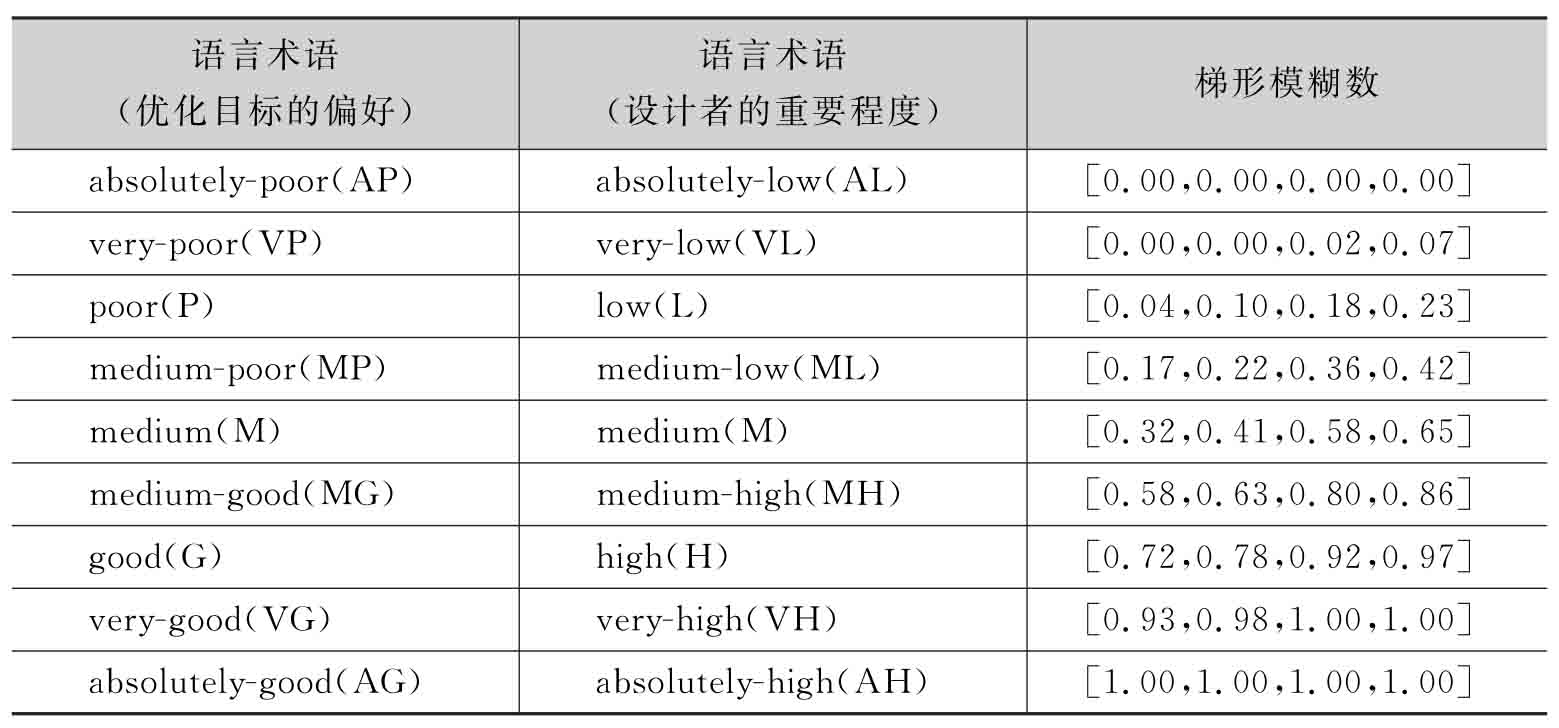
步驟1 設(shè)計(jì)人員對子目標(biāo)采用語言術(shù)語進(jìn)行評價,并將給出的評價矩陣E和專家等級矩陣ω譯為對應(yīng)的梯形模糊數(shù)。從表述最低等級的語言術(shù)語“AP”或“AL”到描述最高等級的語言術(shù)語“AG”或“AH”,每一項(xiàng)語言形式的偏好都有與其唯一對應(yīng)的梯形模糊數(shù)[15],如表3-1所示。
表3-1 語言術(shù)語及其對應(yīng)的梯形模糊數(shù)
步驟2 采用梯形模糊數(shù)混合集結(jié)算子(trapezoidal fuzzy number hybrid aggregation operator,THA)評估偏好  ,從而得到綜合考慮了每位設(shè)計(jì)人員意見及其等級的子目標(biāo)偏好
,從而得到綜合考慮了每位設(shè)計(jì)人員意見及其等級的子目標(biāo)偏好  :
:
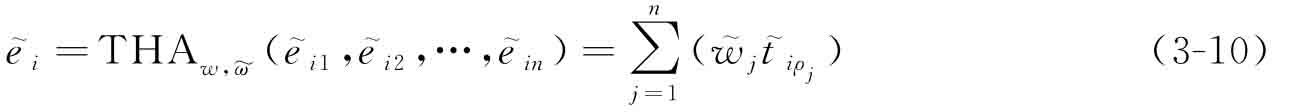
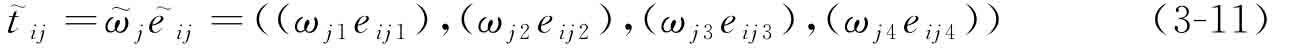
其中,  代表設(shè)計(jì)者Dj對子目標(biāo)Oi的加權(quán)偏好意見;
代表設(shè)計(jì)者Dj對子目標(biāo)Oi的加權(quán)偏好意見;  為
為  從大到小排序后的第j個模糊數(shù);式(3-10)中的權(quán)重系數(shù)
從大到小排序后的第j個模糊數(shù);式(3-10)中的權(quán)重系數(shù)  由下述公式計(jì)算[16]:
由下述公式計(jì)算[16]:
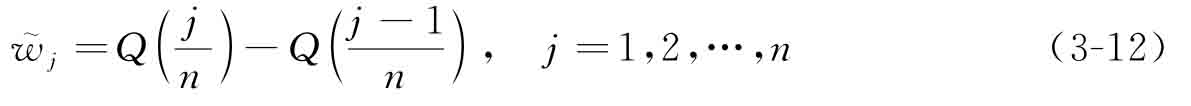
其中,定量模糊語義算子Q由一種分段函數(shù)形式給出:
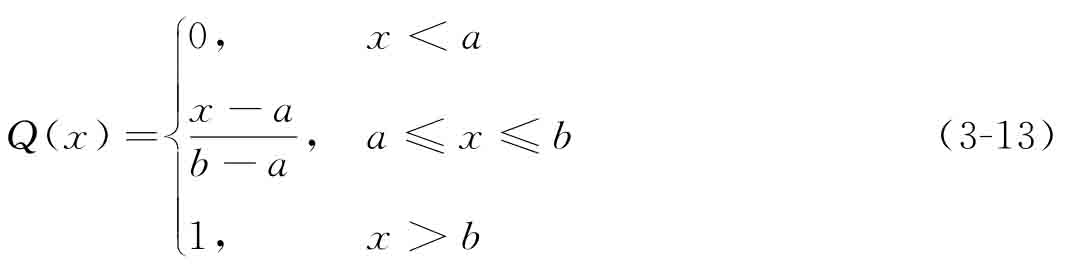
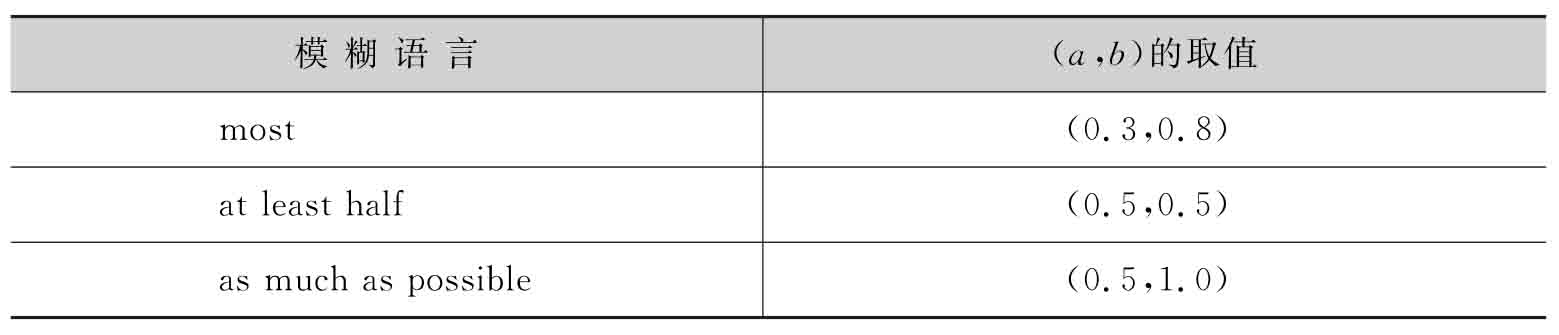
式中的參數(shù)a和b由表3-2中列出的模糊語言定量法則確定。
表3-2 模糊語言定量法則
步驟3 計(jì)算各子目標(biāo)綜合偏好  的大小。將
的大小。將  所包含的梯形模糊數(shù)轉(zhuǎn)化為參數(shù)化形式
所包含的梯形模糊數(shù)轉(zhuǎn)化為參數(shù)化形式  =(σ,x0,y0,β),其大小可依據(jù)式(3-14)計(jì)算:
=(σ,x0,y0,β),其大小可依據(jù)式(3-14)計(jì)算:
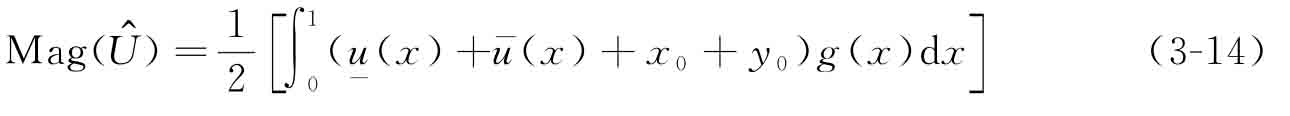
為方便計(jì)算,式(3-14)中加權(quán)函數(shù)取為g(x)=x。  的大小反映了其隸屬度的高低。
的大小反映了其隸屬度的高低。
步驟4 計(jì)算所有子目標(biāo)的權(quán)重系數(shù):

步驟5 利用式(3-16)給出的自適應(yīng)權(quán)重調(diào)整機(jī)制修正權(quán)重系數(shù):
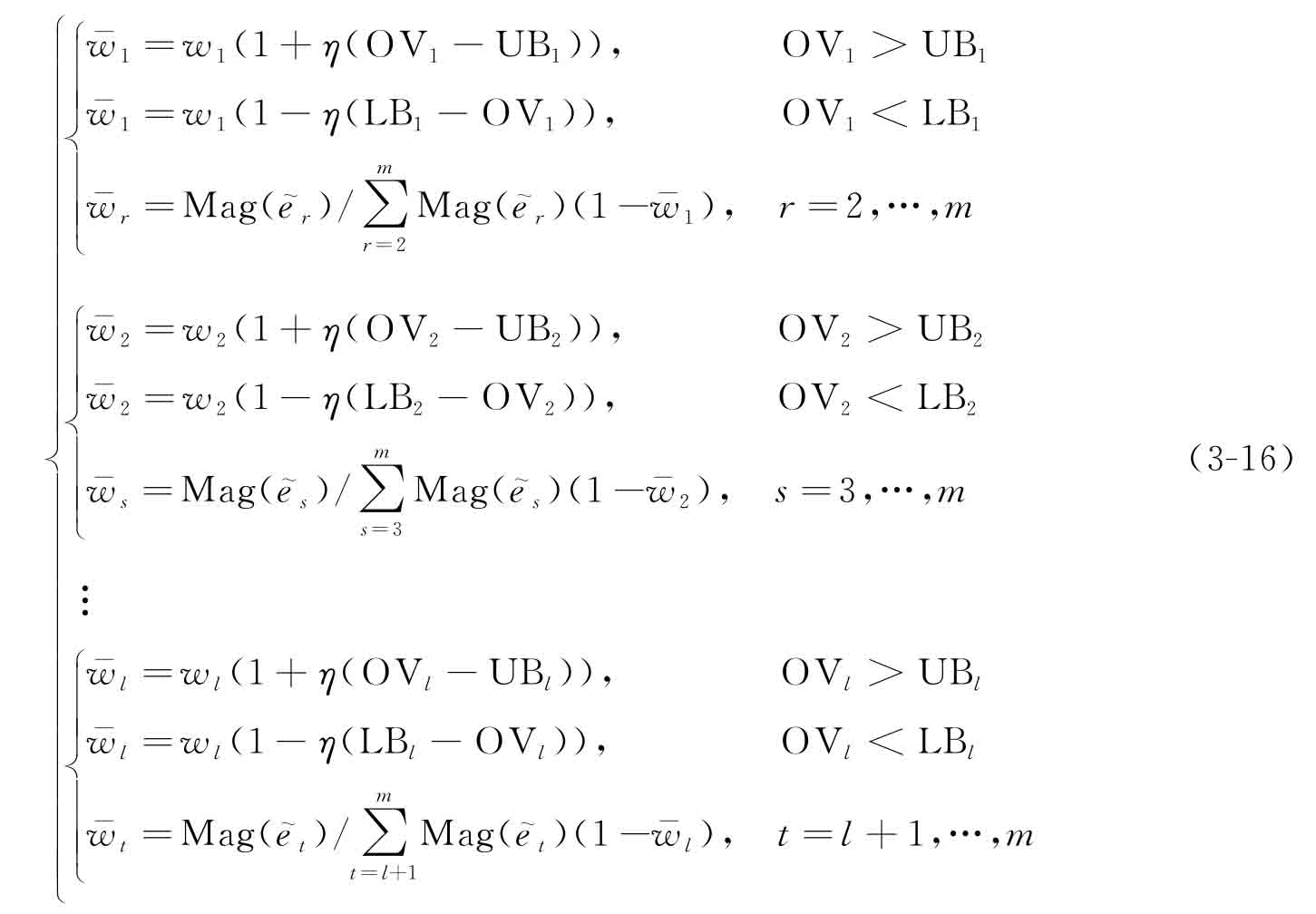
其中,OV代表子目標(biāo)函數(shù)值;UB和LB分別為子目標(biāo)取值的上限和下限;l代表需要修正權(quán)重系數(shù)的子目標(biāo)數(shù)量。較大的修正因子η會出現(xiàn)迭代不穩(wěn)定的問題,較小的η則會延長迭代收斂的時間,故在本章中取η=2。
所提出的權(quán)重計(jì)算方法具有非常鮮明的特點(diǎn):①采用語言術(shù)語描述是一種更加合理的方式,基于模糊集理論對語言術(shù)語進(jìn)行處理提高了所提出方法的實(shí)用性;②基于群決策的方式有效降低了權(quán)重計(jì)算錯誤的風(fēng)險,特殊的集結(jié)算子能夠過濾掉設(shè)計(jì)人員的極端偏好;③對于采用先決策后優(yōu)化方式的多目標(biāo)模型在應(yīng)用中更加便捷、簡單,且使用范圍廣。
3.1.4 靈敏度分析與優(yōu)化算法
與傳統(tǒng)拓?fù)鋬?yōu)化模型對比可以發(fā)現(xiàn),多目標(biāo)拓?fù)鋬?yōu)化設(shè)計(jì)模型式(3-9)中沒有任何結(jié)構(gòu)響應(yīng)約束,這表明無需在優(yōu)化求解過程中更新拉格朗日乘子。根據(jù)形狀導(dǎo)數(shù)概念分別對目標(biāo)函數(shù)中的結(jié)構(gòu)應(yīng)變能子目標(biāo)FC和體積子目標(biāo)FV進(jìn)行靈敏度分析,最后采用本書第2章所介紹的OC法對優(yōu)化模型進(jìn)行求解。
直接目標(biāo)函數(shù)FC對時間變量t的偏導(dǎo)可得
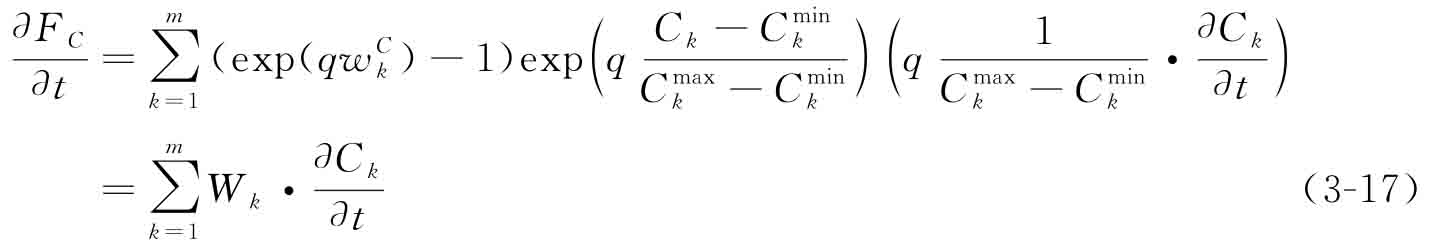
其中,偏導(dǎo)數(shù)?Ck/?t前的系數(shù)簡記為Wk。
結(jié)構(gòu)應(yīng)變能的形狀導(dǎo)數(shù)可推導(dǎo)為
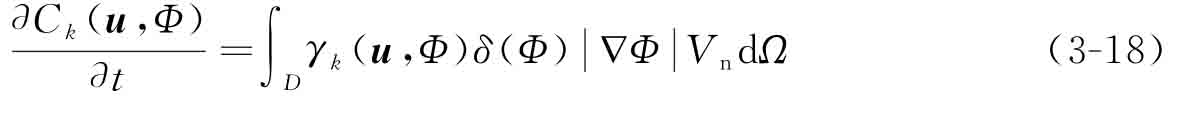
其中:
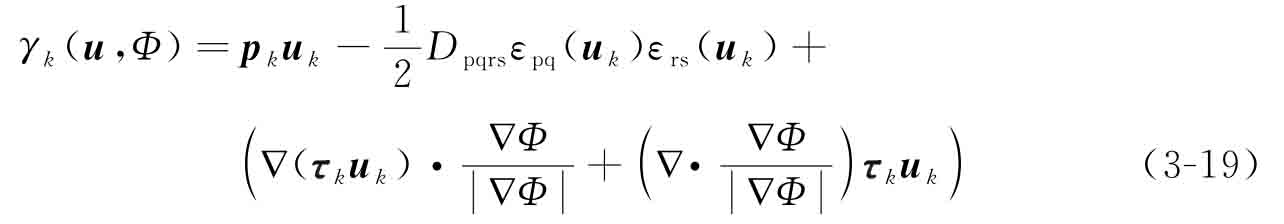
將式(2-22)定義的參數(shù)化水平集速度場代入式(3-18):
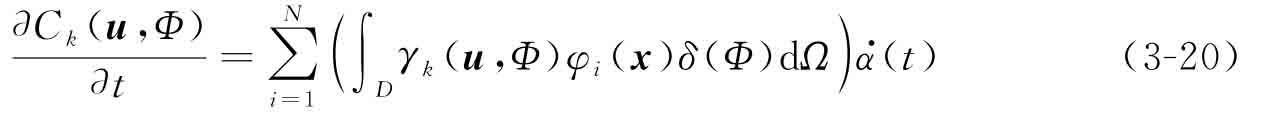
一方面,將式(3-20)代入式(3-17)可改寫目標(biāo)函數(shù)的形狀導(dǎo)數(shù):
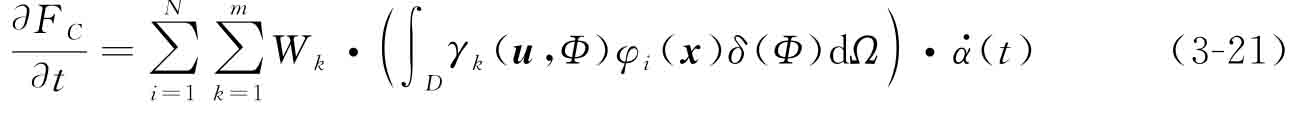
另一方面,采用鏈?zhǔn)角髮?dǎo)法則推導(dǎo)目標(biāo)函數(shù)FC關(guān)于時間變量t的偏導(dǎo):

對比式(3-21)和式(3-22),易知子目標(biāo)FC關(guān)于設(shè)計(jì)變量α的敏度為
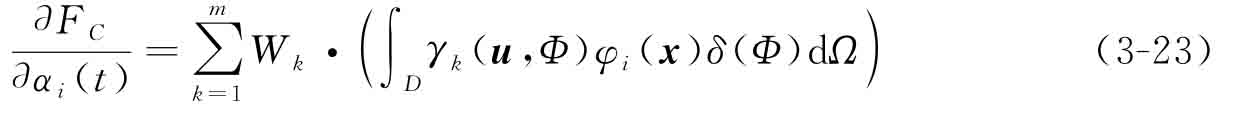
類似地,可推導(dǎo)體積子目標(biāo)FV關(guān)于設(shè)計(jì)變量α的敏度:
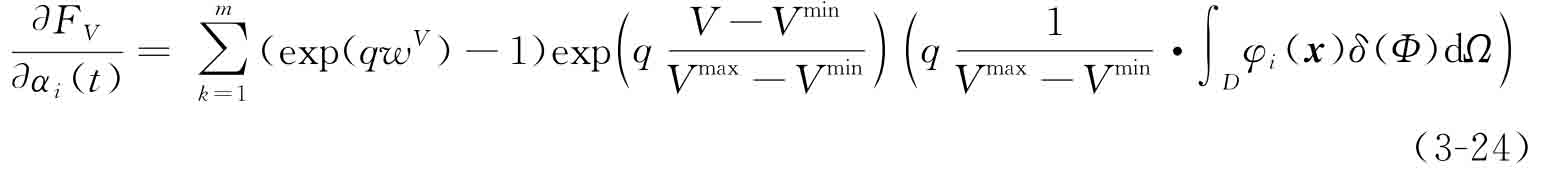
3.1.5 數(shù)值實(shí)例
1.二維懸臂結(jié)構(gòu)
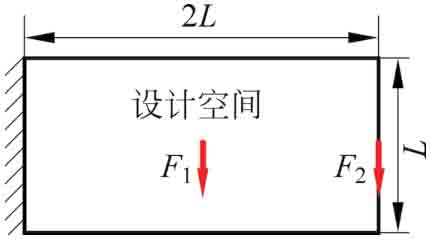
圖3-2 懸臂梁結(jié)構(gòu)的設(shè)計(jì)空間
平面懸臂梁的設(shè)計(jì)空間如圖3-2所示,長寬比為2∶1,左端固支,結(jié)構(gòu)域受2個載荷的作用,即F1=F2=500kN。材料的彈性模量為201GPa,泊松比為0.3。有限元單元與水平集網(wǎng)格離散均為120×60個。該優(yōu)化問題的目標(biāo)為同時優(yōu)化各子工況下的結(jié)構(gòu)柔度及體積分?jǐn)?shù)。
如前文所述,在加權(quán)多目標(biāo)優(yōu)化問題中,子目標(biāo)權(quán)重系數(shù)的大小對優(yōu)化設(shè)計(jì)結(jié)果有重要影響。為揭示權(quán)重系數(shù)大小與設(shè)計(jì)結(jié)果的內(nèi)在聯(lián)系,本例對不同權(quán)重系數(shù)下的多目標(biāo)拓?fù)鋬?yōu)化問題進(jìn)行了求解和對比分析。首先進(jìn)行11組試驗(yàn)(試驗(yàn)一),將結(jié)構(gòu)體積目標(biāo)的權(quán)重和各子工況下的柔度目標(biāo)權(quán)重和作為試驗(yàn)對象,采用試驗(yàn)設(shè)計(jì)(design of experiments,DOE)中的均分法,以0.1為試驗(yàn)間隔求解不同權(quán)重系數(shù)下的多目標(biāo)優(yōu)化問題。為方便討論,本例假設(shè)每個柔度子目標(biāo)的權(quán)重系數(shù)相等。理論上,體積目標(biāo)的權(quán)重與柔度目標(biāo)權(quán)重和的取值范圍為[0,1]。然而當(dāng)體積目標(biāo)的權(quán)重等于0時,結(jié)構(gòu)會刪除所有材料導(dǎo)致柔度無限大;當(dāng)柔度目標(biāo)權(quán)重和等于0時,結(jié)構(gòu)不會刪除任何材料導(dǎo)致優(yōu)化的結(jié)果為實(shí)體。這兩種情況在優(yōu)化中均無實(shí)際應(yīng)用價值,故將權(quán)重的變化范圍限定為[0.01,0.99]。
測試結(jié)果表明,當(dāng)體積目標(biāo)的權(quán)重系數(shù)大于一定值時,例如wV>0.3時,優(yōu)化迭代過程會隨著材料的急劇減少而不斷振蕩,從而直接導(dǎo)致優(yōu)化難以收斂(>400步迭代),優(yōu)化結(jié)果中某些結(jié)構(gòu)剛度路徑甚至?xí)驗(yàn)閮?yōu)化迭代過程振蕩發(fā)生斷裂。因此僅給出如表3-3和圖3-3所示的6組測試結(jié)果。為方便討論,在此定義一種材料性能指標(biāo)來反映最優(yōu)結(jié)構(gòu)拓?fù)渲忻恳粏挝粩?shù)量的材料減少所導(dǎo)致的結(jié)構(gòu)剛度喪失,即剛度降低率(decreasing ratio,DR):
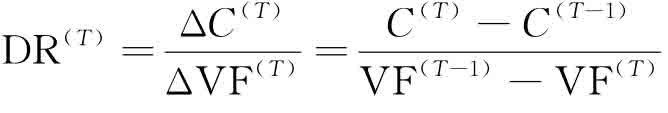
其中,ΔC和ΔVF分別代表相鄰兩次測試中結(jié)構(gòu)柔度的差值和體積分?jǐn)?shù)的差值;T代表不同試驗(yàn)的編號。DR的理論意義與經(jīng)濟(jì)學(xué)中的“邊際效益”類似,在此可稱之為“邊際剛度”(marginal stiffness):較大的DR意味著每減小一單位的結(jié)構(gòu)體積會導(dǎo)致結(jié)構(gòu)剛度的劇烈下降,此時以犧牲結(jié)構(gòu)剛度為代價來降低結(jié)構(gòu)重量是“不經(jīng)濟(jì)”的,反之亦然。
表3-3 試驗(yàn)一的數(shù)值結(jié)果比較
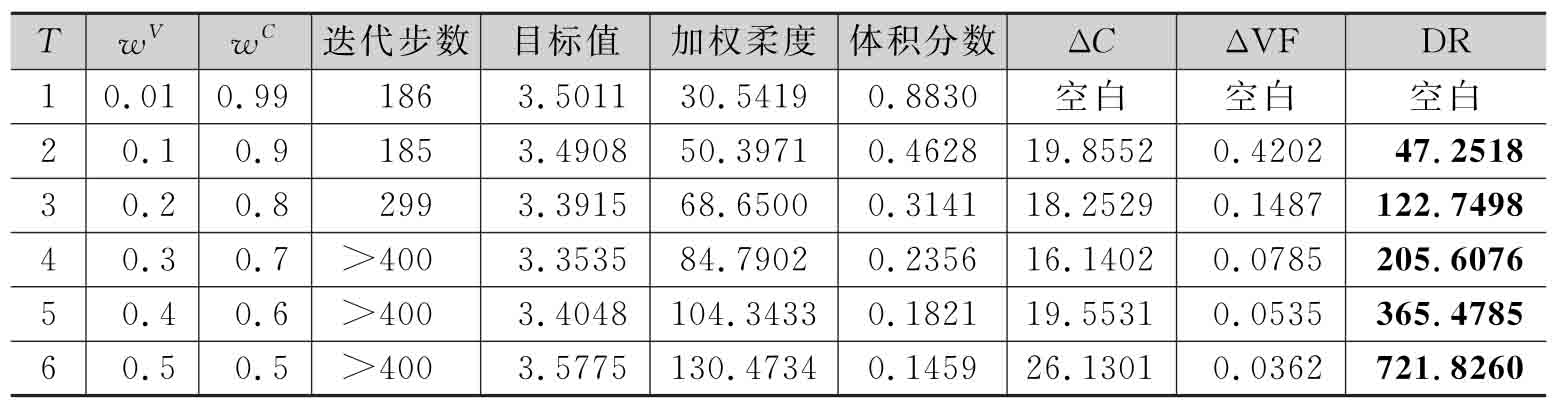
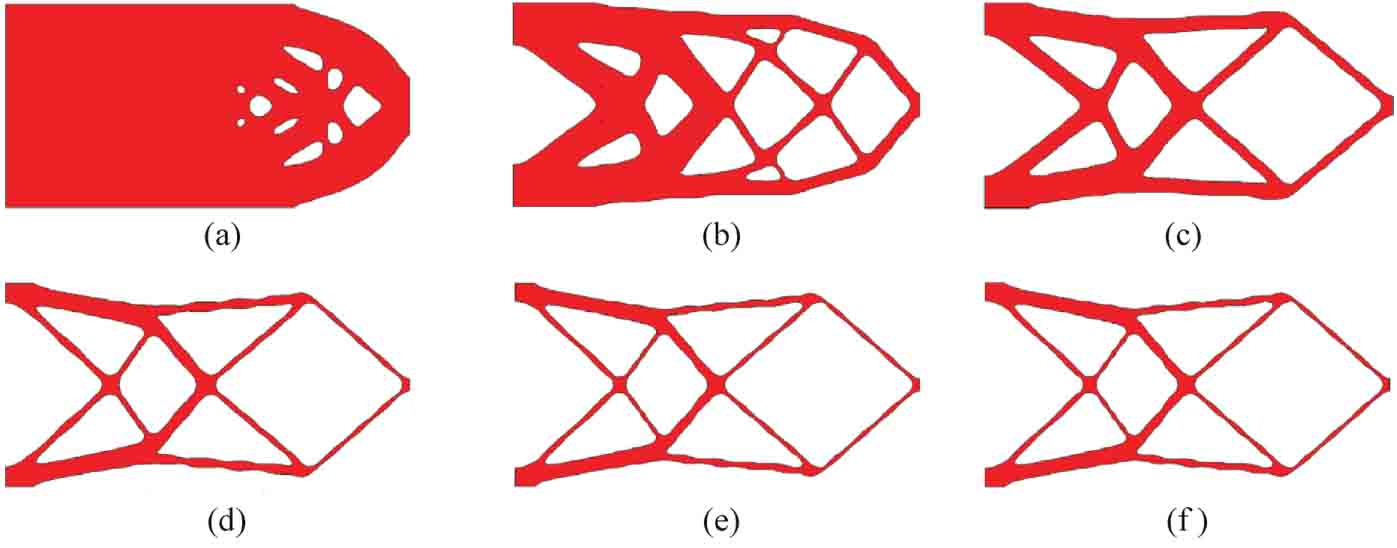
圖3-3 試驗(yàn)一的最優(yōu)結(jié)構(gòu)拓?fù)?/p>
(a)wV=0.01,wC=0.99;(b)wV=0.1,wC=0.9;(c)wV=0.2,wC=0.8;(d)wV=0.3,wC=0.7;(e)wV=0.4,wC=0.6;(f)wV=0.5,wC=0.5
從表3-3可以看到,當(dāng)結(jié)構(gòu)的最優(yōu)體積分?jǐn)?shù)在0.2以下時,DR值急劇增加,表明結(jié)構(gòu)的最優(yōu)剛度會隨著體積分?jǐn)?shù)的減小而劇烈下降。因此在二維情況下,推薦將考慮擴(kuò)展最優(yōu)性的多工況拓?fù)鋬?yōu)化問題的體積分?jǐn)?shù)下限設(shè)為0.2,以保證優(yōu)化結(jié)果材料使用的“經(jīng)濟(jì)性”。需要特別提出的是,三維空間的結(jié)構(gòu)拓?fù)鋬?yōu)化問題不同于二維問題。測試結(jié)果表明,由于三維結(jié)構(gòu)具有更強(qiáng)的承載能力,體積分?jǐn)?shù)下限可設(shè)置為0.1。從圖3-3可以看出,不同權(quán)重系數(shù)的組合會得到不同拓?fù)湫问降膬?yōu)化結(jié)果,但本方法始終能保證結(jié)構(gòu)邊界的清晰和光滑。
此外,數(shù)值算例表明當(dāng)體積目標(biāo)的權(quán)重系數(shù)在[0.01,0.99]間取值時,最優(yōu)設(shè)計(jì)的拓?fù)錁?gòu)型對權(quán)重系數(shù)十分敏感。表3-4和圖3-4分別給出了試驗(yàn)二的數(shù)值結(jié)果和結(jié)構(gòu)拓?fù)湫问健?yōu)化結(jié)果顯示,體積目標(biāo)的權(quán)重系數(shù)的微小改變就會導(dǎo)致優(yōu)化設(shè)計(jì)的體積分?jǐn)?shù)發(fā)生較大差異,尤其是當(dāng)權(quán)重系數(shù)wV<0.05時最優(yōu)設(shè)計(jì)的體積分?jǐn)?shù)變化更加明顯。通過控制體積分?jǐn)?shù)上限可一定程度避免權(quán)重系數(shù)的微小改變帶來體積分?jǐn)?shù)的劇烈波動。而且為實(shí)現(xiàn)結(jié)構(gòu)的輕量化設(shè)計(jì),工程上通常將優(yōu)化設(shè)計(jì)方案的體積分?jǐn)?shù)設(shè)置在0.5附近。在本實(shí)例中體積分?jǐn)?shù)0.5將被設(shè)置為體積目標(biāo)值的上限,以保證優(yōu)化結(jié)果的減重效果。
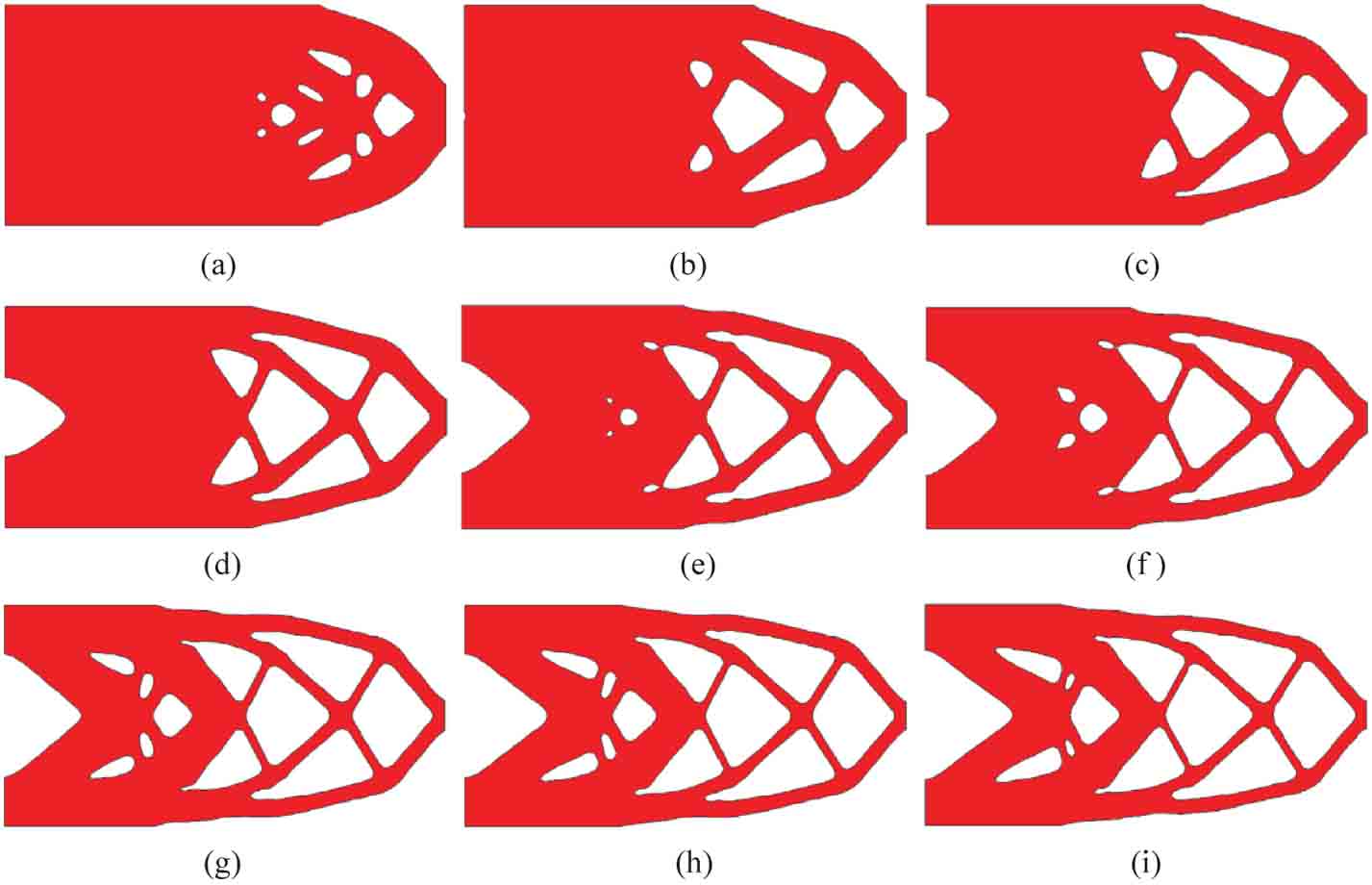
圖3-4 試驗(yàn)二的最優(yōu)結(jié)構(gòu)拓?fù)?/p>
(a)wV=0.01,wC=0.99;(b)wV=0.02,wC=0.98;(c)wV=0.03,wC=0.97;(d)wV=0.04,wC=0.96;(e)wV=0.05,wC=0.95;(f)wV=0.06,wC=0.94;(g)wV=0.07,wC=0.93;(h)wV=0.08,wC=0.92;(i)wV=0.09,wC=0.91
表3-4 試驗(yàn)二的數(shù)值結(jié)果比較
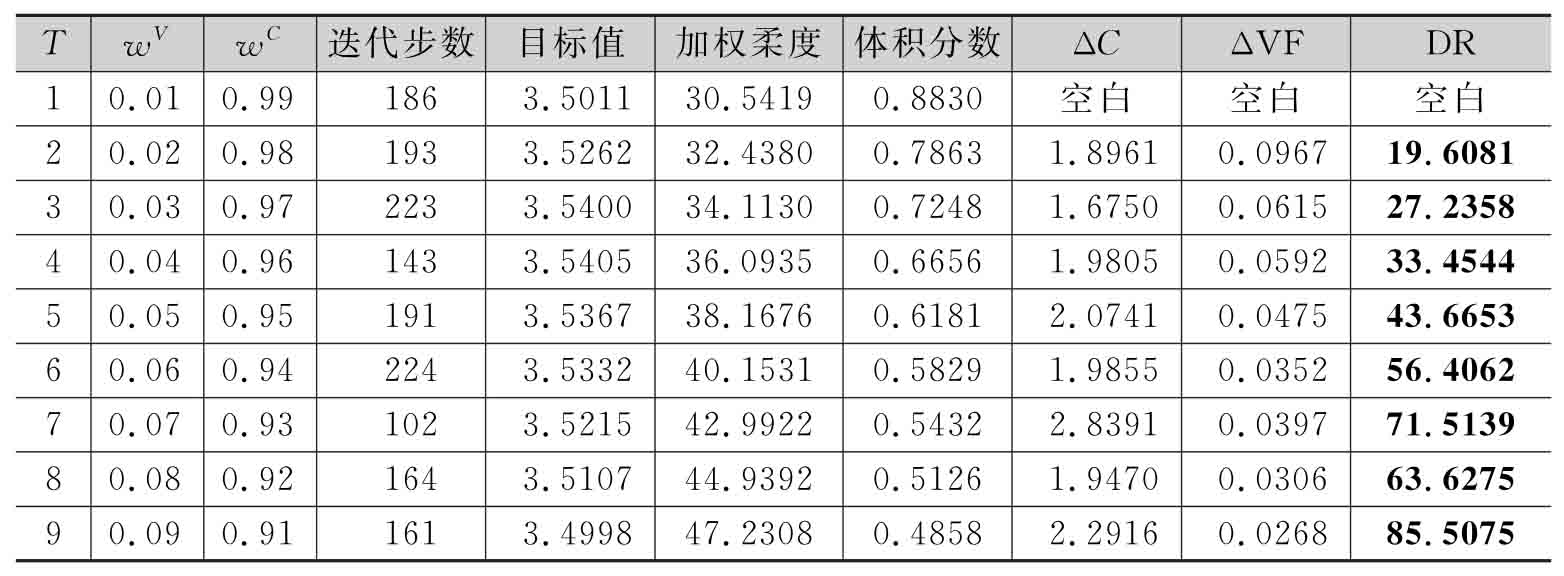
將各工況下結(jié)構(gòu)柔度的加權(quán)和作為一種特殊的結(jié)構(gòu)柔度目標(biāo),結(jié)構(gòu)的體積分?jǐn)?shù)作為體積目標(biāo),可將考慮擴(kuò)展最優(yōu)性的拓?fù)鋬?yōu)化問題簡化視為一種兩目標(biāo)優(yōu)化問題。經(jīng)簡化后的優(yōu)化問題的部分Pareto最優(yōu)前端如圖3-5所示。
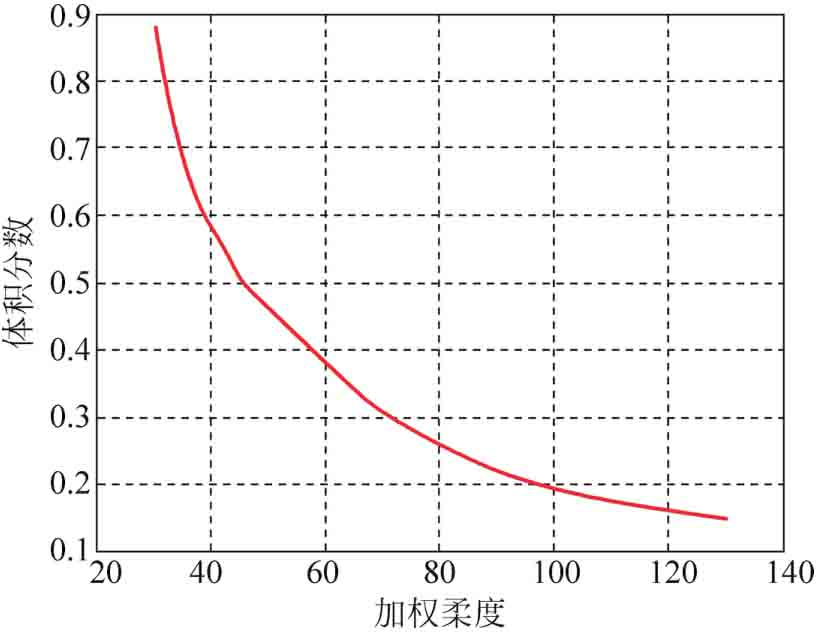
圖3-5 簡化為兩目標(biāo)優(yōu)化問題時的部分Pareto最優(yōu)前端
2.二維橋梁結(jié)構(gòu)
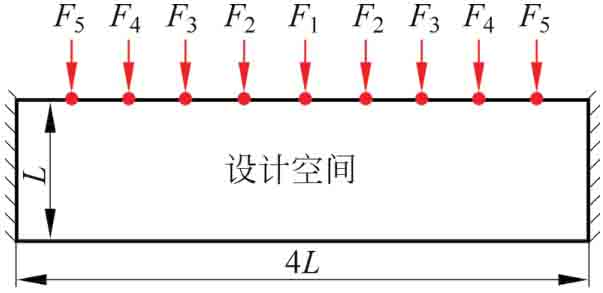
圖3-6 橋梁結(jié)構(gòu)的設(shè)計(jì)空間
橋梁的拓?fù)鋬?yōu)化屬于大型連續(xù)稀疏結(jié)構(gòu)的設(shè)計(jì)問題,在實(shí)際工程中該問題會涉及十分復(fù)雜的工況載荷。橋梁結(jié)構(gòu)的設(shè)計(jì)空間如圖3-6所示,橋面以下左右端固支,橋面上綜合作用5種載荷工況,且F1=F2=F3=F4=F5=50kN。材料的彈性模量為180GPa,泊松比為0.3。整個結(jié)構(gòu)設(shè)計(jì)域采用240×60個四邊形單元進(jìn)行離散,其中橋面(受載區(qū)域)為非設(shè)計(jì)區(qū)域,由240×2個被動單元(passive element)構(gòu)成,與被動單元關(guān)聯(lián)的CSRBF擴(kuò)展系數(shù)不參與優(yōu)化迭代。該優(yōu)化問題的目標(biāo)為同時最小化各子工況下的結(jié)構(gòu)柔度及體積分?jǐn)?shù)。利用結(jié)構(gòu)對稱性,僅7200個單元參與計(jì)算。
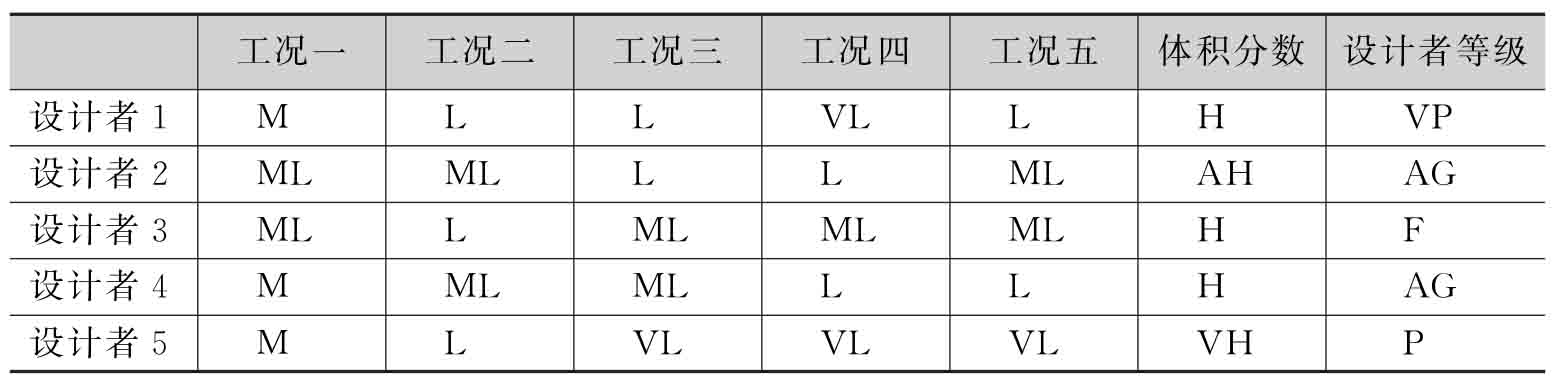
首先采用基于FMAGDM的權(quán)重計(jì)算方法確定多目標(biāo)拓?fù)鋬?yōu)化問題的權(quán)重。5個設(shè)計(jì)者對6個目標(biāo)的評價,以及5位設(shè)計(jì)者的水平及經(jīng)驗(yàn)的綜合等級如表3-5所示。為說明方法的穩(wěn)定性,特別令設(shè)計(jì)者1給出與其他設(shè)計(jì)者完全相反的極端評價意見。通過計(jì)算,可以快速得到規(guī)范化的子目標(biāo)權(quán)重系數(shù)w=[0.2356,0.1514,0.0982,0.0952,0.0911,0.3285]。計(jì)算結(jié)果表明,個別極端的評價意見對最終的權(quán)重系數(shù)確定沒有明顯影響。
表3-5 5位設(shè)計(jì)者的第一種偏好
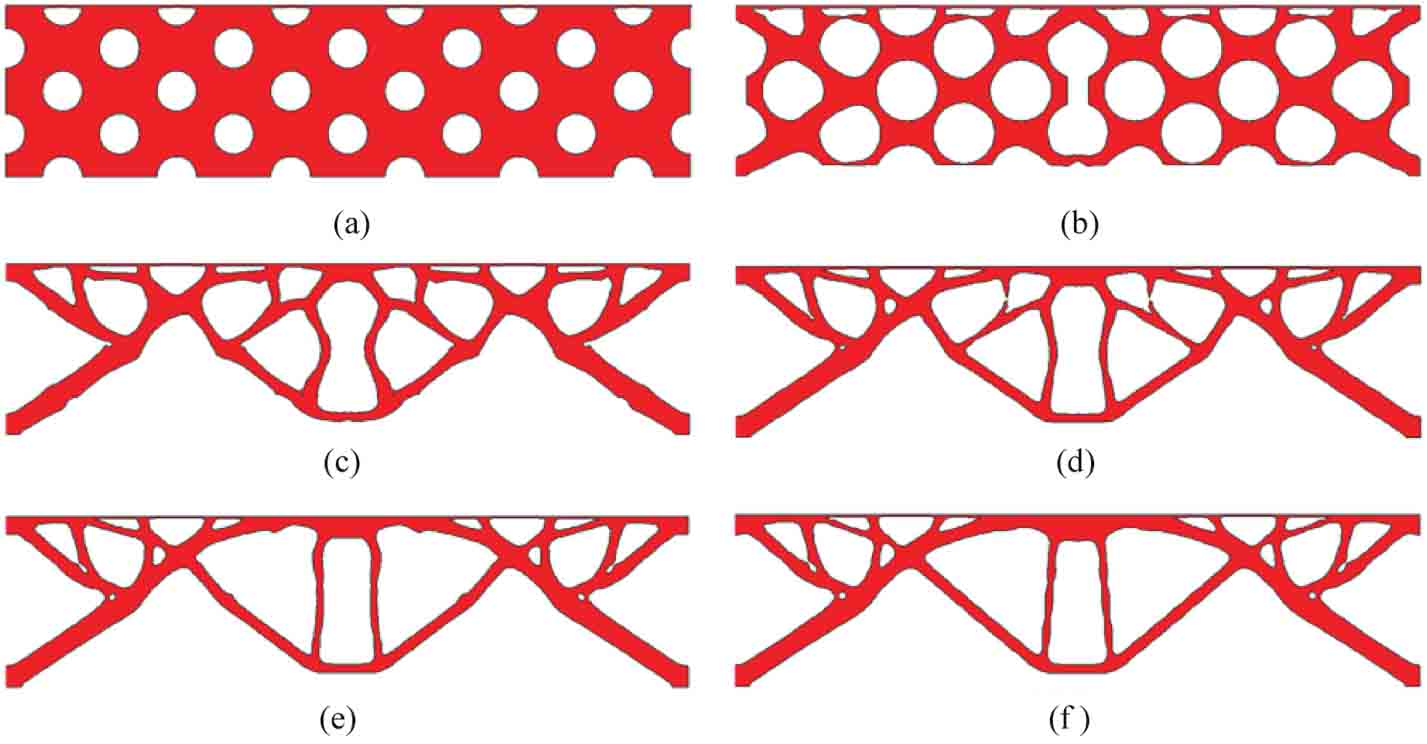
圖3-7 結(jié)構(gòu)邊界的優(yōu)化過程
(a)初始設(shè)計(jì);(b)第5步迭代;(c)第10步迭代;(d)第20步迭代;(e)第40步迭代;(f)最終設(shè)計(jì)
接著對基于NEWC的多目標(biāo)優(yōu)化模型進(jìn)行求解。通過對各工況單獨(dú)作用時拓?fù)鋬?yōu)化問題的快速求解,可以預(yù)估子目標(biāo)的最大和最小值:  =25.8242和
=25.8242和  =0.2584;
=0.2584;  =18.8834和
=18.8834和  =0.1881;
=0.1881;  =13.5942和
=13.5942和  =0.1356;
=0.1356;  =8.7989和
=8.7989和  =0.0879;
=0.0879;  =5.4642和
=5.4642和  =0.0549。經(jīng)過優(yōu)化迭代,本問題的最優(yōu)目標(biāo)函數(shù)值為3.1235,其對應(yīng)的各子工況下的最優(yōu)結(jié)構(gòu)柔度值為C=[1.3292,0.9653,0.5900,0.3686,0.3038],結(jié)構(gòu)體積分?jǐn)?shù)為0.2479,迭代步數(shù)為151,對應(yīng)的結(jié)構(gòu)最優(yōu)拓?fù)湫问饺鐖D3-7(f)。結(jié)構(gòu)拓?fù)洹⑺郊瘮?shù)及CSRBF擴(kuò)展系數(shù)分布的演化過程分別如圖3-7、圖3-8和圖3-9所示。可以看到結(jié)構(gòu)邊界在優(yōu)化初期經(jīng)歷劇烈的拓?fù)浜托螤钭兓罱K收斂到光滑的最優(yōu)拓?fù)湫螤睿f明該方法很好地保留了水平集方法的優(yōu)點(diǎn)。擴(kuò)展系數(shù)作為設(shè)計(jì)變量在優(yōu)化過程中動態(tài)地調(diào)整,優(yōu)化后的擴(kuò)展系數(shù)沿結(jié)構(gòu)邊界均勻化分布,表明優(yōu)化過程已趨于穩(wěn)定,此時的結(jié)構(gòu)邊界Γd應(yīng)為最優(yōu)邊界
=0.0549。經(jīng)過優(yōu)化迭代,本問題的最優(yōu)目標(biāo)函數(shù)值為3.1235,其對應(yīng)的各子工況下的最優(yōu)結(jié)構(gòu)柔度值為C=[1.3292,0.9653,0.5900,0.3686,0.3038],結(jié)構(gòu)體積分?jǐn)?shù)為0.2479,迭代步數(shù)為151,對應(yīng)的結(jié)構(gòu)最優(yōu)拓?fù)湫问饺鐖D3-7(f)。結(jié)構(gòu)拓?fù)洹⑺郊瘮?shù)及CSRBF擴(kuò)展系數(shù)分布的演化過程分別如圖3-7、圖3-8和圖3-9所示。可以看到結(jié)構(gòu)邊界在優(yōu)化初期經(jīng)歷劇烈的拓?fù)浜托螤钭兓罱K收斂到光滑的最優(yōu)拓?fù)湫螤睿f明該方法很好地保留了水平集方法的優(yōu)點(diǎn)。擴(kuò)展系數(shù)作為設(shè)計(jì)變量在優(yōu)化過程中動態(tài)地調(diào)整,優(yōu)化后的擴(kuò)展系數(shù)沿結(jié)構(gòu)邊界均勻化分布,表明優(yōu)化過程已趨于穩(wěn)定,此時的結(jié)構(gòu)邊界Γd應(yīng)為最優(yōu)邊界  。從優(yōu)化后的結(jié)構(gòu)拓?fù)鋪砜矗我还r載荷作用處均有相應(yīng)的剛度傳遞路徑延伸出來,并最終與主傳遞路徑交匯,保證了剛度的有效傳遞,說明本節(jié)所涉及的方法可以有效地克服多工況拓?fù)鋬?yōu)化問題中載荷病態(tài)的缺陷。
。從優(yōu)化后的結(jié)構(gòu)拓?fù)鋪砜矗我还r載荷作用處均有相應(yīng)的剛度傳遞路徑延伸出來,并最終與主傳遞路徑交匯,保證了剛度的有效傳遞,說明本節(jié)所涉及的方法可以有效地克服多工況拓?fù)鋬?yōu)化問題中載荷病態(tài)的缺陷。
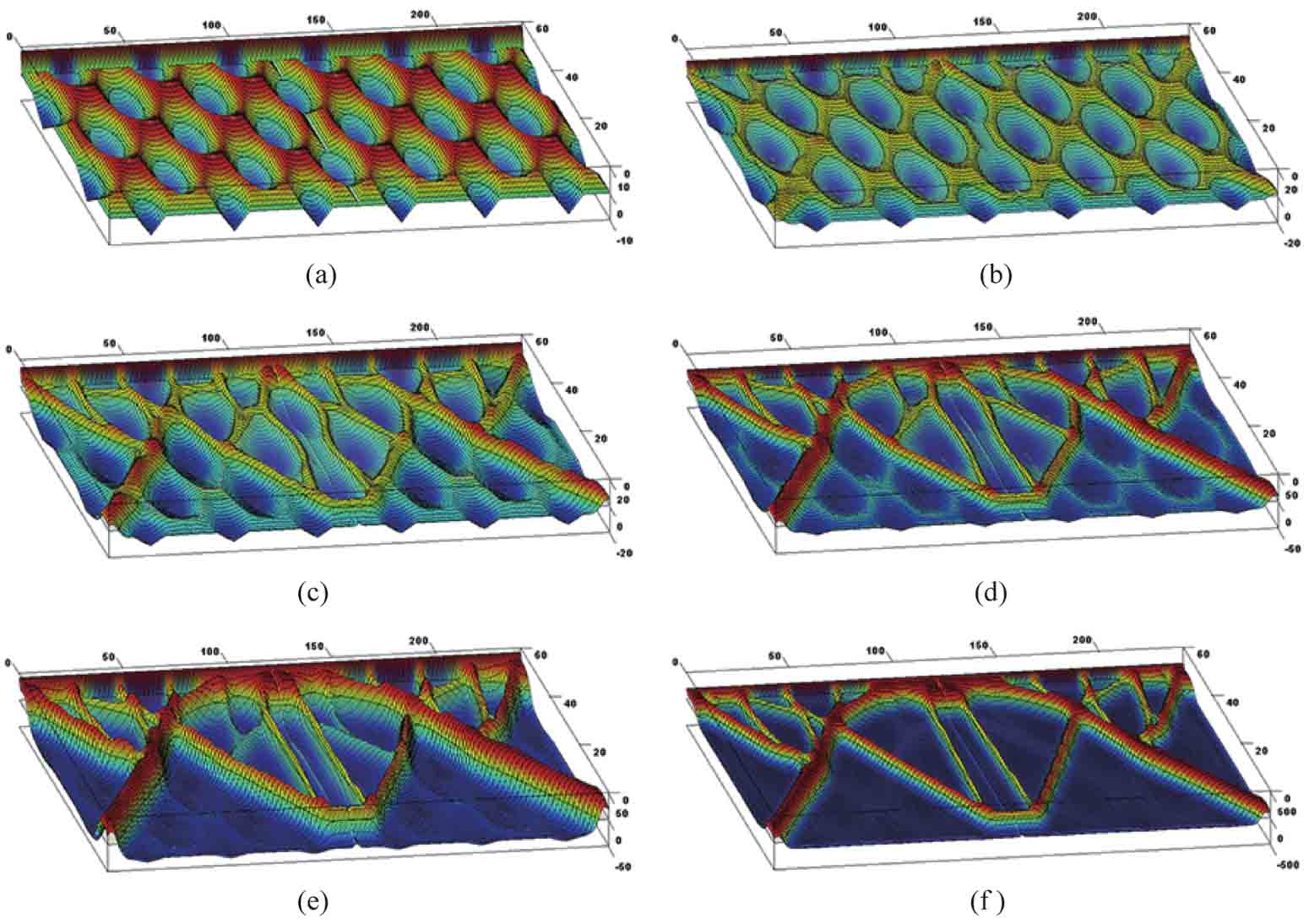
圖3-8 水平集面的演化過程
(a)初始設(shè)計(jì);(b)第5步迭代;(c)第10步迭代;(d)第20步迭代;(e)第40步迭代;(f)最終設(shè)計(jì)
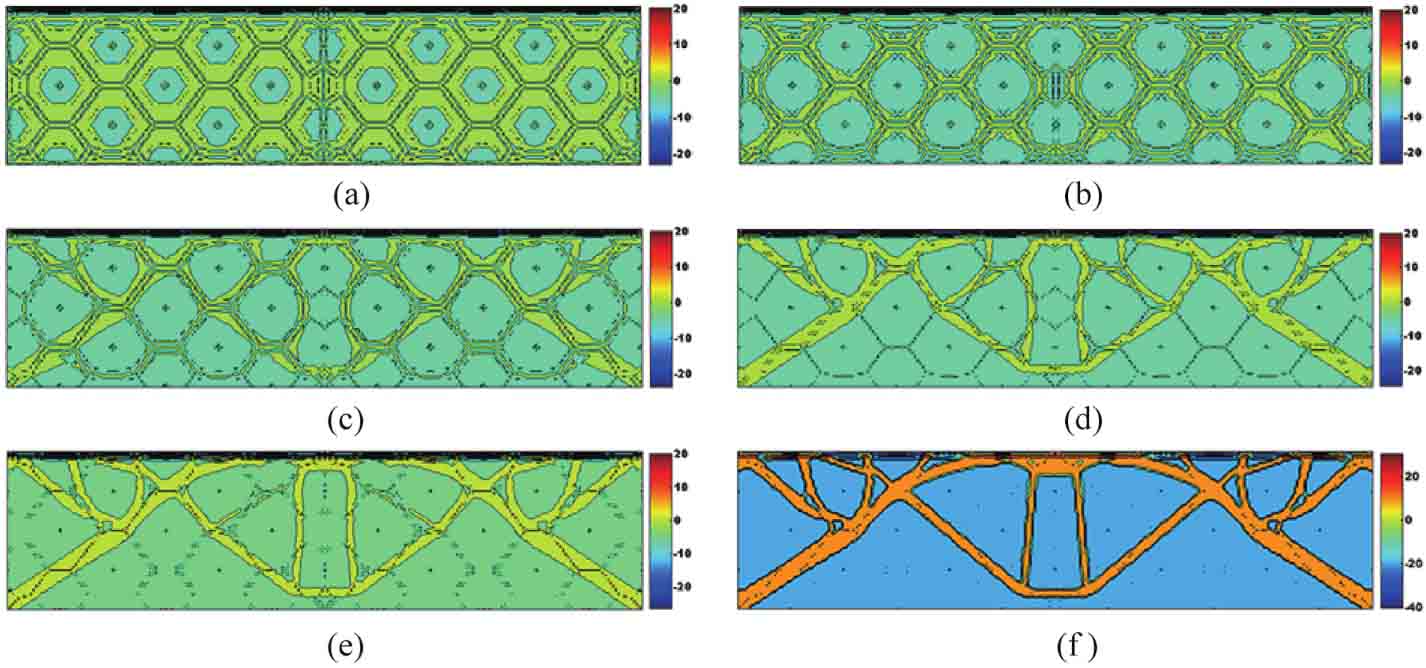
圖3-9 擴(kuò)展系數(shù)分布的變化過程
(a)初始設(shè)計(jì);(b)第5步迭代;(c)第10步迭代;(d)第20步迭代;(e)第40步迭代;(f)最終設(shè)計(jì)
優(yōu)化問題的迭代收斂曲線如圖3-10所示。各子目標(biāo)的收斂曲線如圖3-11所示。從圖3-10中看到,整個優(yōu)化迭代過程高效且穩(wěn)定,目標(biāo)函數(shù)值在第20步迭代時已逼近最優(yōu)值,此時結(jié)構(gòu)的拓?fù)浠拘纬桑w積約束已接近設(shè)定的體積分?jǐn)?shù),后續(xù)131步迭代過程主要是針對結(jié)構(gòu)局部拓?fù)涞奈⒄{(diào)以及進(jìn)行結(jié)構(gòu)形狀優(yōu)化。從圖3-11可以看到,在初始的20步迭代內(nèi),各子目標(biāo)值均發(fā)生了一定程度的變化,部分目標(biāo)值甚至出現(xiàn)局部振蕩,主要是因?yàn)榈跗诮Y(jié)構(gòu)的材料去除速度較快,導(dǎo)致拓?fù)渥兓^大,各子目標(biāo)通過不斷變化以便獲得較為穩(wěn)定的折中值。在這一迭代階段完成后,各子目標(biāo)值均開始穩(wěn)定收斂,最終得到相應(yīng)的Pareto最優(yōu)解。說明該方法對二維拓?fù)鋬?yōu)化設(shè)計(jì)問題的有效性。
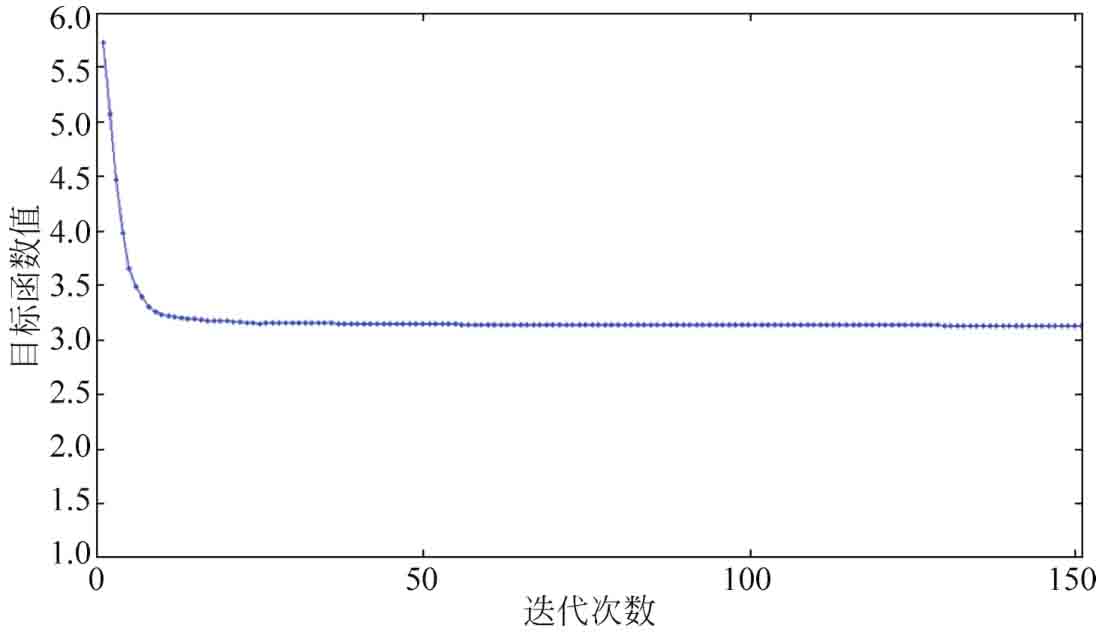
圖3-10 多目標(biāo)優(yōu)化問題的收斂曲線
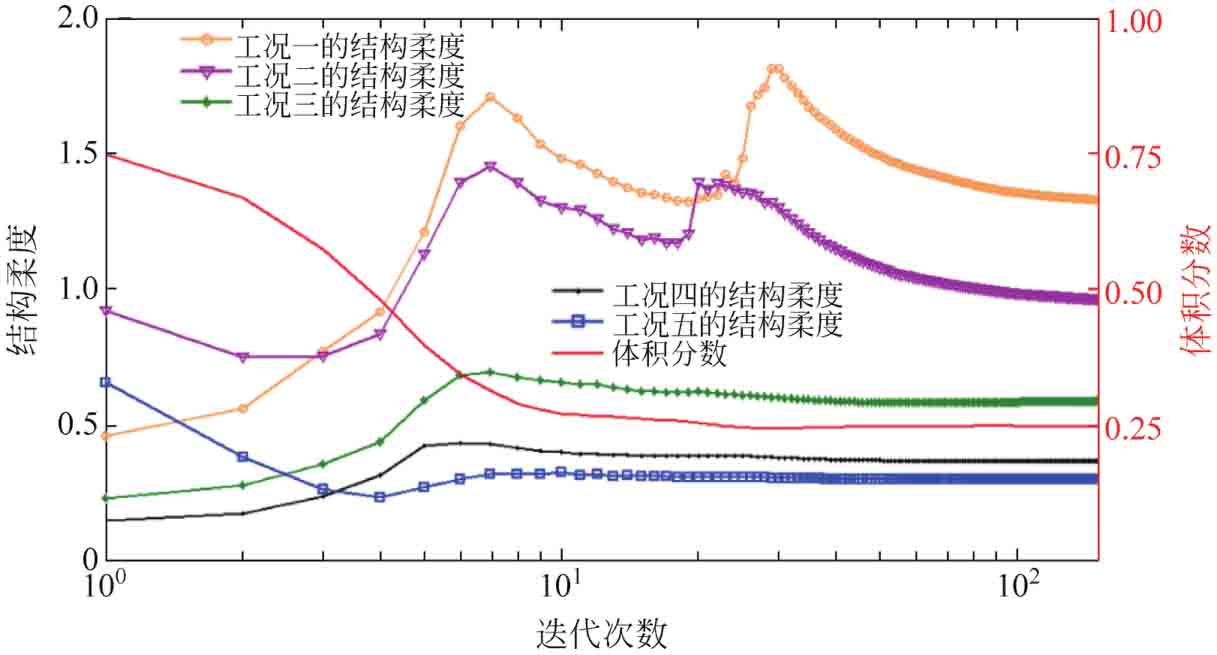
圖3-11 各子目標(biāo)的收斂曲線
考慮到拓?fù)鋬?yōu)化中存在的“邊際剛度”隨體積分?jǐn)?shù)的減少而快速遞減的現(xiàn)象,最優(yōu)設(shè)計(jì)的體積分?jǐn)?shù)會直接影響材料的使用效率以及結(jié)構(gòu)的性能。在考慮擴(kuò)展最優(yōu)性的拓?fù)鋬?yōu)化問題中,結(jié)構(gòu)的體積分?jǐn)?shù)在優(yōu)化前是未知的,當(dāng)設(shè)計(jì)者對體積目標(biāo)給出較為過大或過小的權(quán)重系數(shù)時,結(jié)構(gòu)的體積分?jǐn)?shù)也會相應(yīng)地達(dá)到某種過高或過低的水平。因此引入自適應(yīng)權(quán)重調(diào)整機(jī)制將二維拓?fù)鋬?yōu)化問題的最優(yōu)體積分?jǐn)?shù)維持在區(qū)間[0.2,0.5]內(nèi),以保證材料使用的經(jīng)濟(jì)性。根據(jù)式(3-16)可得到關(guān)于體積目標(biāo)權(quán)重系數(shù)的自適應(yīng)調(diào)整算子,用于進(jìn)行體積目標(biāo)和柔度目標(biāo)權(quán)重系數(shù)的修正。
為說明自適應(yīng)權(quán)重調(diào)整機(jī)制的作用,本例給出另外5位設(shè)計(jì)者對6個子目標(biāo)的偏好矩陣,其中所有設(shè)計(jì)者均對體積目標(biāo)較為偏重,見表3-6。通過計(jì)算可獲得規(guī)范化的權(quán)重系數(shù)w=[0.1503,0.1036,0.0819,0.0702,0.0819,0.5121]。
表3-6 5位設(shè)計(jì)者的第二種偏好
設(shè)計(jì)者第二種偏好下的橋梁結(jié)構(gòu)最優(yōu)拓?fù)湫问饺鐖D3-12所示。結(jié)構(gòu)的體積分?jǐn)?shù)和體積目標(biāo)權(quán)重的收斂曲線如圖3-13所示。從圖中可知,前15次迭代中結(jié)構(gòu)的體積分?jǐn)?shù)總是高于所設(shè)定的下限值(圖中紅色虛線),此時的結(jié)構(gòu)體積分?jǐn)?shù)穩(wěn)定下降,體積目標(biāo)權(quán)重值保持不變,材料使用的“經(jīng)濟(jì)性”良好。從第16次迭代開始,體積分?jǐn)?shù)開始低于下限值0.2,材料的使用變?yōu)椤安唤?jīng)濟(jì)”的狀態(tài),自適應(yīng)權(quán)重調(diào)整機(jī)制開始起作用,體積目標(biāo)權(quán)重開始逐漸下降,直到第54次迭代結(jié)構(gòu)的體積分?jǐn)?shù)被拉升到下限值以上,此時體積目標(biāo)權(quán)重維持不變。各子工況下的最優(yōu)柔度值為2.0338、1.4036、0.6774、0.5646和0.4039,體積分?jǐn)?shù)為0.2006,迭代步數(shù)為232。特別指出,雖然結(jié)構(gòu)初始化的體積分?jǐn)?shù)可能高于上限值0.5,但隨著OC算法的迭代,體積分?jǐn)?shù)值會迅速下降至上限值以下,故可以假設(shè)在這一階段上限值是不起作用的。本實(shí)例說明所論述的優(yōu)化方法能通過調(diào)整權(quán)重值來保證材料的使用效率。

圖3-12 設(shè)計(jì)者第二種偏好下的最優(yōu)結(jié)構(gòu)拓?fù)?/p>
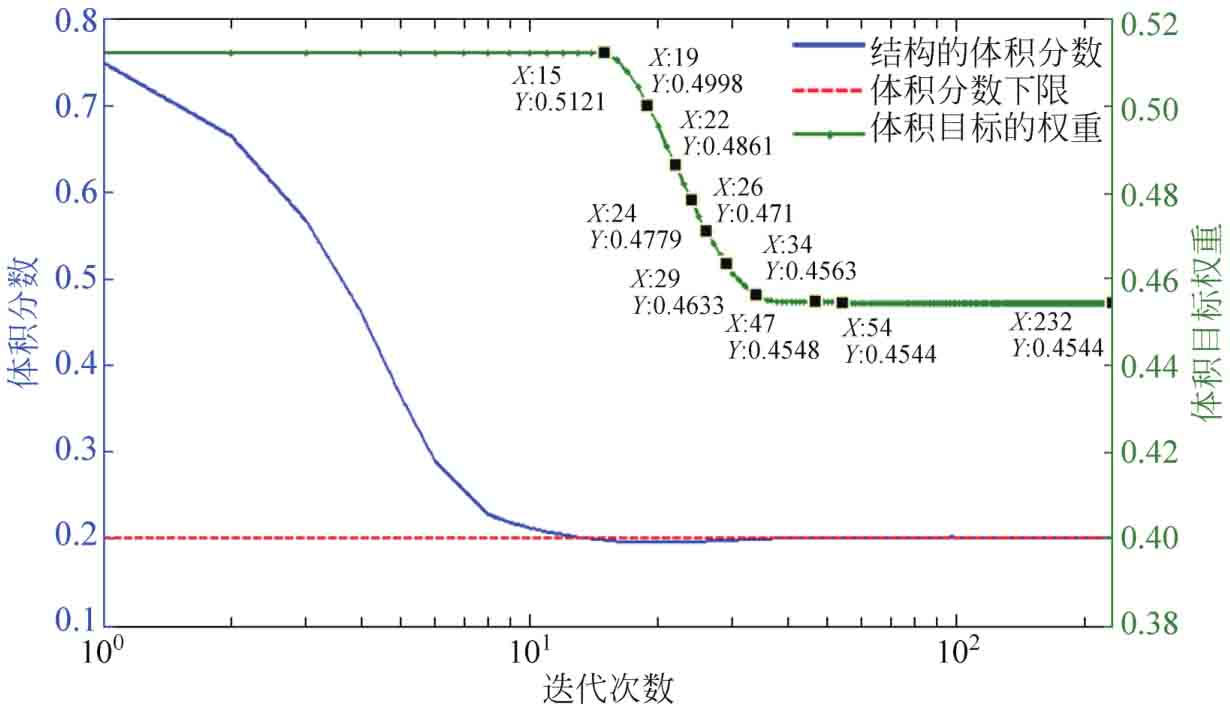
圖3-13 體積子目標(biāo)的收斂曲線
- 數(shù)據(jù)庫系統(tǒng)原理及MySQL應(yīng)用教程(第2版)
- UML和模式應(yīng)用(原書第3版)
- C# 2012程序設(shè)計(jì)實(shí)踐教程 (清華電腦學(xué)堂)
- Visual Basic 6.0程序設(shè)計(jì)計(jì)算機(jī)組裝與維修
- R語言數(shù)據(jù)可視化實(shí)戰(zhàn)
- Processing互動編程藝術(shù)
- 教孩子學(xué)編程:C++入門圖解
- The DevOps 2.4 Toolkit
- Mastering Apache Spark 2.x(Second Edition)
- 常用工具軟件立體化教程(微課版)
- App Inventor創(chuàng)意趣味編程進(jìn)階
- Beginning C++ Game Programming
- 從Excel到Python數(shù)據(jù)分析:Pandas、xlwings、openpyxl、Matplotlib的交互與應(yīng)用
- Redmine Cookbook
- Tkinter GUI Programming by Example