- 胸有成竹!數(shù)據(jù)分析的SPSS和SAS EG進階(第2版)
- 經(jīng)管之家主編 常國珍等編著
- 5039字
- 2021-10-29 11:58:03
2.2 單變量描述統(tǒng)計方法
對于單變量的描述有兩類方法,一類是統(tǒng)計量,另一類是圖形。前者信息量較大,后者更直觀。以下按分類變量和連續(xù)變量,分別介紹不同的描述性統(tǒng)計方法。
2.2.1 分類變量的描述
對于分類變量,主要的統(tǒng)計量有以下幾個。
● 頻次:每個水平出現(xiàn)的次數(shù);
● 百分比:每個水平出現(xiàn)的頻數(shù)除以總數(shù);
● 累積頻次:僅對于等級變量有意義,為截止到當(dāng)前水平的累積頻次;
● 累積百分比:僅對于等級變量有意義,為截止到當(dāng)前水平的累積百分比。
對于名義變量,只有頻次和百分比有意義。等級變量不但頻次和百分比有意義,累積頻次和累積百分比也有意義。如圖2-2所示,“PROFIT”數(shù)據(jù)中不同訂單類型的頻次。由于訂單類型是名義變量,只有頻數(shù)和百分比具有意義。
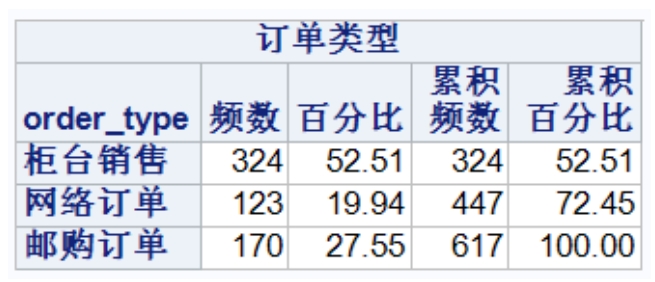
圖2-2
同樣的信息可以使用柱形圖來表示,如圖2-3所示。其坐標(biāo)軸表示不同的水平,柱高頻數(shù)或百分比。
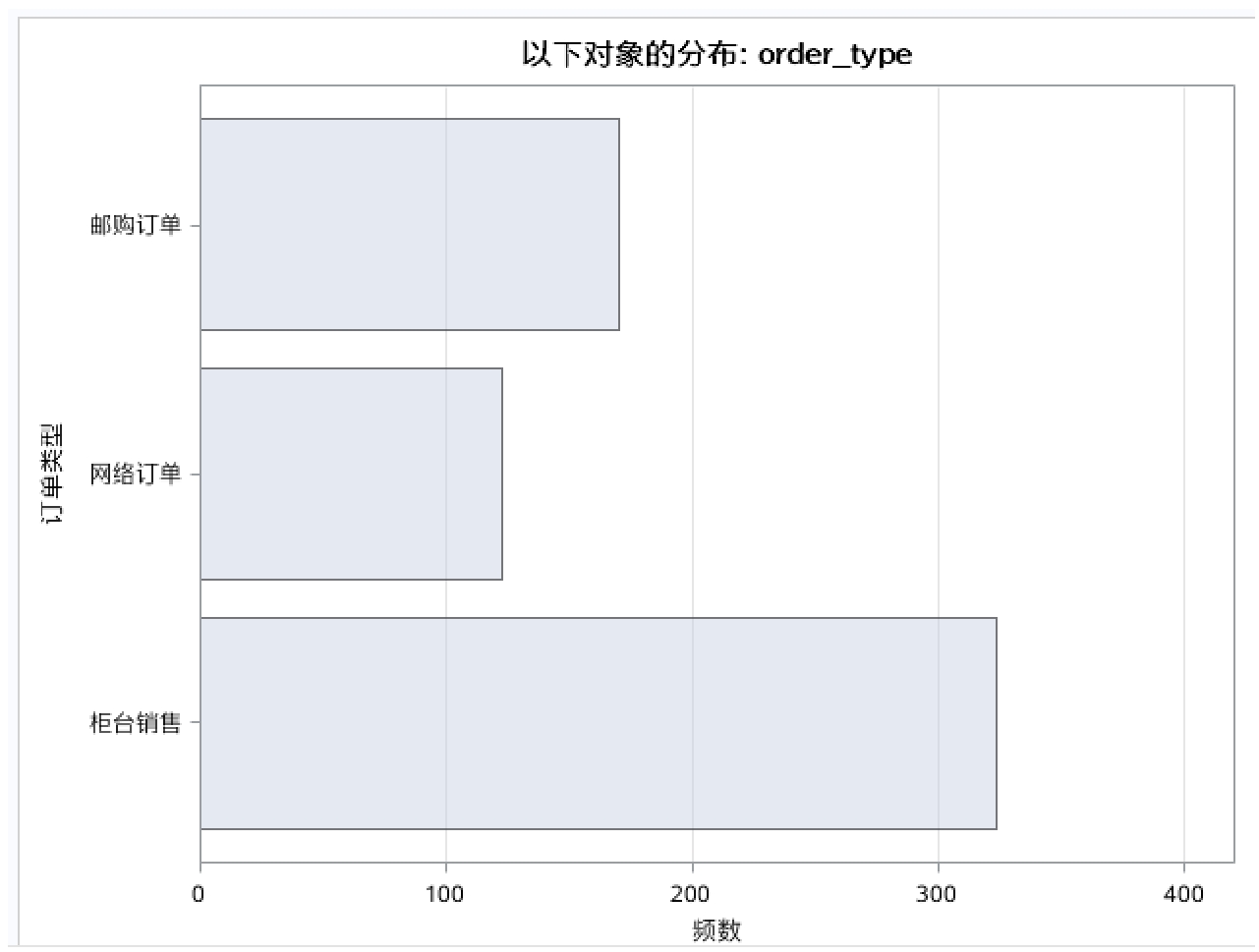
圖2-3
2.2.2 連續(xù)變量的描述
連續(xù)變量的描述強調(diào)對變量進行分布探索,包括中心水平、離散程度、偏態(tài)程度和峰度4個方面。有人會問為什么要對連續(xù)變量計算這4類指標(biāo),這些指標(biāo)有什么意義?是否夠全面?假設(shè)自己是一名國家統(tǒng)計局的員工,領(lǐng)導(dǎo)詢問我們今年上海和廣州的居民收入情況,請考慮一下該如何回答?
 統(tǒng)計量
統(tǒng)計量
(1)中心水平
在遇到一個變量的時候,最先想到的是如何找到一個指標(biāo)可以表達這個變量的水平,一般我們習(xí)慣拿“中心”來代表。能代表“中心”概念的可選統(tǒng)計量有均值(總合與均值的概念相似)、中位數(shù)和眾數(shù),如圖2-4所示。其中均值的計算公式雖然最復(fù)雜,但是它是參數(shù)估計的基礎(chǔ),后續(xù)會接觸到參數(shù)方法中所有的預(yù)測都是在預(yù)測均值。因此,我們希望均值對一個數(shù)據(jù)的水平有代表意義。但是只有變量是對稱分布的情況下,均值才具有代表性。而偏態(tài)分布下,均值容易被極值影響而產(chǎn)生偏離。這種情況下,中位數(shù)是一個不錯的選擇。由于中位數(shù)只考慮了從小到大排序后變量的位置信息,因此,信息使用程度上低于均值(均值既使用了位置信息,又使用了具體的數(shù)值信息),比均值穩(wěn)健,不會受極值的影響。而眾數(shù)就是這個變量取值頻次最多的值,眾數(shù)在分類變量中使用的居多。在連續(xù)變量中成為了查看數(shù)據(jù)質(zhì)量或錯誤編碼的一種方式,因為,連續(xù)變量取某個具體值的可能性較小,眾數(shù)出現(xiàn)的位置有可能具有特殊含義。比如,在收入數(shù)據(jù)中,眾數(shù)如果是“0”,這很有可能將缺失值錯誤編碼為“0”。
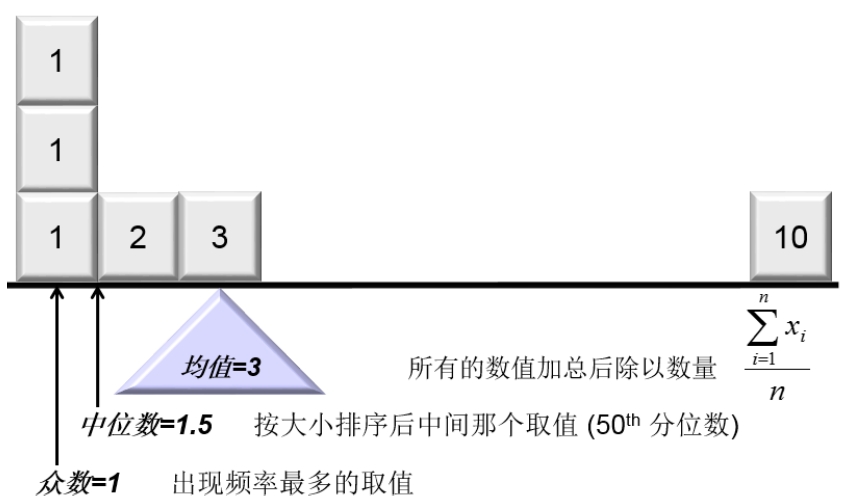
圖2-4
摘自:SAS公司《SAS? Enterprise Guide?:ANOVA,Regression,and Logistic Regression》
四分位數(shù)是另外一套表達變量位置信息的手段,其定義方式類似于中位數(shù),如圖2-5所示。中位數(shù)本身就是變量從大到小排序后,50%對應(yīng)的變量取值。而上下分位數(shù)分別是75%和25%對應(yīng)的變量取值。上下分位數(shù)的差值定義為四分位差,這是變量變化范圍的一種度量方法。四分位數(shù)和之后介紹的盒須圖有直接的關(guān)系。
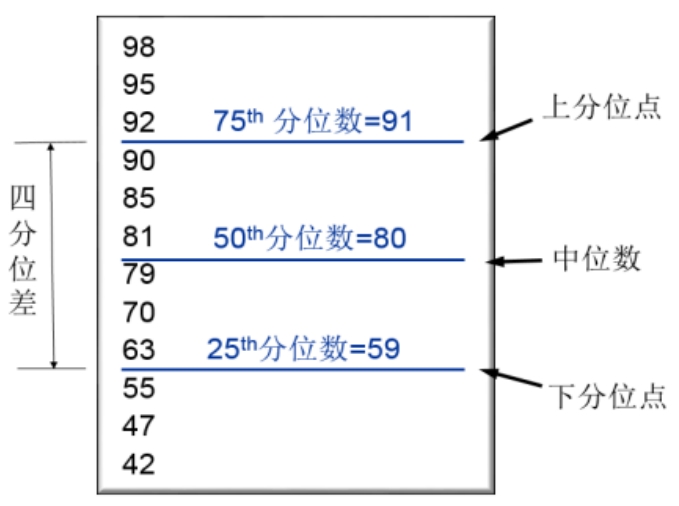
圖2-5
(2)離散程度
當(dāng)知道一個變量的“中心”水平統(tǒng)計量之后,還想知道這個指標(biāo)到底有多大的代表性。如果這個變量的變化范圍非常小,甚至是常數(shù),那么這個水平變量就非常有代表意義;如果這個變量的變化范圍非常大,那么水平指標(biāo)的代表性就相對下降。就居民收入而言,上海的收入變化范圍小。如果人均收入超過小康水平,那么可以認為上海市的貧困現(xiàn)象已經(jīng)不嚴重了。而四川的人均收入雖然也達到了小康水平,但是居民收入的差異較大,部分地區(qū)的貧困現(xiàn)象仍然較嚴重。因此,知道變量的離散程度是很有意義的。對經(jīng)濟而言,這個指標(biāo)代表發(fā)展不均勻程度。如表2-2所示,列出了4個常用的代表離散的變量。
表2-2 常用的代表離散程度的變量

方差公式為:
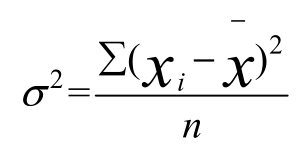
標(biāo)準(zhǔn)差公式為:
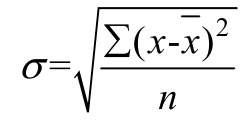
方差在統(tǒng)計學(xué)中也稱為二階中心距,實際是該變量每個取值到均值之間的距離均值。方差在很多參數(shù)統(tǒng)計的推導(dǎo)公式中出現(xiàn),但是在實際描述性統(tǒng)計中使用的不多。主要是方差的單位比較特殊,是原始單位的平方,一般人對方差大小沒有概念,不好理解。
標(biāo)準(zhǔn)差是描述分析中使用最多的,因為標(biāo)準(zhǔn)差的單位和原始變量相同。一旦用變量的每個變量的具體取值或均值除以標(biāo)準(zhǔn)差,則單位就被約去,只剩下無量綱的數(shù)值,這樣就可以進行跨變量的比較了。該方法稱為學(xué)生標(biāo)準(zhǔn)化、Z打分(Z-SCORE),是主成分分析、因子分析、聚類和標(biāo)準(zhǔn)化回歸中默認的標(biāo)準(zhǔn)化方法。T檢驗也是該標(biāo)準(zhǔn)化方法的一個直接運用。
(3)偏態(tài)程度(Skewness)
當(dāng)?shù)弥粋€變量的“中心”水平和離散程度統(tǒng)計量之后,我們還關(guān)心選取的“中心”水平統(tǒng)計量是否恰當(dāng)。這就要知道變量的偏度。如果變量的偏度為0,該變量就是對稱的,則選取均值作為水平的指標(biāo)是比較合適的;如果變量的偏度明顯大于或小于0,則選取均值是不恰當(dāng)?shù)摹1热纾用袷杖霐?shù)據(jù)由于存在明顯的右偏。因此,使用均值作為水平指標(biāo)是欠妥的,應(yīng)該使用中位數(shù),目前國際上也是選擇中位數(shù)。
偏態(tài)有兩種情況:一種是如圖2-6所示(左邊)的左偏,該變量在負的值部分嚴重拖尾;另一種是如圖2-6所示(右邊)的右偏,在正的值部分嚴重拖尾。在實際經(jīng)濟和商業(yè)數(shù)據(jù)分析中,右偏是比較普遍的狀態(tài)。比如,地區(qū)的居民收入、客戶購買產(chǎn)品的數(shù)量、金額和保險理賠額。
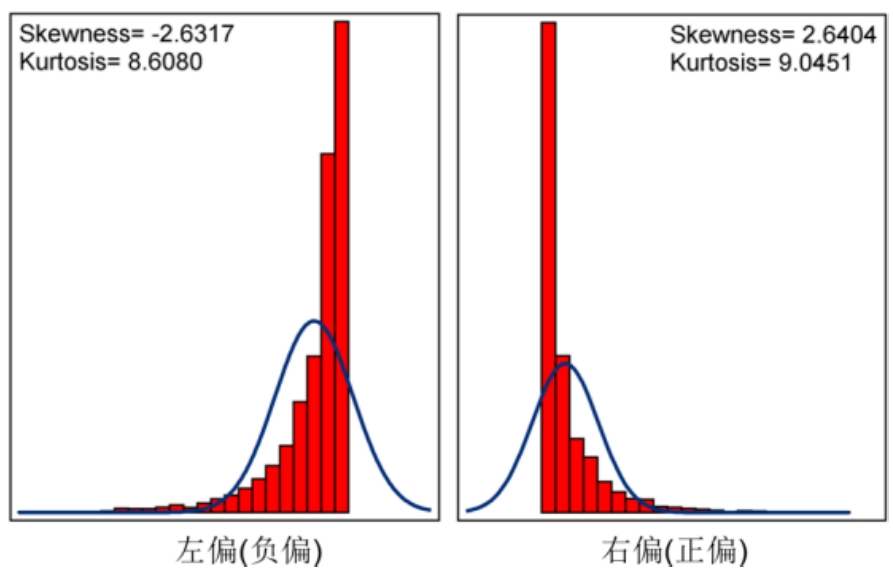
圖2-6
摘自:SAS公司《SAS? Enterprise Guide?:ANOVA,Regression,and Logistic Regression》
(4)峰度(Kurtosis)
峰度反應(yīng)的是變量向兩邊拖尾的情況,如圖2-7所示。相比正態(tài)分布而言,如果一個變量是尖峰的,則必然會導(dǎo)致兩邊拖尾情況更嚴重。反映到統(tǒng)計學(xué)中就會出現(xiàn)超過2倍標(biāo)準(zhǔn)差數(shù)值的概率會大于5%,超過3倍標(biāo)準(zhǔn)差數(shù)值的概率會大于1%。這表明出現(xiàn)較大偏離值的可能性提高了。資產(chǎn)收益率的峰度在金融研究中是比較受關(guān)注的,這表明了該資產(chǎn)的風(fēng)險分布情況,尾越厚,風(fēng)險越大。
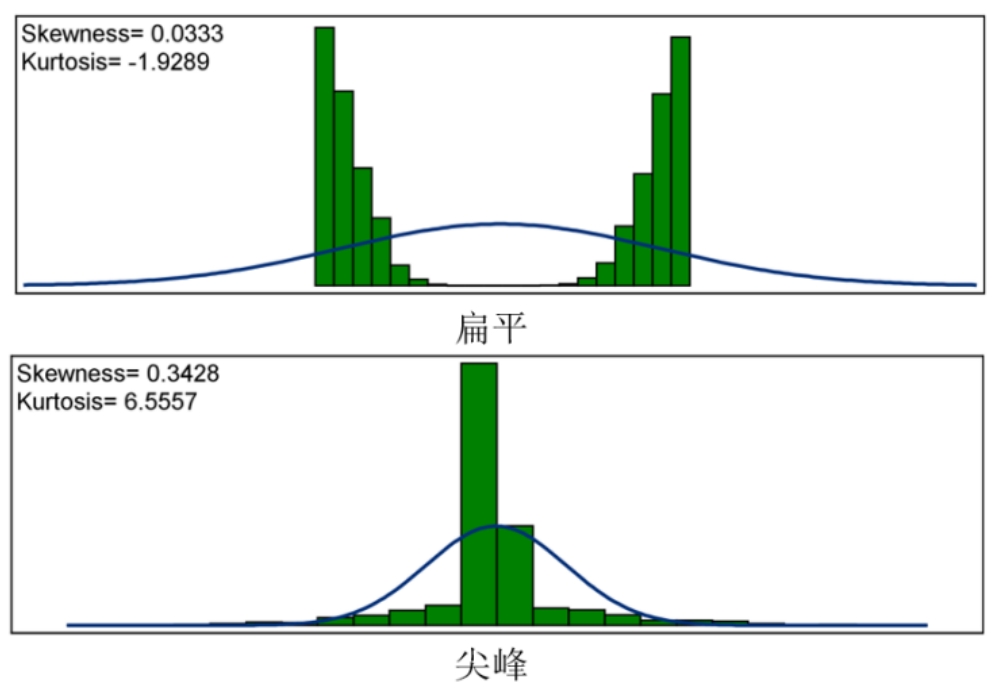
圖2-7
摘自:SAS公司《SAS? Enterprise Guide?:ANOVA,Regression,and Logistic Regression》
峰度(系數(shù))相當(dāng)于該變量的四階中心矩。正態(tài)分布的峰度(系數(shù))為常數(shù)3,均勻分布的峰度(系數(shù))為常數(shù)1.6。在SAS報告的結(jié)果中,將峰度值作減3處理,使正態(tài)分布的峰度為0。這與部分統(tǒng)計書和其他軟件是不同的,比如,Eviews默認的正態(tài)分布峰度為3。當(dāng)峰度值大于0時代表尖峰,小于0時代表扁平。在商業(yè)數(shù)據(jù)分析中,并不太重視變量峰度的情況。因此,大家只要了解一下就可以了,深度的運用主要是在金融行業(yè)。
 圖形
圖形
(1)條形圖
條形圖是一個很好展現(xiàn)變量分布情況的方式,但是連續(xù)變量不可能做出條形圖,因為連續(xù)變量如果精度足夠大的話,每個取值出現(xiàn)的頻數(shù)應(yīng)該只有一次。但是可以采用將連續(xù)變量分箱的方法做直方圖。這樣,每個柱代表一個分箱,柱高為在這個分箱中的取值出現(xiàn)的次數(shù)或百分比,分箱的數(shù)量和間隔可以自定義,如圖2-8所示。
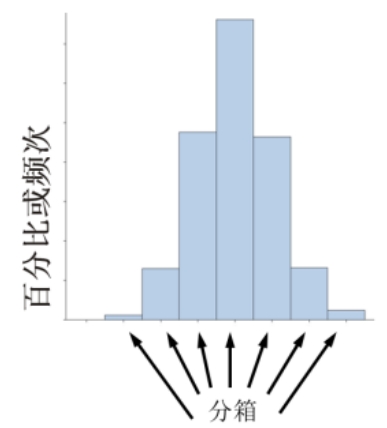
圖2-8
既然介紹變量的分布情況,就要介紹一下正態(tài)分布。首先,正態(tài)分布是關(guān)于均值左右對稱的,呈鐘形,如圖2-9所示。其次,正態(tài)分布的均值和標(biāo)準(zhǔn)差具有代表性,只要知道其均值和標(biāo)準(zhǔn)差,這個變量的分布情況就完全知道了。在正態(tài)分布中,均值=中位數(shù)=眾數(shù)。
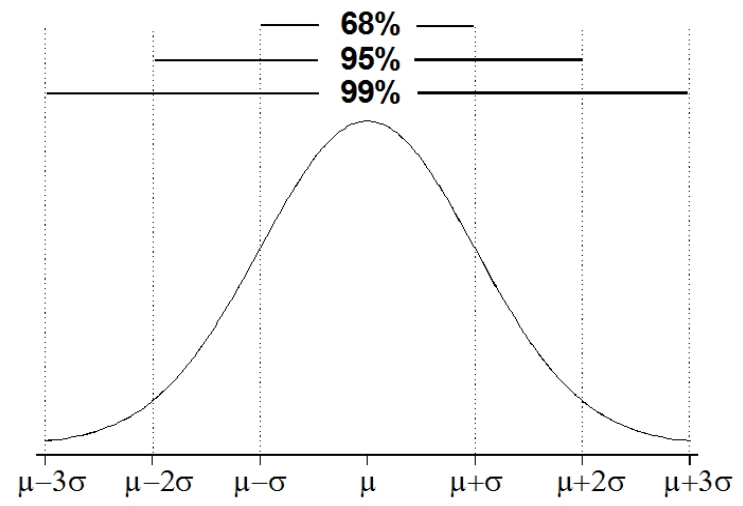
圖2-9
而且正態(tài)分布的標(biāo)準(zhǔn)差和曲線下面積有一個比較好記憶的關(guān)系。比如,變量取值距離均值兩倍標(biāo)準(zhǔn)差內(nèi)出現(xiàn)的概率為95%。這表明該變量出現(xiàn)大于均值加兩倍標(biāo)準(zhǔn)差的概率為2.5%,小于均值減兩倍標(biāo)準(zhǔn)差的概率也為2.5%。
如圖2-10所示,提供了其他常見分布的分布曲線。依照偏度由低到高分別是正態(tài)分布、泊松分布、伽瑪分布和對數(shù)正態(tài)分布。其中對數(shù)正態(tài)分布在統(tǒng)計分析中運用最為廣泛。顧名思義,這種類型的分布在取對數(shù)之后服從正態(tài)分布。因為其具有這樣的良好屬性,在精確度要求并不嚴格的統(tǒng)計分析中,經(jīng)常對偏態(tài)分布首先進行對數(shù)轉(zhuǎn)換。而對于精確度要求較高的統(tǒng)計分析領(lǐng)域,則采用有針對性的分析方式,比如泊松回歸和伽瑪回歸。
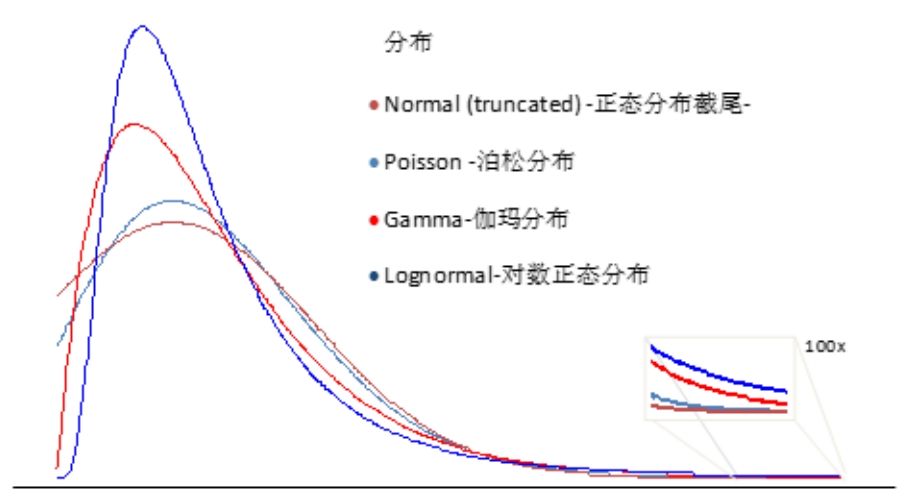
圖2-10
(2)盒須圖
盒須圖相對于直方圖而言,提供的信息更精煉。它提供了中位數(shù)、均值、上下分位點的信息,這不但可以了解變量的中心水平,還可以了解變量的變化范圍。其中需要說明的是最大值和最小值,它們不是變量的最大值和最小值。如圖2-11所示,以盒須圖中的最大值為例,從上分位點加上1.5倍的內(nèi)分位距(IQR),該變量在這個范圍內(nèi)的最大取值被稱為最大值,超過1.5倍的內(nèi)分位距的取值被稱為離群值。對于右偏態(tài)數(shù)據(jù),會出現(xiàn)上面“須子”長,下面“須子”短的情況。
盒須圖在研究分類變量和連續(xù)變量關(guān)系時,其重要性可以和散點圖(反應(yīng)兩個連續(xù)變量關(guān)系)相提并論。如圖2-12所示,不但可以比較每組間中心水平的變化,還可以比較每組間變化范圍與偏態(tài)的變化。其展示效果明顯優(yōu)于直方圖。因此,盒須圖是在做方差分析和回歸之前重要的數(shù)據(jù)關(guān)系探索方法。

圖2-11
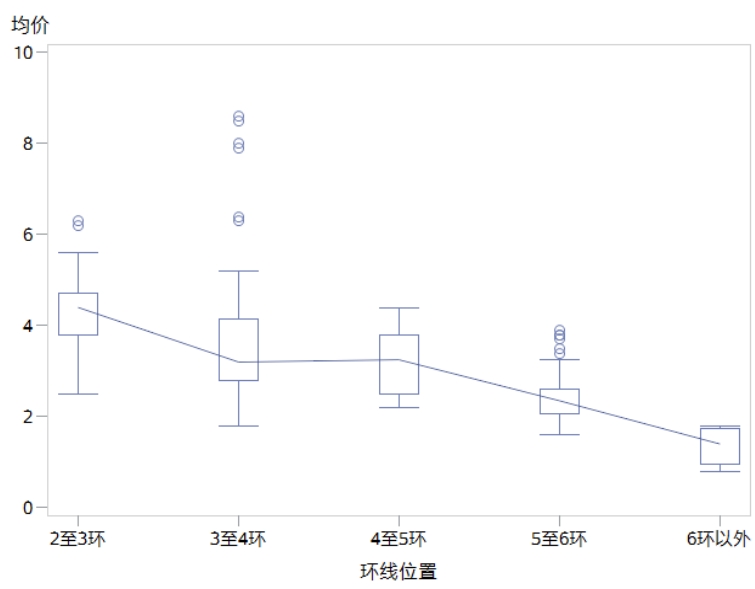
圖2-12
(3)P-P圖和Q-Q圖
P-P圖原理:用于確定實際累積概率是否與理論分布累積概率匹配,如圖2-13所示。如果選定變量與檢驗的理論分布匹配,則圓點聚集在(理論分布計算的)直線周圍,與理論分布保持一致。圓點表示實際數(shù)據(jù)的累積概率,直線表示理論概率,兩者偏離小,則符合正態(tài)分布,反之則不符合。
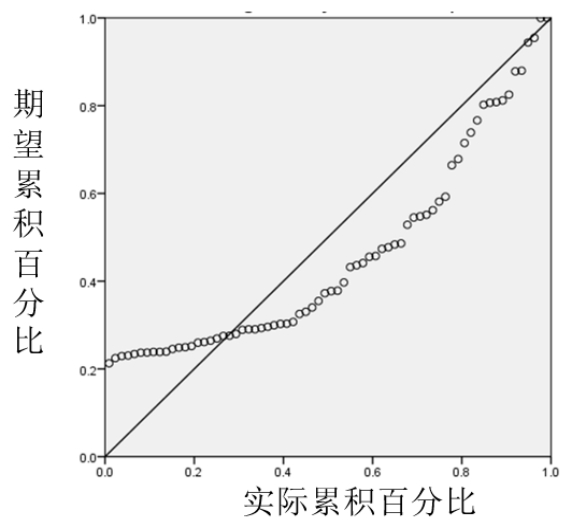
圖2-13
Q-Q圖相對P-P圖來說原理很相似,使用的是實際百分位數(shù)與理論百分位數(shù)進行繪制圖形。一般來說更穩(wěn)健一點,但問題是沒有明確的經(jīng)驗界值,所以被使用的頻率較少。Q-Q圖輸出結(jié)果的解讀方法與P-P圖相同,這里不再呈現(xiàn)。
【案例分析2-1】“PROFIT”中存放著公司每筆訂單的產(chǎn)品銷售情況,請分析一下產(chǎn)品的利潤分布情況。
(1)首先雙擊“PROFIT”表,打開“查詢生成器”對話框,按照產(chǎn)品分別對產(chǎn)品利潤進行加總,如圖2-14所示。
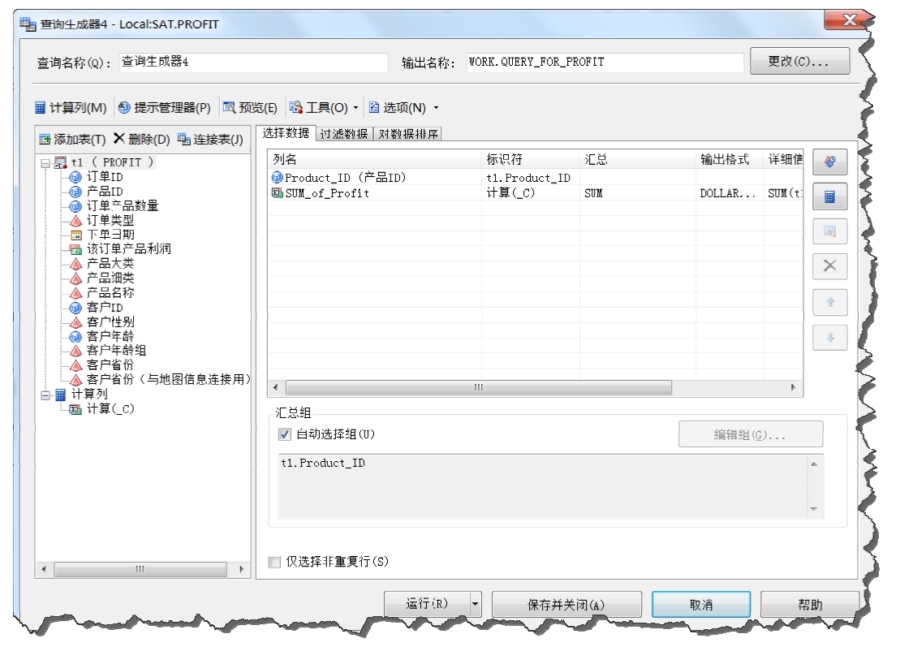
圖2-14
(2)在新生成的表中,打開“描述→匯總統(tǒng)計量”對話框,將每個產(chǎn)品的利潤(SUM_of_Profit)放入分析變量的位置,如圖2-15所示。該過程背后調(diào)用的是“MEANS”過程。
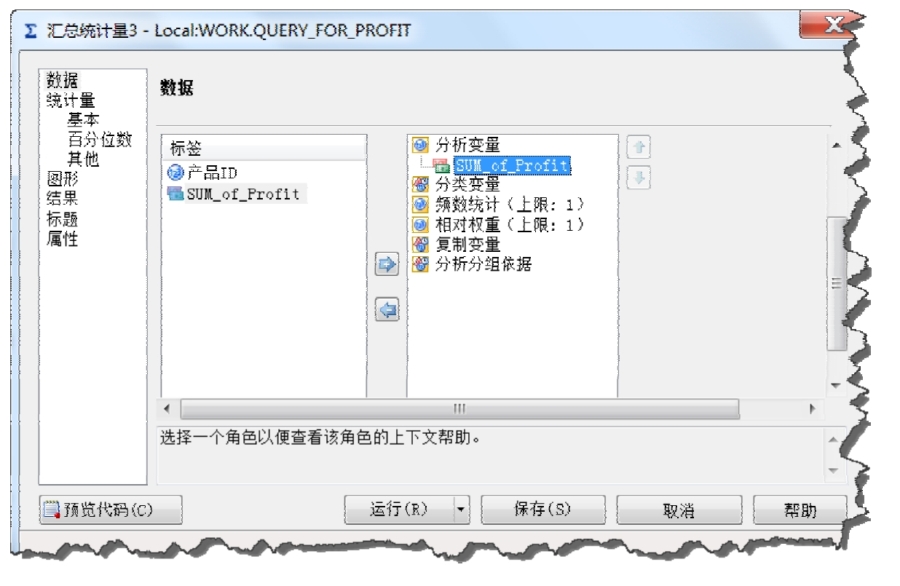
圖2-15
(3)在“圖形”頁面中選擇需要的圖形,如圖2-16所示。
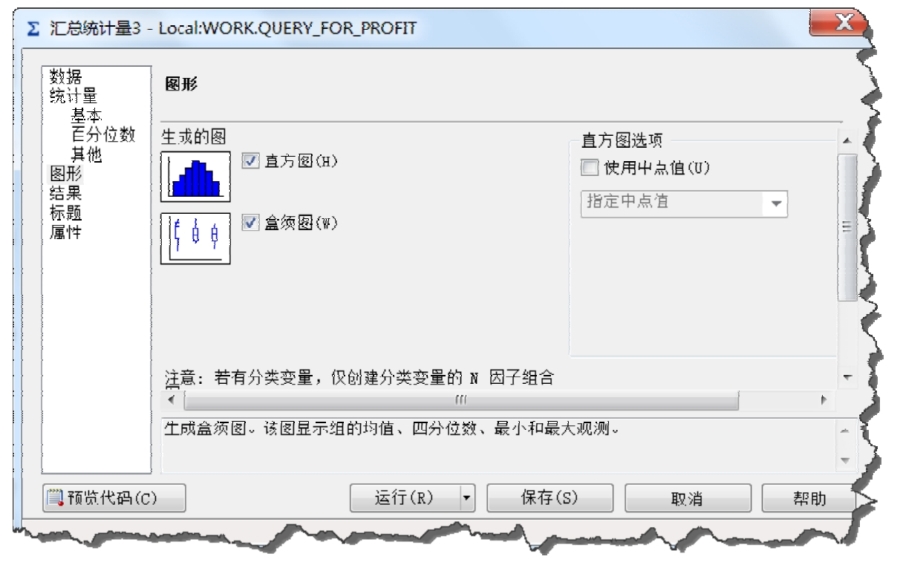
圖2-16
(4)如果需要檢驗該變量是否服從正態(tài)分布,需要打開“描述→分布分析”對話框,如圖2-17所示。該對話框和“匯總統(tǒng)計量”對話框類似,但是背后調(diào)用的是“UNIVARIATE”過程,它的功能更強大,提供的統(tǒng)計量更豐富。
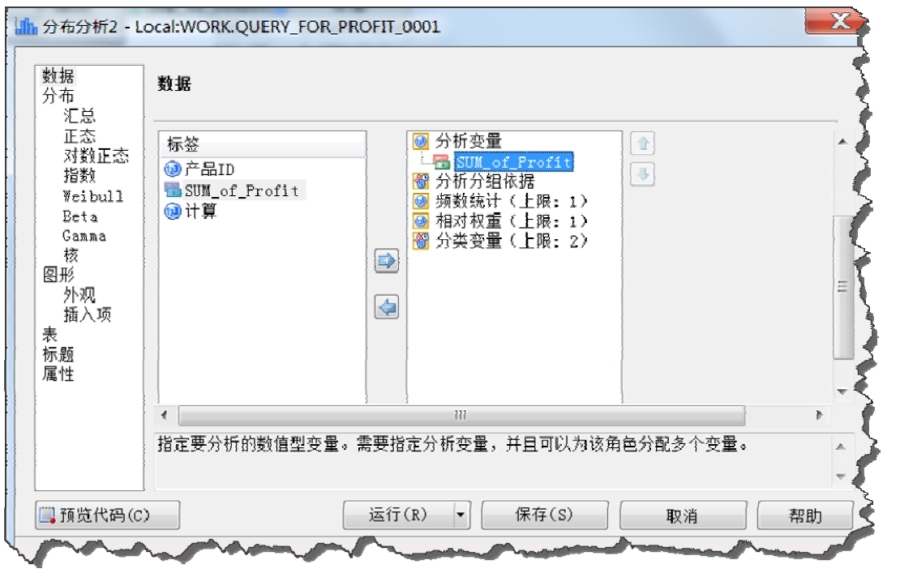
圖2-17
【案例分析2-2(SPSS操作)】
在SPSS中,完成SAS EG“描述→匯總統(tǒng)計量”對等的菜單是“分析→描述→頻次”;完成SAS EG“查詢生成器”中分類匯總的對等菜單是“分析→描述→頻次”。以下分別敘述。
(1)對數(shù)據(jù)進行描述統(tǒng)計,選擇“分析→描述→頻次”選項,SPSS中的這個菜單功能很強大,不但可以分析連續(xù)變量,還可以分析分類變量,其操作如圖2-18所示。
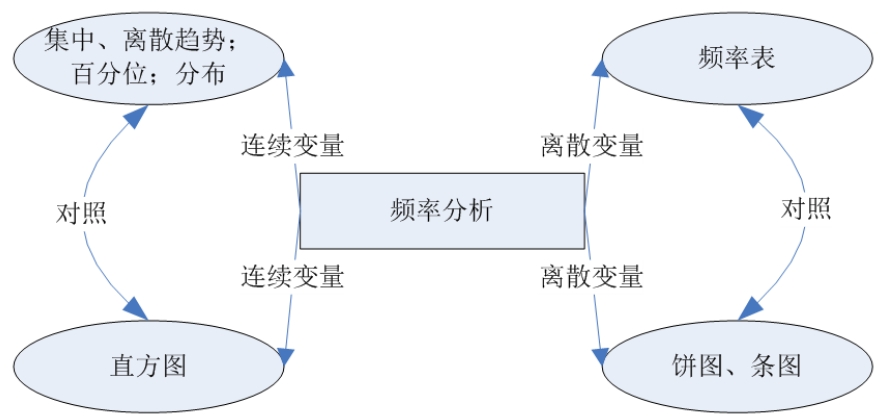
圖2-18
比如當(dāng)分析連續(xù)變量時,就要取消勾選“顯示頻率表格”復(fù)選框,如圖2-19所示。
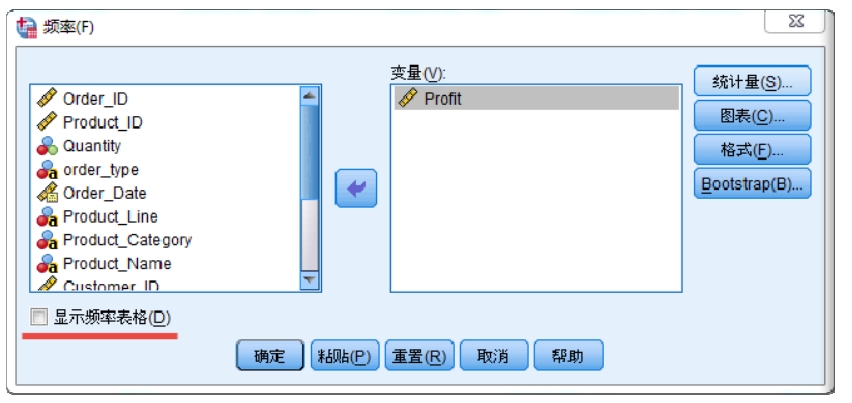
圖2-19
在“統(tǒng)計量”子對話框中,選擇所需的統(tǒng)計量,如“均值”、“中位數(shù)”、“標(biāo)準(zhǔn)差”等,如圖2-20所示。執(zhí)行后的結(jié)果,如圖2-21所示。
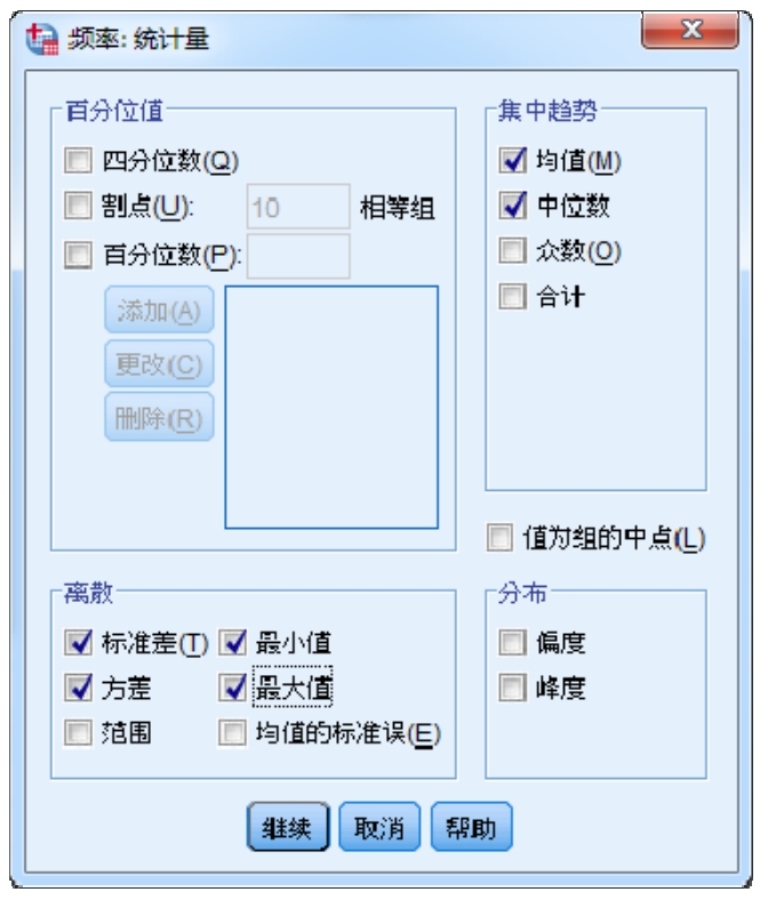
圖2-20
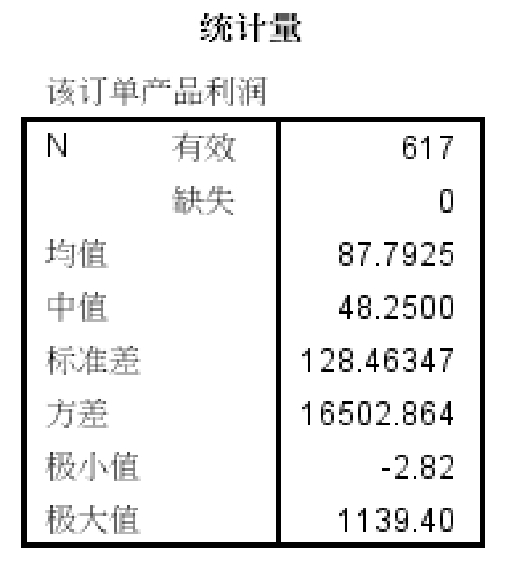
圖2-21
如果需要按照產(chǎn)品大類對利潤進行分別的表述,需要事先對數(shù)據(jù)分組。方法是選擇“數(shù)據(jù)→拆分文件”,在彈出的“分割文件”對話框中,將分組依據(jù)變量“Product_line”選入分組方式中,并且選中“比較組”單選按鈕,如圖2-22所示。
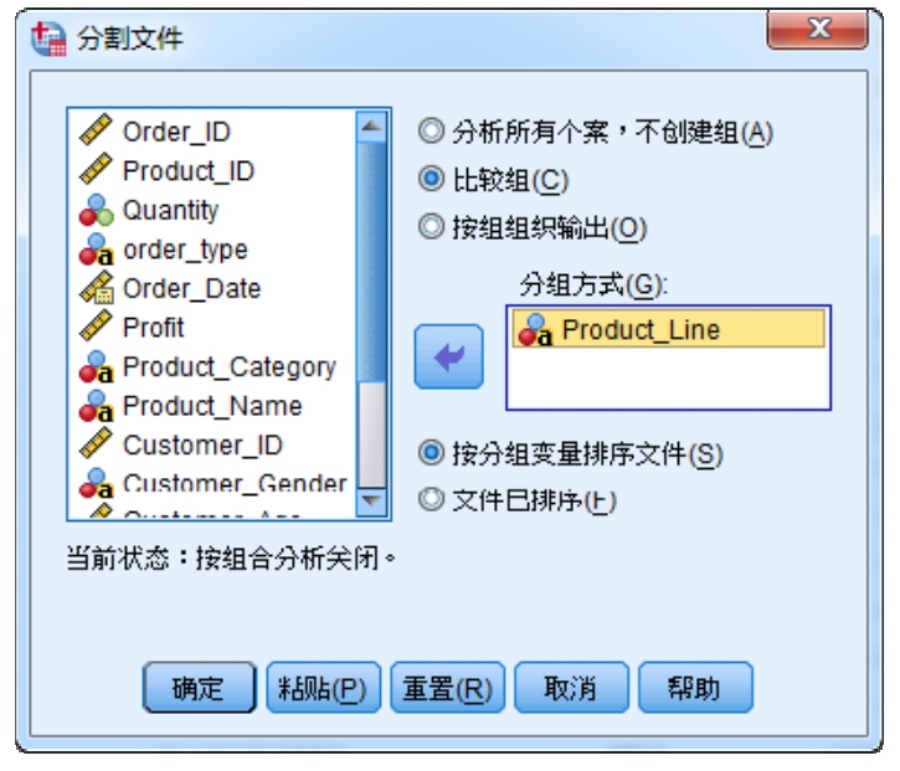
圖2-22
經(jīng)過這樣的操作之后,SPSS數(shù)據(jù)框的右下角會出現(xiàn)“拆分條件Product_Line”的顯示。之后對數(shù)據(jù)所有的操作都是按照“Product_line”分組展示。請讀者再次做一遍對“的Profit”變量的描述分析。
(2)打開“數(shù)據(jù)→分類匯總”對話框,按照產(chǎn)品大類對產(chǎn)品利潤進行匯總,將產(chǎn)品大類選入分組變量,將該訂單產(chǎn)品利潤選入?yún)R總變量,默認匯總方式為計算均值,單擊“函數(shù)”按鈕,在摘要統(tǒng)計量中可以選擇總和,對利潤進行加總計算。默認保存到活動數(shù)據(jù)集,該處選擇創(chuàng)建一個新的數(shù)據(jù)集“產(chǎn)品大類利潤匯總”,然后將匯總結(jié)果保存到此處,如圖2-23所示。
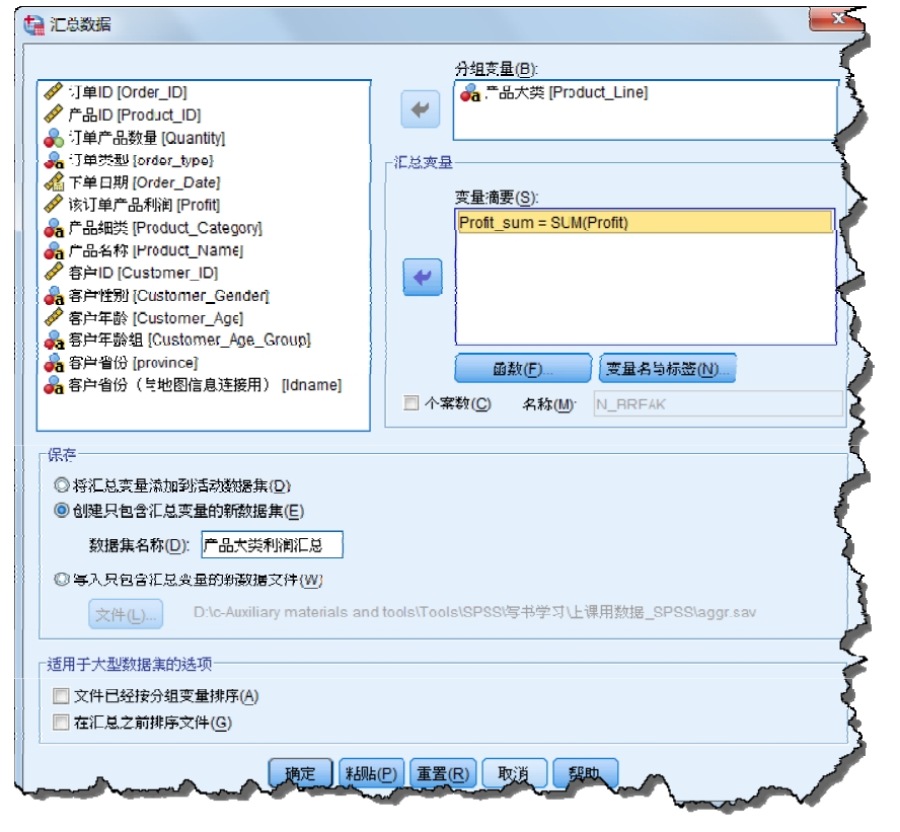
圖2-23
(3)在新建表中打開“圖形→圖表構(gòu)建程序”對話框,選擇需要的圖形,將相應(yīng)變量放入坐標(biāo)軸,如圖2-24所示。
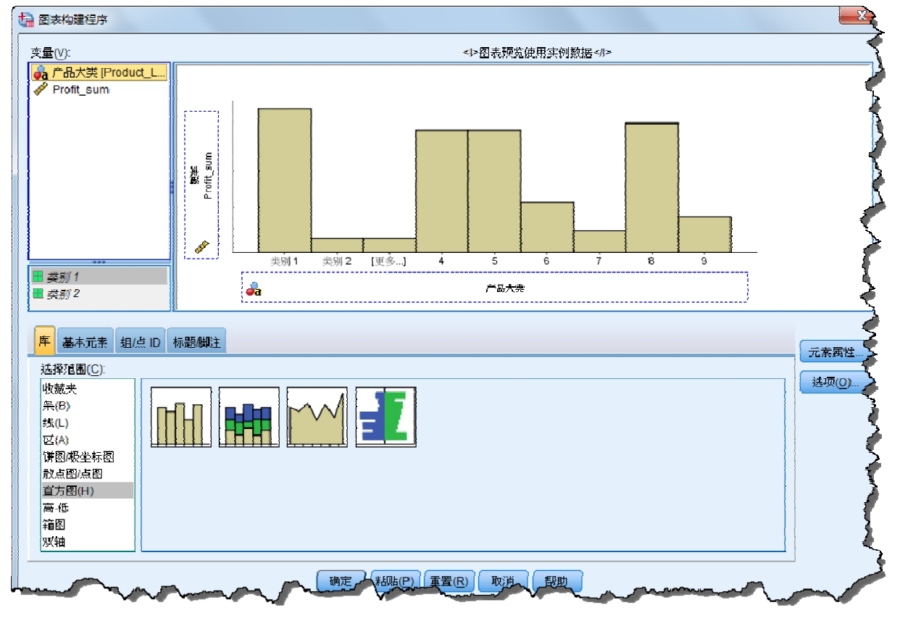
圖2-24
(4)如果需要檢驗該變量是否服從正態(tài)分布,可以通過制作P-P圖或Q-Q圖實現(xiàn),下面以P-P圖為例。在新建數(shù)據(jù)集里打開“分析→描述統(tǒng)計→P-P圖”對話框,利潤匯總選入變量,檢驗分布默認正態(tài)即可,如圖2-25所示。
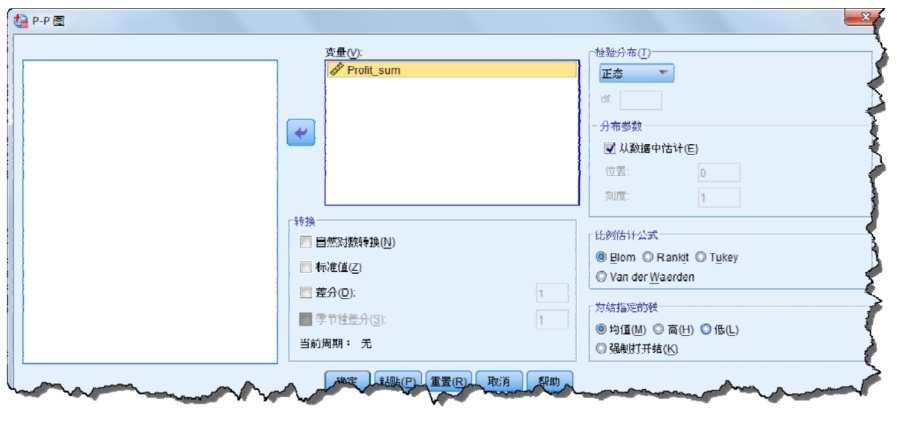
圖2-25
 制作報表
制作報表
制作報表就是根據(jù)數(shù)據(jù)類型,選取合適統(tǒng)計量并進行展現(xiàn)的過程。如圖2-26所示,表現(xiàn)的是一個比較全面的二維表模版,而三維表只不過是簡單的疊加而已。水平軸和垂直軸分別是兩個分類變量。單元格中存放的是某個變量的統(tǒng)計量,如果單元格中沒有放入任何變量時,則單元格展現(xiàn)的是頻次或百分比等指標(biāo)。如果放入了某個連續(xù)變量,則單元格展現(xiàn)的就是這個連續(xù)變量的某個統(tǒng)計量。比如均值、總合等。
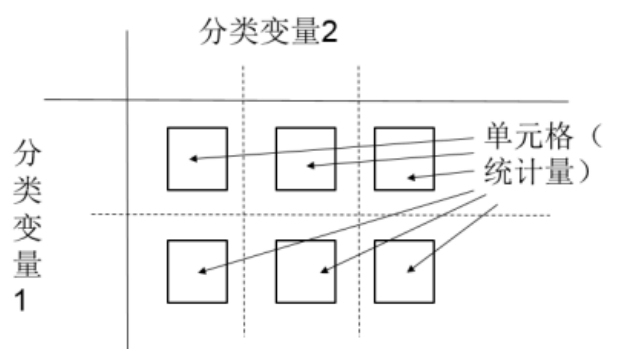
圖2-26
將二維表模版的內(nèi)容進行縮減,分別可以得到單因子頻數(shù)、表分析、匯總統(tǒng)計量和匯總表任務(wù),具體說明如下。
(1)單因子頻數(shù):僅分析單個分類變量的分布情況,提供每個水平的頻次、百分比和累積值,如圖2-27所示。
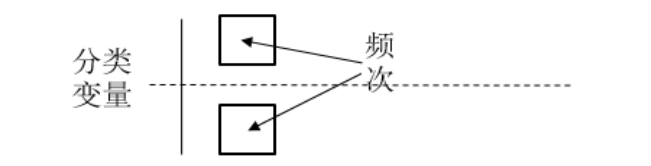
圖2-27
(2)表分析:分析兩個分類變量的聯(lián)合分布情況,提供每個單元格的頻次、百分比和邊沿分布情況,如圖2-28所示。
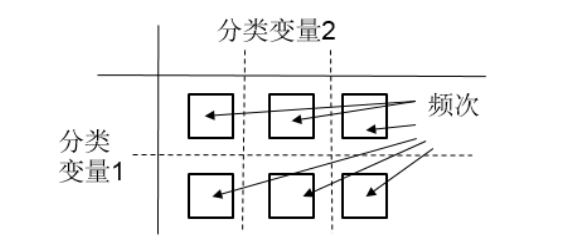
圖2-28
(3)匯總統(tǒng)計量:按照某個分類變量分組,對連續(xù)變量進行描述性統(tǒng)計。分布分析也提供了類似的功能,如圖2-29所示。
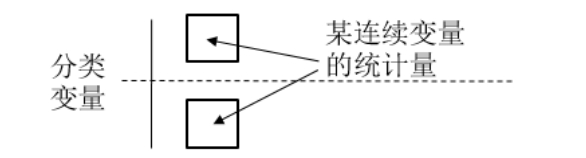
圖2-29
(4)匯總表:按照兩個或多個分類變量分組,對某個連續(xù)變量進行描述性統(tǒng)計,如圖2-30所示。
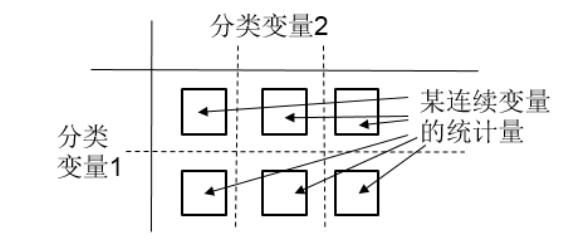
圖2-30
為了便于讀者選取合適的功能,如圖2-31所示,給出了單變量的描述下拉菜單中每個命令的功能。

圖2-31
- 程序員面試白皮書
- Mastering Adobe Captivate 2017(Fourth Edition)
- iOS 9 Game Development Essentials
- vSphere High Performance Cookbook
- Django開發(fā)從入門到實踐
- Hands-On Data Structures and Algorithms with JavaScript
- C#程序設(shè)計(慕課版)
- Java FX應(yīng)用開發(fā)教程
- Object-Oriented JavaScript(Second Edition)
- Magento 1.8 Development Cookbook
- JavaScript by Example
- Bootstrap 4:Responsive Web Design
- 從0到1:Python數(shù)據(jù)分析
- RISC-V體系結(jié)構(gòu)編程與實踐(第2版)
- C語言開發(fā)基礎(chǔ)教程(Dev-C++)(第2版)