1.6　降維

降維算法即將高維數據投射到低維空間，并盡可能地保留最多的信息。這類算法既可以用于去除高維數據的冗余信息，也可以用于數據的可視化。比如我們可以使用降維算法將鳶尾花數據集的數據分布情況直觀地展現出來。鳶尾花數據本身有4個特征，也就是一個四維空間的數據，因為四維空間是無法直接觀測的，所以需要將數據降到三維空間才可以查看。

1.6.1　PCA降維

首先可以嘗試使用最常用的降維方法PCA（主成分分析）對鳶尾花數據集進行降維展示，將數據集從四維降到三維的代碼如下：

>>> from sklearn.datasets import load_iris
>>> from sklearn.decomposition import PCA
>>> from mpl_toolkits.mplot3d import Axes3D
>>> data = load_iris()
>>> x = data['data']
>>> y = data['target']
>>> # n_components表示主成分維度
>>> pca = PCA(n_components=3)
>>> # 將數據降成三維
>>> x_3d = pca.fit_transform(x)
>>> fig = plt.figure()
>>> plt.subplot(121)
<matplotlib.axes._subplots.AxesSubplot object at 0x000000000FDA3860>
>>> ax = Axes3D(fig)
>>> for i,item in enumerate(x_3d):
...     ax.scatter(item[0],item[1],item[2],color = colors[y[i]],marker = markers[y[i]])
...
>>> plt.show()

上述代碼中的fit_transform方法將模型訓練和數據轉換合并在一起，方便調用。降維后，三維鳶尾花數據如圖1-11所示。

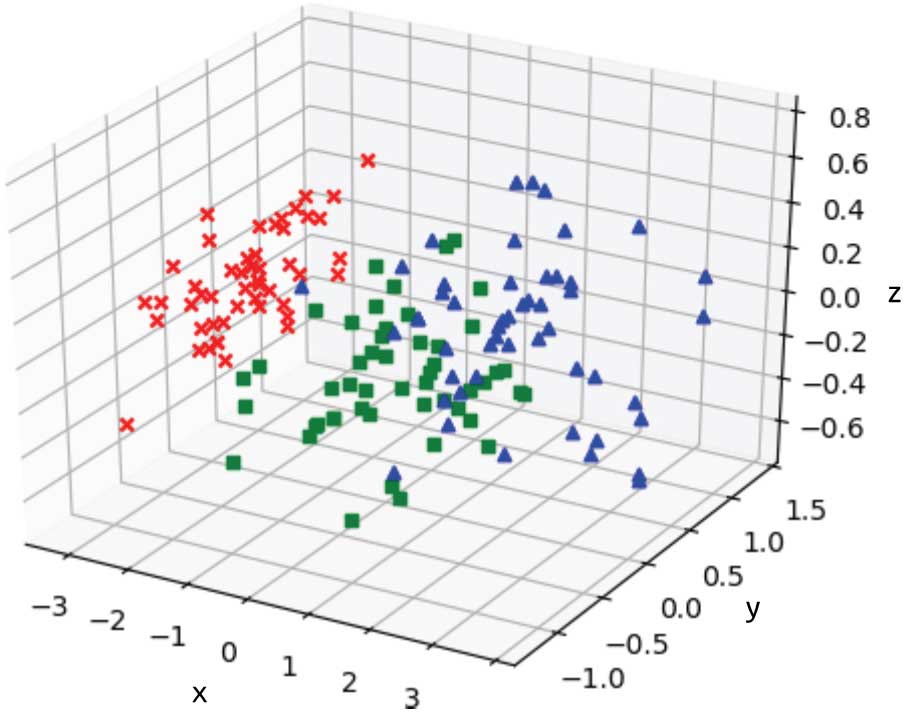
圖 1-11　使用PCA將鳶尾花數據集降維至三維

在圖1-11所示的三維空間中我們可以看到，鳶尾花數據的3個類別之間呈現出相互分離的狀態，可以較容易地找到數據的分類界面。

接下來繼續把數據降到二維空間，查看有何變化，將鳶尾花數據集從四維降到二維的代碼如下，降維后的結果如圖1-12所示：

>>> pca2d = PCA(n_components=2)
>>> x_2d = pca2d.fit_transform(x)
>>> plt.figure()
<Figure size 640x480 with 0 Axes>
>>> for i,item in enumerate(x_2d):
...     plt.scatter(item[0],item[1],color = colors[y[i]],marker = markers[y[i]])
...
>>> plt.show()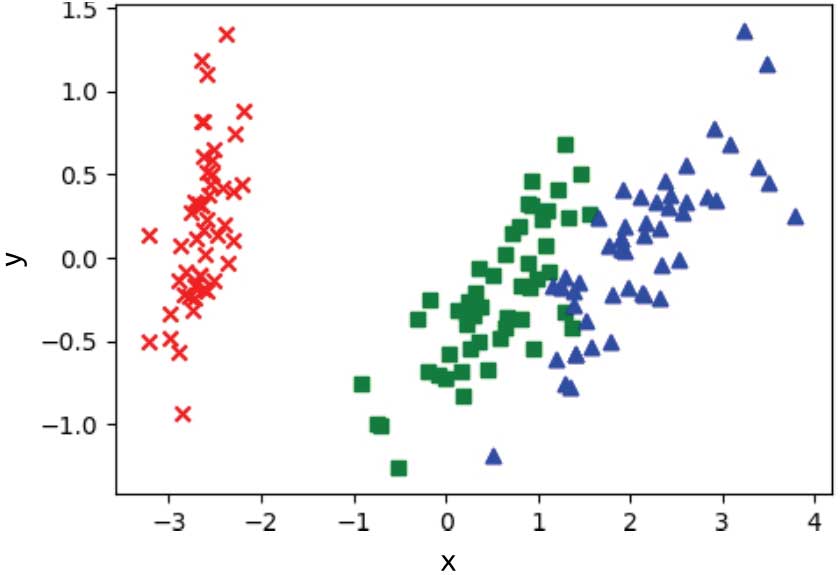

圖 1-12　使用PCA將鳶尾花數據集降維至二維

從圖1-12可以看到，降到二維之后，鳶尾花數據集仍然具有很好的可分性，這就達到了降維過程中盡量保留有用信息的要求。

最后再嘗試把數據降到一維，從四維降到一維的代碼如下，降維后的結果如圖1-13所示：

>>> pca1d = PCA(n_components=1)
>>> x_1d = pca1d.fit_transform(x)
>>> plt.figure()
<Figure size 640x480 with 0 Axes>
>>> for i,item in enumerate(x_1d):
...     plt.scatter(item[0],0,color = colors[y[i]],marker = markers[y[i]])
...
>>> plt.show()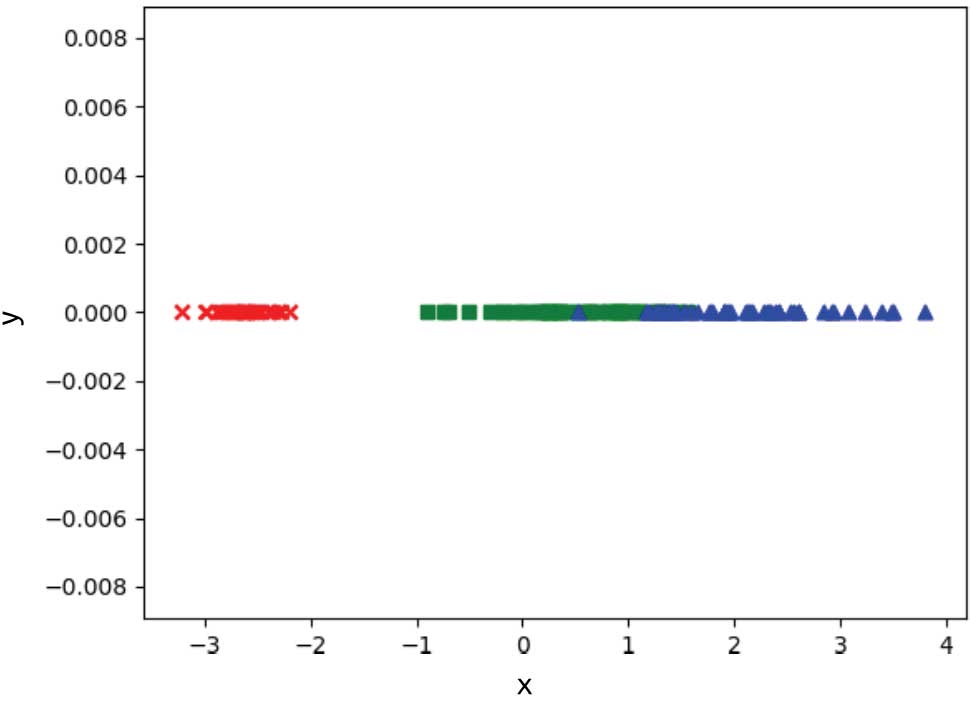

圖 1-13　使用PCA將鳶尾花數據集降維至一維

從圖1-13中可以看到，降到一維之后，鳶尾花數據集中的兩個分類出現了比較明顯的交疊現象，不能通過某個閾值將數據很好地進行分類。

1.6.2　LDA降維

除了PCA，sklearn還提供了一個降維方法：LDA（線性判別分析）。使用LDA也可以對鳶尾花數據集進行降維可視化。

因為LDA只能將數據降維到 [1, 類別數-1)，所以在鳶尾花任務中，無法使用LDA將數據降維到三維，最高只能做二維展示。降維展示代碼如下，降維結果如圖1-14所示：

>>> from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA
>>> lda = LDA(n_components=2)
>>> x_2d = lda.fit_transform(x,y)
>>> plt.figure()
<Figure size 640x480 with 0 Axes>
>>> for i,item in enumerate(x_2d):
...     plt.scatter(item[0],item[1],color = colors[y[i]],marker = markers[y[i]])
...
>>> plt.show()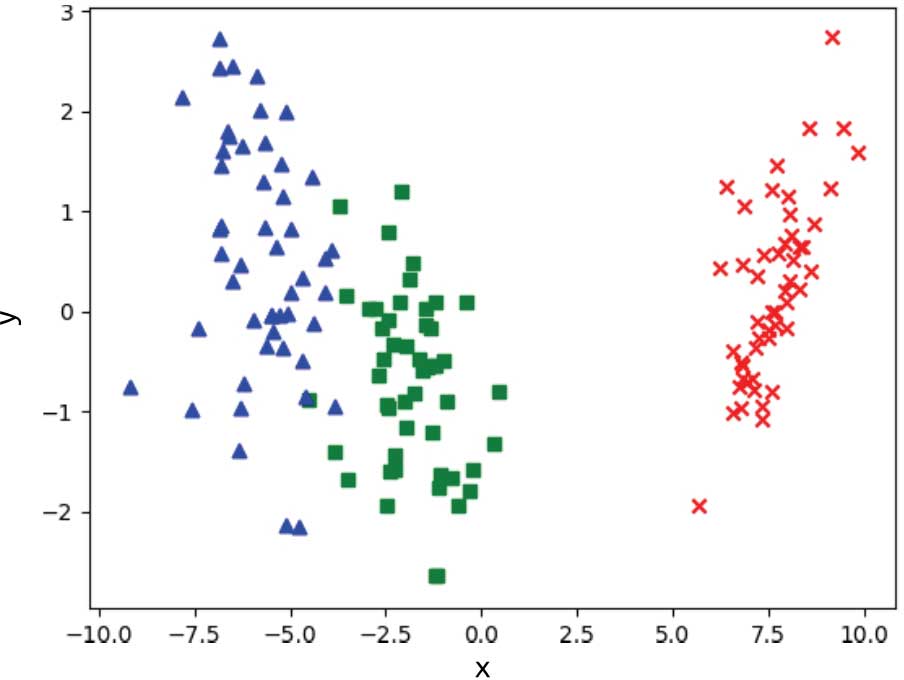

圖 1-14　使用LDA將鳶尾花數據集降維至二維

對比圖1-14與圖1-12，也可以看出，使用LDA降維之后的數據比使用PCA降維之后的數據的可分性更好。

那么繼續做一維降維，會得到什么樣的效果呢？以下是使用LDA進行四維轉一維的代碼，降維結果如圖1-15所示：

>>> lda = LDA(n_components=1)
>>> x_1d = lda.fit_transform(x,y)
>>> plt.figure()
<Figure size 640x480 with 0 Axes>
>>> for i,item in enumerate(x_1d):
...     plt.scatter(item[0],0,color = colors[y[i]],marker = markers[y[i]])
...
>>> plt.show()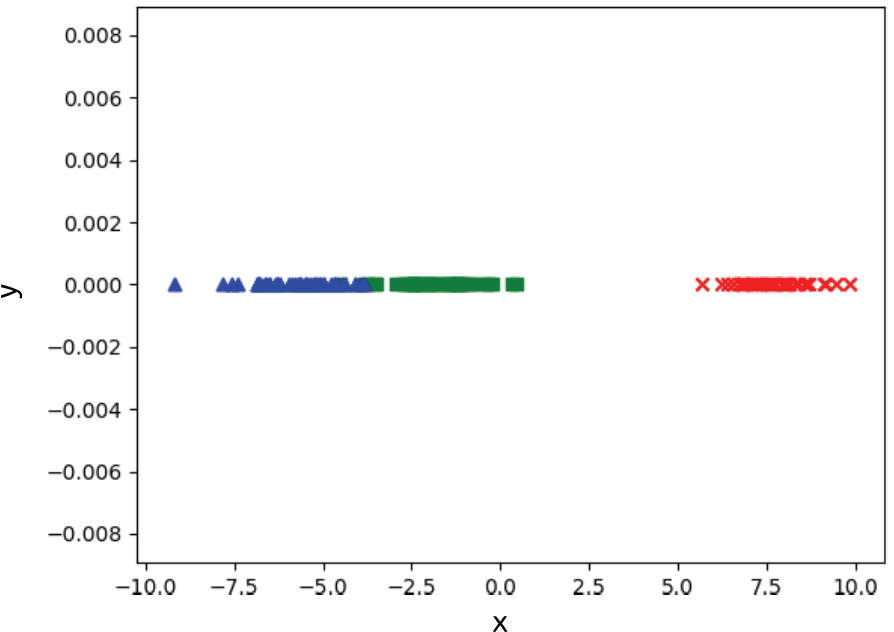

圖 1-15　使用LDA將鳶尾花數據集降維至一維

從圖1-15中可以看到，將鳶尾花數據集降維到一維之后，雖然有兩個類別相距較近，但是幾乎看不出來任何重疊。

兩種方法最大的區別是PCA是無監督學習算法，而LDA是監督學習算法，這一點從二者fit_transform方法的輸入參數可以看出。

PCA的降維原則是保留方差較大的維度，降維方差較小的維度，而LDA的降維原則是保證降維后，類內方差最小，類間方差最大。因此，LDA降維之后的數據可分性較強。可見，在有標簽的情況下，應該盡量使用LDA進行降維或者可視化。