3.2 誤差分析和方程組的條件數(shù)

誤差問題是不可避免的，在大量的數(shù)據(jù)樣本中，如果能去掉部分可能造成很大誤差的樣本，那么應(yīng)用矩陣得到的結(jié)果的可靠性將大大加強(qiáng)。條件數(shù)事實(shí)上表示了矩陣計(jì)算對誤差的敏感性。條件數(shù)越小，數(shù)值穩(wěn)定性越好。

對一個(gè)數(shù)值問題本身，如果輸入數(shù)據(jù)的微小擾動（即誤差）就會引起輸出數(shù)據(jù)（即問題解）出現(xiàn)很大的相對誤差，那么這就是病態(tài)問題。條件數(shù)是線性方程組Ax=b的解對b中的誤差或不確定度的敏感性的度量。

3.2.1 向量和矩陣范數(shù)

范數(shù)是數(shù)值分析中的一個(gè)概念，它是向量或矩陣大小的一種度量，在工程計(jì)算中有著重要的作用。

1.向量范數(shù)

兩個(gè)點(diǎn)之間的距離為向量元素之差的范數(shù)。在幾何學(xué)上，點(diǎn)之間的距離等于從一個(gè)點(diǎn)延伸到另一個(gè)點(diǎn)的向量的值。

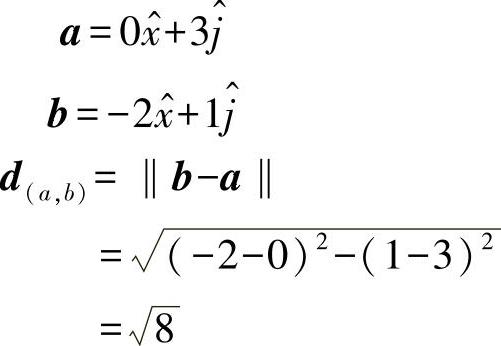
2.常規(guī)向量范數(shù)

具有n個(gè)元素的向量v的p-范數(shù)的常規(guī)定義是

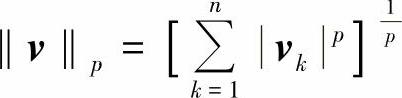
其中，p是任何正的實(shí)數(shù)值、Inf或-Inf。這些值得關(guān)注的p值包括：

?如果p=1，則所得的1-范數(shù)是向量元素的絕對值之和。

?如果p=2，則所得的2-范數(shù)是向量的模或歐幾里得距離。

?如果p=Inf，則‖v‖∞=max_i（|v（i）|）。

?如果p=-Inf，則‖v‖-∞=min_i（|v（i）|）。

于向量x∈Rⁿ，常用的向量范數(shù)有以下幾種。

?x的∞-范數(shù)：。

?x的1-范數(shù)：。

?x的2-范數(shù)（歐氏范數(shù)）：。

?x的p-范數(shù)：。

在MATLAB中，vecnorm命令用來求解向量范數(shù)和計(jì)算矩陣中每列的范數(shù)，它的使用格式見表3-4。

表3-4 vecnorm命令的使用格式

例3-7：計(jì)算向量的1-范數(shù)。

解：MATLAB程序如下。

例3-8：計(jì)算向量的n-范數(shù)。

解：MATLAB程序如下。

例3-9：計(jì)算矩陣的列范數(shù)。

解：MATLAB程序如下。

3.矩陣范數(shù)

對于矩陣A∈R^m×n，常用的矩陣范數(shù)有以下幾種。

?A的行范數(shù)（∞-范數(shù)）：。

?A的列范數(shù)（1-范數(shù)）：。

?A的歐氏范數(shù)（2-范數(shù)）：，其中λ_max（A^TA）表示A^TA的最大特征值。

?A的Frobenius范數(shù)（F-范數(shù)）：。

在MATLAB中，norm命令用來求解向量范數(shù)和矩陣范數(shù)，它的使用格式見表3-5。

表3-5 norm命令的使用格式

（1）最大絕對列之和

mxn矩陣X（m，n>=2）的最大絕對列之和由定義。

（2）最大絕對行之和mxn矩陣X（m，n>=2）的最大絕對行之和由定義。

（3）Frobenius范數(shù)

mxn矩陣X（m，n>=2）的Frobenius范數(shù)由定義。

例3-10：計(jì)算兩個(gè)點(diǎn)之間的歐幾里得距離。

解：MATLAB程序如下。

在MATLAB中，normest命令用來求解2-范數(shù)估值，它的使用格式見表3-6。

表3-6 normest命令的使用格式

例3-11：常用的矩陣函數(shù)示例。

解：MATLAB程序如下。

3.2.2 矩陣條件數(shù)

矩陣的條件數(shù)在數(shù)值分析中是一個(gè)重要的概念，在工程計(jì)算中也是必不可少的，它用于刻畫一個(gè)矩陣的“病態(tài)”程度。

對于非奇異矩陣A，其條件數(shù)的定義為

cond（A）_v=‖A^-1‖_v‖A‖_v，其中v=1，2，…，F。

它是一個(gè)大于或等于1的實(shí)數(shù)，當(dāng)A的條件數(shù)相對較大，即cond（A）_v>>1時(shí)，矩陣A是“病態(tài)”的，反之是“良態(tài)”的。

矩陣條件數(shù)估計(jì)：

計(jì)算A的1-范數(shù)條件數(shù)。m×n矩陣的1-范數(shù)條件數(shù)的值為

K₁（A）=‖A‖₁‖A^-1‖₁

其中，1-范數(shù)是矩陣的最大絕對列之和，由以下公式計(jì)算得出：

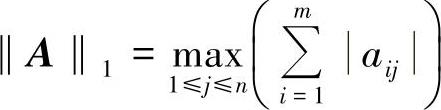
在MATLAB中，condest命令用來求解矩陣的1-范數(shù)條件數(shù)，它的使用格式見表3-7。

表3-7 condest命令的使用格式

例3-12：求矩陣的范數(shù)條件數(shù)。

解：MATLAB程序如下。

1.矩陣條件數(shù)倒數(shù)

在MATLAB中，rcond命令用來求解矩陣的條件數(shù)，它的使用格式見表3-8。

表3-8 rcond命令的使用格式

例3-13：求矩陣的范數(shù)條件數(shù)倒數(shù)

解：MATLAB程序如下。

2.矩陣條件數(shù)

與rcond相比，cond作為估計(jì)矩陣條件的方法更有效，但不太穩(wěn)定。矩陣和計(jì)算任務(wù)的條件數(shù)用于衡量解算過程中答案對輸入數(shù)據(jù)變化和舍入誤差的敏感程度。

矩陣的逆運(yùn)算的條件數(shù)用于測量線性方程組的解對數(shù)據(jù)錯(cuò)誤的敏感程度。它指示矩陣求逆結(jié)果和線性方程解的精度。

在MATLAB中，cond命令用來求解逆矩陣的條件數(shù)，它的使用格式見表3-9。

表3-9 cond命令的使用格式

例3-14：求矩陣的條件數(shù)。

解：MATLAB程序如下。

此矩陣的條件數(shù)不是太大，因此矩陣對逆運(yùn)算不是特別敏感。