1.4.1 現代金融理論基礎
智能金融的特點是以人工智能、大數據、云計算等信息技術為支撐,更加方便快捷、智能有效地提供金融產品和服務。在智能選擇資產組合、根據投資者特點匹配資產組合時離不開金融理論作為基礎。
1.4.1.1 現代資產組合理論
現代資產組合理論(Modern Portfolio Theory, MPT),也稱為現代證券投資組合理論、投資組合理論、證券組合理論或投資分散理論。現代資產組合理論有狹義和廣義之分:狹義的現代資產組合理論指的是馬科維茨的投資組合理論;而廣義的現代資產組合理論除了經典的投資組合理論以及該理論的擴展理論外,還包括由資本資產定價模型和證券市場的有效市場理論構成的資本市場理論。
(1)馬科維茨投資組合理論及拓展
美國經濟學家哈里·馬科維茨(Markowits)于1952年首次提出和創(chuàng)立投資組合理論(Portfolio Theory),并將概率論和線性代數的方法應用于證券投資組合的研究中,進而闡述投資者對于投資活動所最關注的問題是預期收益和預期風險的關系,主要是針對化解投資風險的可能性,“不要把所有的雞蛋放在一個籃子里”就是多元化投資組合的最佳比喻。
該理論包含了兩個重要內容:“均值—方差”分析方法和投資組合有效邊界模型。“均值—方差”分析方法是指用均值和方差來衡量不確定情況下的投資收益和風險。均值是指投資組合的期望收益率,是以投資比例為權重的證券期望收益率的加權平均值,用來衡量投資收益。方差是指投資組合收益率的方差,被稱為波動率的標準差用來衡量投資風險;投資組合有效邊界模型是指最佳投資組合應當是具有風險厭惡特征的投資者的無差異曲線和資產的有效邊界線的交點。
馬科維茨的投資組合理論假設:
①市場是有效的,投資者能夠免費并且同時得知市場上多種證券收益和風險的變動及變動原因。
②投資者是風險厭惡的。投資者總是希望財富越多越好,在其他條件相同時,會選擇具有較高預期收益率的資產組合。同時,其他條件相同時,會選擇具有較小標準差的資產組合,如果要承擔較大的風險則必須有較高的預期收益作為補償。
③投資者以期望收益率和方差(或標準差)來評價單個證券或證券組合的收益和風險。
④投資者總是希望持有有效資產組合,即同一風險水平下,選擇收益率較高的資產組合;同一收益率水平下,選擇風險較低的資產組合,等等。
根據資產組合理論,構建一個完整的投資過程一般有投資決策和融資決策兩個步驟,即所謂的分離定理:第一步為投資決策,確定各類投資工具的收益風險特征,建立并確定包含風險資產和無風險資產的最優(yōu)風險資產組合或市場組合;第二步為融資決策,根據自身風險偏好,在資本市場線上選擇一個有無風險資產與市場組合構造的資產組合,該資產組合要求是投資者的效用滿足程度最高,即無差異曲線和資產資本市場線的切點。
(2)資本市場理論
資本市場理論由資本資產定價模型(Capital Asset Pricing Model, CAPM)和有效市場假說(Efficient Markets Hypothesis, EMH)組成,該理論的產生使關于金融問題的分析實現了從定性到定量的轉變,標志著分析金融學走向成熟。
①資本資產定價模型(CAPM),是在馬科維茨投資組合理論的基礎上,由威廉·夏普(William Sharpe)、約翰·林特納(John Lintner)和簡·莫辛(Jan Mossin)分別獨立提出的。威廉·夏普在馬科維茨的基礎上提出了單指數模型,并提出以對角線模式來簡化方差—協(xié)方差矩陣中的非對角線元素。他據此建立了資本資產定價模型(CAPM),指出無風險資產收益率與有效率風險資產組合收益率之間的連線代表了各種風險偏好的投資者組合。根據上述理論,投資者在追求收益和厭惡風險的驅動下,會根據組合風險收益的變化調整資產組合的構成,進而會影響到市場均衡價格的形成。
資本資產定價模型有許多前提性的假設條件,主要包括對市場的完善性和環(huán)境的無摩擦性,在馬科維茨投資組合理論的假設基礎上還包括:投資者可按照相同的無風險利率無限制地借入或貸出資金;每種資產無限可分,在任何一個投資組合里可以含有非整數份的資產;稅收和交易費用可以忽略不計;對于所有投資者來說,投資期限、無風險利率都相同;所有投資者具有相同的預期,即對各種資產的預期收益率、標準差和資產之間的協(xié)方差具有相同的預期值,等等。
資本資產定價模型指出,由風險資產構成的資產組合的總風險只與各項資產與市場組合的風險相關性(各項資產的收益率與市場組合收益率之間的協(xié)方差)有關,與各項資產本身的風險(各項資產的收益率的方差)無關。也就是說,在投資者心中,如果σiM越大,則第i項資產對市場組合的風險的影響越大,在市場均衡時,應該得到的風險補償就越大。于是得出以下的證券市場線(SML-Security Market Line)公式:
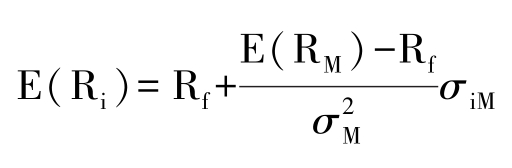
當資本市場達到均衡時,風險的邊際價格是不變的,任何改變市場組合的投資所帶來的邊際效果是相同的,即增加一個單位的風險所得到的補償是相同的。根據Beta系數的定義,可以得到資本資產定價模型:
E(Ri)=Rf+βiM[E(RM)-Rf]
根據資本資產定價模型,我們可以發(fā)現:單個證券的期望收益率由兩個部分組成,無風險利率以及對所承擔風險的補償(風險溢價);風險溢價的大小取決于β值的大小;β值越高,表明單個證券的風險越高,所得到的補償也就越高;β度量單個證券的系統(tǒng)風險,非系統(tǒng)性風險沒有風險補償。
資本資產定價模型主要應用于資產估值、資產配置、評估經營業(yè)績以及資金成本預算等方面。其中,在資產估值方面,資本資產定價模型通過比較均衡的期初價格和實際市場價格,進而判斷證券是否被市場錯誤定價;在資產配置方面,根據對市場走勢的預測,投資者利用資本資產定價模型來選擇具有不同β系數的證券或組合以獲得較高收益或規(guī)避市場風險;在評估經營業(yè)績方面,投資基金實際運作中,經理人員往往只經營熟悉的若干種有價證券,而不是經營一個市場組合。因此,證券市場線可以用來評估他們的經營業(yè)績。
②有效市場假說(Efficient Markets Hypothesis, EMH),始于1965年美國芝加哥大學教授尤金·法瑪發(fā)表的《證券市場價格行為》的論文,并由尤金·法瑪(Eugene Fama)于1970年深化并提出的。
法瑪認為,在資本市場上,如果證券價格能夠充分而準確地反映全部相關信息,便稱其為有效率。也就是說,如果證券價格不會因為向所有的證券市場參加者公開了有關信息而受到影響,那么,就說市場對信息的反映是有效率的。對信息反映有效率意味著以該信息為基礎的證券交易不可能獲取超常利潤。有效市場理論實際上涉及兩個關鍵問題:一是關于信息和證券價格之間的關系,即信息的變化會如何影響價格的變動;二是不同的信息(種類)會對證券價格產生怎樣的不同影響。法瑪還定義了與證券價格相關的三種類型的信息:第一種是“歷史信息”,即基于證券市場交易的有關歷史資料,如歷史股價、成交量等;第二種是“公開信息”,即一切可公開獲得的有關公司財務及其發(fā)展前景等方面的信息;第三種是“內部信息”,即只有公司內部人員才能獲得的有關信息。
1967年5月,在芝加哥大學舉行的證券價格研討會上,哈里·羅伯茨(Harry Roberts)提出了與不同信息相對應的三種不同效率的證券市場理論:
第一種是弱式有效市場理論(Weak Form Efficiency),是指證券價格能夠充分反映價格歷史序列中包含的所有信息,如有關證券的價格、交易量、融資金額等。在弱式有效市場中,股票價格的技術分析失去作用,基本分析還可能幫助投資者獲得超額利潤。
第二種是半強式有效市場理論(Semi-Strong Form Efficiency),是指證券價格不僅能夠體現歷史的價格信息,而且反映了所有與公司證券有關的公開有效信息,如公司收益、股息紅利、對公司的預期、股票分拆、公司間的并購活動等。在半強式有效市場中利用技術分析和基本分析都失去作用,內幕消息可能獲得超額利潤。
第三種是強式有效市場理論(Strong Form Efficiency),是指有關證券的所有相關信息,包括公開發(fā)布的信息和內部信息對證券價格變動都沒有任何影響,即如果證券價格已經充分、及時地反映了所有有關的公開和內部信息,則證券市場就達到了強有效市場。在強式有效市場中,除非存在市場操作,否則沒有任何方法能幫助投資者獲得超額利潤,即使基金和有內幕消息者也一樣。
1.4.1.2 傳統(tǒng)金融定價理論
定價理論是金融學中最核心的理論之一,它試圖解釋確定條件下或不確定條件下未來支付的資產價格或者價值,這里資產通常是指金融工具或某種證券,而價格是其市場均衡時的價格,即由市場需求與供給決定的價格。常見的資產定價理論有無套利定價理論、風險中性定價理論和期權定價理論等。
(1)無套利定價理論
無套利定價理論(Non-arbitrage Pricing Principle)是金融產品定價中常用的分析理論之一。其基本思想是:金融產品在市場上的合理價格就是使得市場不存在無風險套利機會的價格。也就是說,若存在某種證券組合,其初始凈投資為零且收益為正值,那么所有的投資者都會投資該證券組合,進而導致該證券組合的價格發(fā)生變化,直到均衡狀態(tài)下收益降為零,交易不再進行。此時,該資產組合失去了套利的機會,并保持在與資本資產定價模型結果類似的均衡價格,即有效市場上,不存在無風險套利機會。即使存在套利機會,也是暫時的,投資者很快實施套利而使得市場又回到無套利機會的均衡狀態(tài)。
無風險套利機會存在可以等價于以下三種表述條件:①存在兩個不同的資產組合,未來損益相同,但當前價格(成本)不同;②存在兩個當前價格(成本)相同的資產組合,但第一個組合在所有狀態(tài)下的損益都不低于第二個組合的損益。并且,至少存在一種狀態(tài)使得第一個組合的損益大于第二個組合的損益;③一個組合構建成本為零,但在所有狀態(tài)下該組合的損益都不小于零。并且,至少存在一種狀態(tài)使得該組合的損益大于零。簡單來說,無套利定價原理可以理解為相同損益必須相同價格。
無套利定價原理的首要原則是假設套利活動可以在無風險的狀態(tài)下進行,初始投資為零的自融資組合,即投資開始時套利者不需要投入任何資金,投資過程中不需要任何維持成本,卻在未來可以得到正的收益。無套利定價的關鍵技術在于用一組證券來復制另一組證券,即通過構建一個金融工具組合使之與被復制的金融工具具有相同或相似的盈虧狀況。復制可以從正反兩個方面來做:復制未來的現金流,同時檢查目前是否有價格失衡的套利機會;現在的價格相等,復制未來在任何情況下都產生更為有利的現金流,或者未來任何情況下都產生更為不利的現金流。值得注意的是,無論是更為有利還是更為不利都會產生套利機會,但必須是在任何情況下。
無套利定價原理的應用很廣泛,靜態(tài)組合復制定價可以用在確定狀態(tài)下的資產定價,動態(tài)組合復制策略可以進行不確定狀態(tài)的資產定價,以及債券、股票和期權等多種金融產品的定價,且簡單易懂。
(2)風險中性定價理論
風險中性理論(Risk Neutral Pricing Theory),又稱風險中性定價方法,是約翰·考克斯(John Carrington Cox)和斯蒂芬·羅斯(Stephen A. Ross)于1976年推導期權定價公式時建立的。無套利均衡分析方法不涉及投資者的風險偏好,因此適用于風險中性假設的分析方法。
風險中性定價理論是利用風險中性假設的分析方法進行金融產品的定價,即在對衍生證券定價時,假設所有的投資者都是風險中性的,投資過程與投資者的風險偏好無關。此時,所有證券的預期收益率都相同且等于無風險利率r,所有的現金流量都可以通過無風險利率r進行貼現求得現值。該理論的核心在于構造出風險中性概率,進而求出金融衍生品的價值。
例如,一種不支付紅利的股票目前市場價格為S元,已知T時間后,該股票價格要么是Su元,要么是Sd元。假設目前的無風險年利率等于r,現在求一份到期期限為T協(xié)議價格為C元的該股票歐式看漲期權的價值f。
基于風險中性假設,我們可以假設該股票價格上升的概率為p,下跌的概率為1-p,根據股票目前的市場價格,可以列出公式求出風險中性概率p:
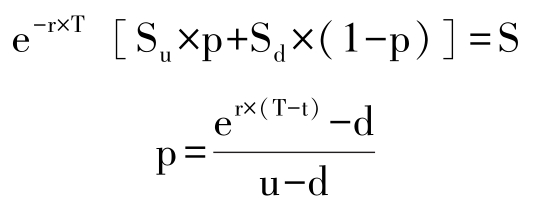
其中,u=1+股票價格上漲狀態(tài)的收益率,d=1+股票下跌狀態(tài)的收益率。求出風險中性概率p后,根據風險中性定價原理,進而可以求出該期權的價值f:
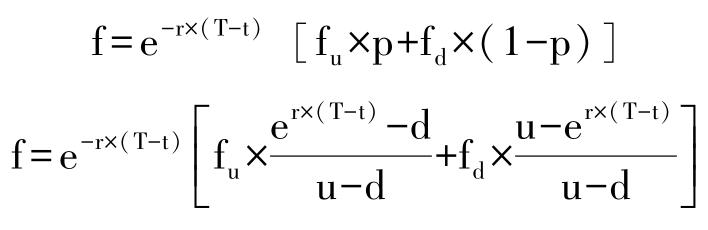
風險中性理論表述了資本市場中的這樣一個結論:在市場不存在任何套利可能性的條件下,如果衍生證券的價格依然依賴于可交易的基礎證券,那么這個衍生證券的價格與投資者的風險態(tài)度無關。
由于風險中性定價原理與投資者的風險態(tài)度無關,從而推廣到對任何衍生證券都適用,所以在以后的衍生證券的定價推導中,都接受了這樣的前提條件,就是所有投資者都是風險中性的,或者是在一個風險中性的經濟環(huán)境中決定價格,并且這個價格的決定,又是適用于任何一種風險態(tài)度的投資者。并且,利用風險中性假設大大簡化了問題的分析,所有資產的均衡定價都可以按照風險中性概率算出未來收益的預期值,再以無風險利率折現得到。最后,將所得的結果放回真實的世界,就會獲得有實際意義的結果。
(3)期權定價理論
期權定價理論(Option Pricing Theory, OPT),也稱布萊克—肖爾斯(Black-Scholes)期權定價理論,簡稱B-S模型,是1973年美國學者布萊克(Fischer Black)和美國學者肖爾斯(Myron Scholes)共同提出的,用于確定歐式股票期權價格,在學術界和實務界引起了強烈反響。同年,默頓(Robert C. Merton)獨立地提出了一個更為一般化的模型。
B-S期權定價理論有一系列的假設條件,主要有:①市場具有無摩擦性,沒有交易成本和稅收,所有資產可以無限細分,沒有賣空的限制;②在期權有效期,可以用相同且不變的利率借貸,利率按照連續(xù)復利r計算;③從時刻t=0到t=T,股票不分紅;④股票價格的變化遵循對數正態(tài)分布的隨機過程,包括以下條件:股票價格連續(xù)變化;整個期權生命期內股票的預期收益和收益方差保持不變;任何時間段股票和其他時間段股票的收益相互獨立,且任何時間段股票的福利收益率服從正態(tài)分布;⑤原始模型定價的是歐式期權,即必須至到期日才能執(zhí)行。
基于以上的假設條件,股票價格的運動遵循一種稱之為帶漂移的幾何布朗運動的規(guī)律,在數學上則表現為被稱作伊藤過程的一種隨機過程,可以表示為:
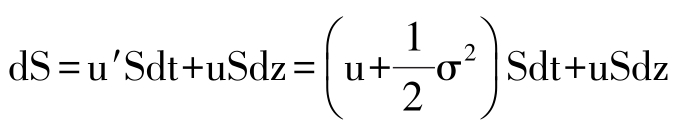
式中:
S是標的物(股票)的價格;
u′是所謂的漂移率,是連續(xù)計算收益率的股票在單位時間內收益的預期收益率, ,u為連續(xù)計算收益率的股票在單位時間內收益的自然對數的數學期望值;
,u為連續(xù)計算收益率的股票在單位時間內收益的自然對數的數學期望值;
σ為波動率,是連續(xù)計算收益率的股票在單位時間內收益的自然對數的標準差;
dz是被稱為維納過程(即布朗運動)的一種隨機過程, ,ε滿足標準正態(tài)分布,數學期望值為0,方差為1。
,ε滿足標準正態(tài)分布,數學期望值為0,方差為1。
基于伊藤引理,經過一系列的推導過程,可以得到B-S隨機微分方程:
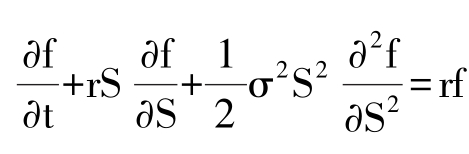
其中,f為衍生證券的價格,S為標的資產的價格,r為無風險利率。B-S隨機微分方程刻畫了動態(tài)調整組合頭寸保持無套利均衡的規(guī)律,適用于其價格取決于標的證券價格S的所有衍生證券的定價。
對于買權來說,有C=f(T)=max[S(T)-X, 0];對于賣權來說,有P=f(T)=max[X-S(T),0]。其中,X為期權中預先確定的標的物的價格,即執(zhí)行價格。根據終端條件,可以倒向接觸B-S隨機微分方程的初始值的表達式,即得出布萊克—肖爾斯期權定價的公式:
C=S(t)N(d1)-Xe-r(T-t)N(d2)
P=Xe-r(T-t)N(-d2)-S(t)N(-d1)
其中,N(·)為累積正態(tài)分布函數,而d ,
, 。應當說明兩點:第一,該模型中無風險利率必須是連續(xù)復利形式;第二,期權有效期T要用相對數表示,即期權有效天數與一年365天的比值。
。應當說明兩點:第一,該模型中無風險利率必須是連續(xù)復利形式;第二,期權有效期T要用相對數表示,即期權有效天數與一年365天的比值。
B-S模型自從1973年首次被提出之后,很快就被芝加哥期權交易所程序化并輸入計算機中加以運用,該公式的應用隨著計算機、通信技術的進步而擴展。如今,B-S期權定價模型以及它的一些變形已被期權交易商、投資銀行、金融管理者、保險人等廣泛應用于證券、期權等金融產品的定價、信用風險的評估和規(guī)避中,對金融產品及金融衍生品的定價、風險規(guī)避和配置具有重要意義。
1.4.1.3 行為金融學理論
現代金融理論是建立在資本資產定價模型(CAPM)和有效市場假說(EMH)兩大基石上的。這些經典理論被局限在理性預期、風險厭惡和有效市場競爭等“理性”的分析框架中,忽視了對投資者實際決策行為的分析。實際情況中,投資者并非完全理性,也有風險厭惡、風險中性和風險偏好等不同的風險態(tài)度。隨著金融產品和市場的發(fā)展,模型和實際的背離使得現代金融理論的理性分析范式陷入了尷尬境地。在此基礎上,20世紀80年代行為金融理論悄然興起,使資本資產定價模型和有效市場假說的權威地位開始動搖。
(1)行為金融學的發(fā)展歷程
行為金融學的早期階段可追溯到19世紀的古斯塔夫·勒龐的《烏合之眾》(The Crowd)和查爾斯·麥基的《大眾幻想與全民癲狂》(Extraordinary Popular Delusion and the Madness of Crowds),這兩本書是研究市場群體行為的經典之作;1936年,凱恩斯最早強調心理預期在投資決策中的作用,并且基于心理預期提出股票投資的選美理論和空中樓閣理論;1951年,普萊爾開拓了應用實驗將投資模型與人的心理行為特征相結合的金融新領域,成為現代意義上行為金融理論的最早研究者。
行為金融學的心理學行為金融階段是指20世紀60年代到80年代中期,以特沃斯基和卡尼曼為代表提出的理論和學說。特沃斯基研究了人類行為與投資決策模型基本假設相沖突的三個方面:風險態(tài)度、心理會計和過度自信,并將觀察到的現象稱為“認知偏差”。特沃斯基和卡尼曼在1979年共同提出的“期望理論”后來發(fā)展成為行為金融研究中的代表學說。但是,對行為金融學的研究在這一時期還沒有引起足夠的重視,人們普遍認為用心理、情緒等主觀因素研究金融行為是不科學的。
行為金融學的金融學行為金融階段是指從20世紀80年代中期至今,由于實際現象和現代金融理論的偏差、期望理論被廣泛認可和應用,行為金融學在這一時期取得了突破性的進展。投資者心理賬戶、股市“羊群效應”、投機價格和流行心態(tài)等觀點注重把心理學研究和投資決策相結合,也從投資策略上完善了對行為金融理論的研究。
(2)行為金融學的主要內容
①期望理論
期望理論(Prospect Theory)是1979年由特沃斯基和卡尼曼共同提出來的,是行為金融學的重要理論基礎。他們在研究不確定的條件下人們如何做出決策的過程中,發(fā)現大多數投資者并非標準金融投資者而是行為投資者,他們的行為不總是理性的,也并不總是風險回避的。
期望理論中最為人們熟知的經典斷論:
一是決策效應。決策效應是以確定性效應為基礎表明了個體對風險的態(tài)度,認為與一個預期收入更大的不確定選擇相比,人們更愿意一個收入確定的選擇;與一個預期損失確定的選擇相比,人們更愿意一個預期損失更大的不確定選擇,即絕大多數投資者對不確定結果中增益的結果持厭惡回避態(tài)度,對確定性結果中損失的結果持追逐風險的狀態(tài)。
二是價值函數。價值是由財富的變化決定的而不是個體的最終財富。也就是說,在不確定的條件下,人們的投資偏好是由財富的增量決定,而不是財富總量決定,人們對于損失的敏感度要高于收益。投資者對收益的效用函數是凹函數,對損失的效用函數是凸函數。即人們在盈利的情況下表現為風險厭惡者,在已經損失的情況下標簽為風險追求者。
期望理論成為行為金融研究中的代表學說,解釋了不少金融市場中的異常現象:如阿萊悖論、股價溢價之謎和波動率微笑等,然而特沃斯基和卡尼曼在期望理論中并沒有給出如何確定價值函數的關鍵——參考點以及價值函數的具體形式,在理論上存在很大缺陷,從而極大阻礙了期望理論的進一步發(fā)展。
②套利限制
套利限制是行為金融學對傳統(tǒng)金融理論提出質疑和修正的重要工具。傳統(tǒng)金融理論的一個重要理論基礎為有效市場假說。即資產的價格能夠反映與資產相關的一切信息,價格和價值是一致的。理性的交易者能夠正確評估證券的價格。如果存在很多非理性交易者,那么,一方面,如果非理性交易者的非理性行為相互抵消,則對市場的有效性沒有影響;另一方面,如果非理性交易者的非理性方向是相同的,這時候由于套利的存在,短期內的價格偏離很快也會得到糾正,從而使市場能夠恢復效率。
但是,行為金融學認為套利不可能不受條件限制,如套利的執(zhí)行成本或模型風險。在各種客觀約束下,套利無法剔除非理性行為對理性行為的長期并且是實質性的影響,所以有效市場假說是不成立的,即“套利限制”。
③其他理論
過度自信是指不論是理性行為者還是非理性行為者,都不會懷疑自己的理性的存在。他們自認為掌握了一定信息和一定專業(yè)知識,因而面對投資決策的時候,過于相信自己的判斷力,往往高估他們的投資決策盈利的概率。
易獲得性偏誤是指某件事情比較容易被想到,投資者便誤認為這個事件經常發(fā)生;相反,如果某類事件不太容易被想象到,投資者就會在不自覺的情況下低估該類事件發(fā)生的概率。因此,投資者在決策時受社會化影響的程度是不可忽視的。例如,把經濟泡沫和房地產相聯(lián)系,由股市不景氣聯(lián)想到互聯(lián)網在走下坡路等。
心理賬戶是指投資人的投資決策實際上是不確定條件下的心理選擇。特沃斯基和卡尼曼在預期財富和財富低于可以維持的概率的情況下描繪了行為組合理論的有效邊界。行為組合理論包括單一心理賬戶和多個心理賬戶,其中單一心理賬戶投資者關心投資組合中各資產的相關系數,所以他們會將投資組合整個放在一個心理賬戶中,而多個心理賬戶投資者會將投資組合分成不同的賬戶,忽視各個賬戶之間的相互關系。
許多行為金融學學者都認為,在投資者進行決策的時候,并不是權衡了全局的各種情況,而是在心里無意識地把一項決策分成幾個部分來看,也就是說,分成了幾個心理賬戶,對于每個心理賬戶行為者會有不同的決策。與現代資產組合理論認為投資者最優(yōu)的投資組合應該在均值方差的有效前沿上不同的是,行為組合理論實際構建的資產組合是基于對不同資產的風險程度的認識以及投資目的所形成的一種金字塔式的資產組合。金字塔的每一層都對應著投資者特定的投資目的和風險特征。投資者通過綜合考察現有財富、投資的安全性、期望財富水平、達到期望水平的概率等幾個因素來選擇符合個人愿望的最優(yōu)投資組合。
特沃斯基和卡尼曼認為普通投資者會將自己的投資組合分成兩部分:一部分是風險低的安全投資;另一部分是風險較高但可能使自己更富有的投資。這是由于人們都有既想避免損失又想變得富有的心態(tài),因此,人們會把兩個心理賬戶分開來,一個用來規(guī)避貧窮,另一個用來一朝致富。而且,在考慮問題的時候,投資者往往每次只考慮一個心理賬戶,把目前要決策的問題和其他的決策分離看待。也就是說,投資人可能將投資組合放在若干個心理賬戶中,不太在意它們之間的共同變異數,這也就從另一個角度解釋了投資者在有些情況下的非理性行為。
總之,行為金融理論在博弈論和實驗經濟學被主流經濟學接納之際,對人類個體和群體行為研究的日益重視,將投資者的感情因素、心理活動、社會規(guī)范和觀念習慣等因素考慮到投資決策的過程中,將人類心理與行為納入金融的研究框架,但是由于涉及人類心理與行為研究的難度,加上行為金融學剛剛起步還不完善,因而其本身也存在很多缺陷,還有待進一步發(fā)展和完善。