- Supervised Machine Learning with Python
- Taylor Smith
- 155字
- 2021-06-24 14:01:06
Measuring the slope of multiple functions
We want to get really complicated, though, and measure the slopes of multiple functions at the same time. All we'll end up with is a matrix of gradients along the rows. In the following formula, we can see the solution that we just solved from the previous example:

In the next formula, we have introduced this new function, called g. We see the gradient for function g, with each position corresponding to the partial derivative with respect to the variables x and y:

When we stack these together into a matrix, what we get is a Jacobian. You don't need to solve this, but you should understand that what we're doing is taking the slope of a multi-dimensional surface. You can treat it as a bit of a black box as long as you understand that. This is exactly how we're computing the gradient and the Jacobian:
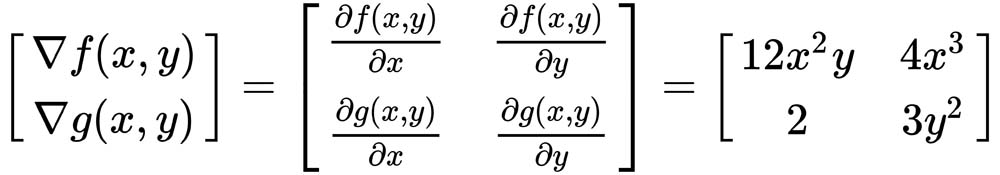
- Hands-On Internet of Things with MQTT
- Dreamweaver CS3網頁制作融會貫通
- MCSA Windows Server 2016 Certification Guide:Exam 70-741
- UTM(統一威脅管理)技術概論
- 塊數據5.0:數據社會學的理論與方法
- ESP8266 Home Automation Projects
- OpenStack Cloud Computing Cookbook
- 突破,Objective-C開發速學手冊
- 網絡安全技術及應用
- LMMS:A Complete Guide to Dance Music Production Beginner's Guide
- 計算機組成與操作系統
- 網絡存儲·數據備份與還原
- 嵌入式Linux系統實用開發
- 網絡信息安全項目教程
- Hands-On Microservices with C#