- Supervised Machine Learning with Python
- Taylor Smith
- 175字
- 2021-06-24 14:01:05
Measuring the slope of a curve
The following is a quick refresher on scalar derivatives. To compute the slope at any given point, the standard way is to typically measure the slope of the line between the point we're interested in and some secant point, which we'll call delta x:
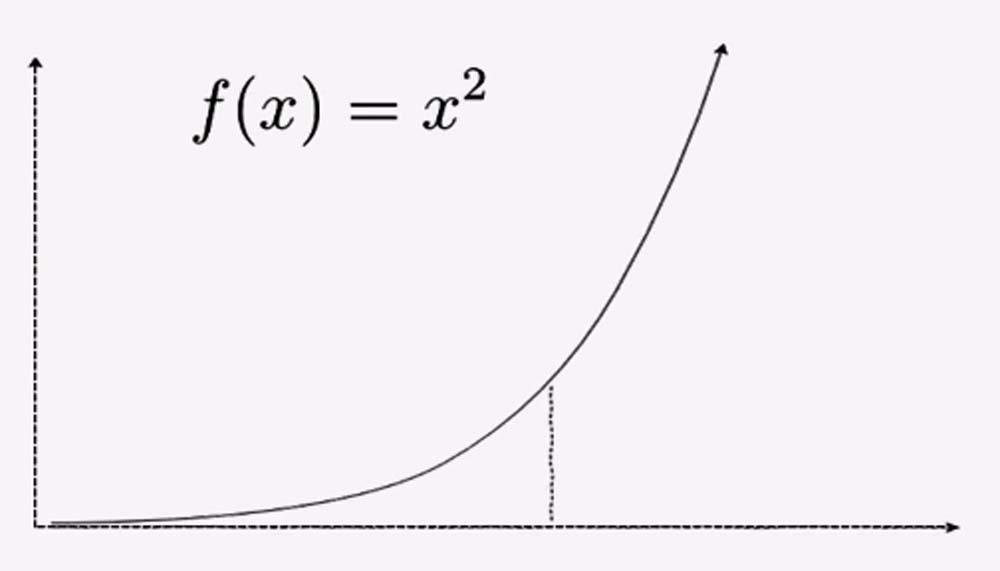
As the distance between x and its neighbor delta x approaches 0, or as our limit approaches 0, we arrive at the slope of the curve. This is given by the following formula:
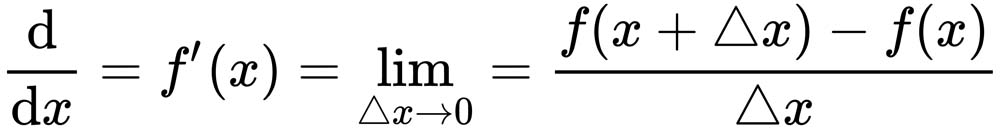
There are several different notations that you may be familiar with. One is f prime of x. The slope of a constant is 0. So, if f(x) is 9, in other words, if y is simply 9, it never changes. There is no slope. So, the slope is 0, as shown:
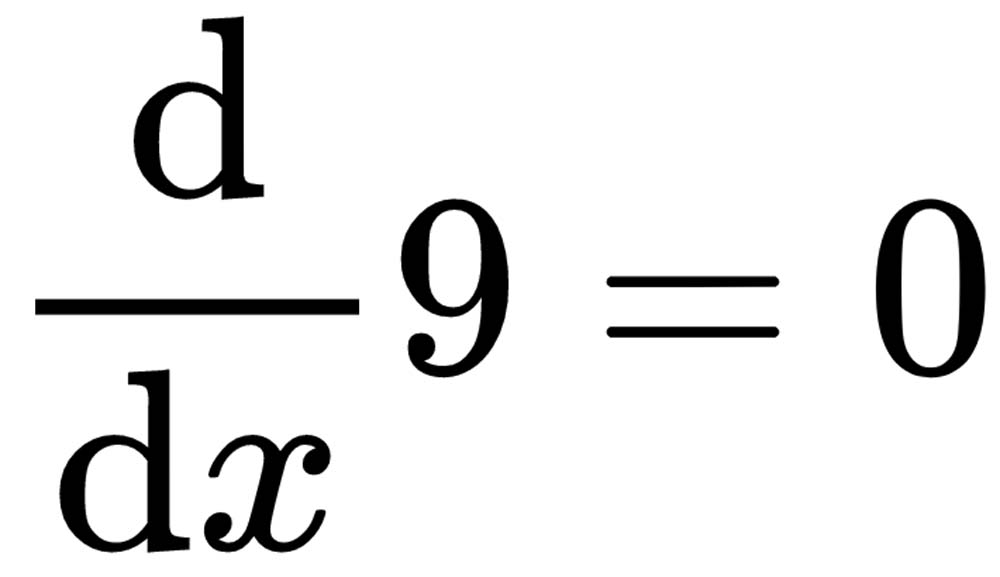
We can also see the power law in effect here in the second example. This will come in useful later on. If we multiply the variable by the power, and decrement the power by one, we get the following:
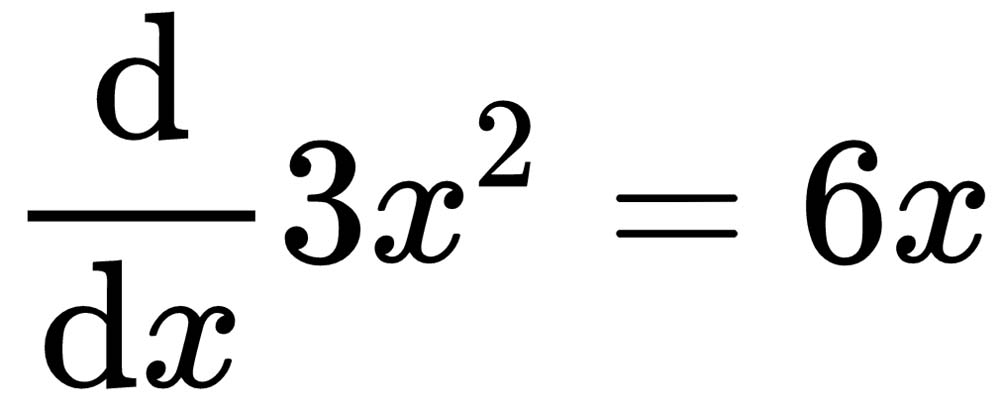
- Google Cloud Platform Cookbook
- 嵌入式Linux上的C語言編程實踐
- 大數(shù)據(jù)安全與隱私保護(hù)
- Photoshop CS3特效處理融會貫通
- 大學(xué)計算機(jī)應(yīng)用基礎(chǔ)
- 高維聚類知識發(fā)現(xiàn)關(guān)鍵技術(shù)研究及應(yīng)用
- 我也能做CTO之程序員職業(yè)規(guī)劃
- 突破,Objective-C開發(fā)速學(xué)手冊
- 網(wǎng)站前臺設(shè)計綜合實訓(xùn)
- 筆記本電腦維修90個精選實例
- 從零開始學(xué)SQL Server
- 學(xué)練一本通:51單片機(jī)應(yīng)用技術(shù)
- Silverlight 2完美征程
- MATLAB-Simulink系統(tǒng)仿真超級學(xué)習(xí)手冊
- 網(wǎng)絡(luò)脆弱性掃描產(chǎn)品原理及應(yīng)用