- 數據結構案例教程(C/C++版)
- 于泠 陳波編著
- 751字
- 2020-10-23 14:23:40
1. 2 知識應用
本節運用1. 1節所學知識來分析導學問題1中涉及的數據結構以及計算導學問題2的時間復雜度。
1.2.1 導學問題1-4、1-5和1-6的數據結構
對于導學問題1-4、1-5和1-6這幾個比較復雜的問題,先對其抽象出數學模型。
如圖1-11所示,在問題1-4中的學生成績表中,每個學生的學號、姓名、某門課程的成績稱為數據項,每個學生包含這些數據項的記錄稱為數據元素。所有數據元素(這個班級的學生)的集合就構成了一個數據對象。
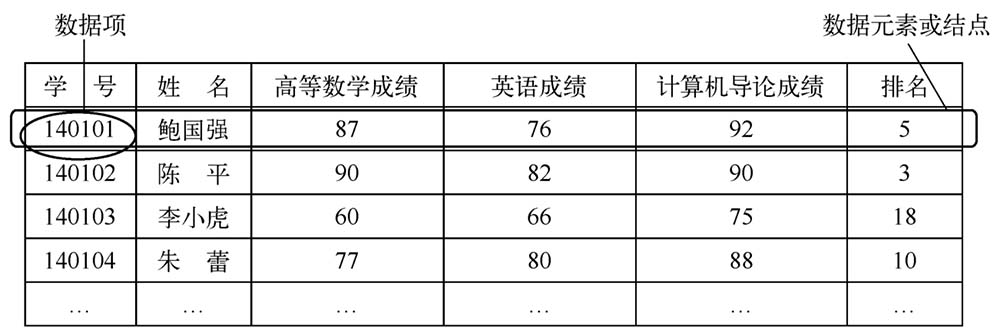
圖1-11 學生成績表中的數據項、數據元素
將每一個數據元素看作一個結點,用圓圈表示,元素之間的邏輯關系用結點之間的連線表示,則問題就可以抽象成如圖1-12所示的一對一的線性邏輯結構。

圖1-12 線性邏輯結構
在問題1-5中,把Linux系統中的文件、文件夾稱為數據元素,將每一個數據元素看作一個結點,用圓圈表示,元素之間的邏輯關系用結點之間的連線表示,則問題中的數據元素之間的關系就可以抽象成如圖1-13所示的樹形邏輯結構。本書將在第6章介紹“樹”這種抽象結構的存儲和操作實現。
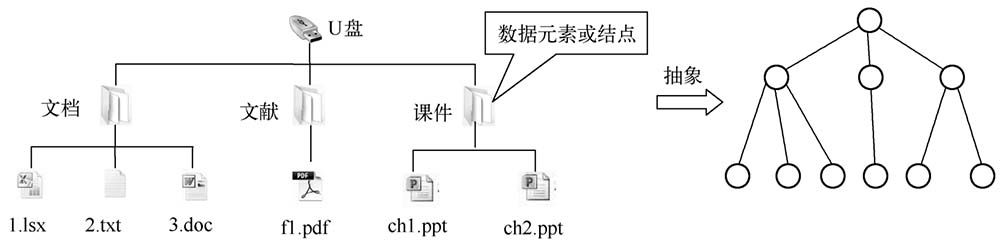
圖1-13 樹結構
在問題1-6中,數據元素之間的關系可以抽象成如圖1-14所示的圖結構。本書將在第7章介紹“圖”這種抽象結構的存儲和操作實現。
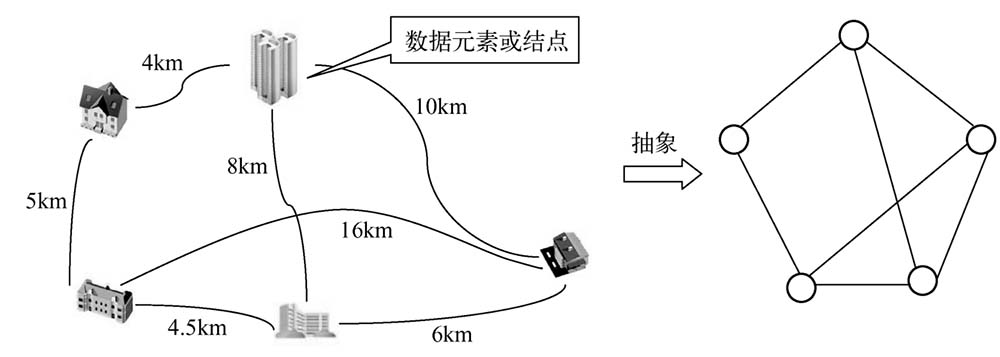
圖1-14 圖結構
1.2.2 導學問題2的時間復雜度
由于循環語句的執行時間主要取決于循環體執行的次數,因此在分析循環語句時間復雜度時,更多關注的是循環體中基本語句執行的次數。
導學問題2的原始程序是一個雙重循環,其中外循環體中的語句p=1,執行次數為n;外循環體中的語句s+=p,執行次數為n;內循環體中語句p*=j,執行次數為1+2+3+…+n=n(n+1)/2;因此該程序的基本語句執行次數是n2數量級,時間復雜度T(n)=O(n2)。
改進后的程序是一個單重循環,循環體中的語句p*=j;和s+=p;分別執行了n次,因此該程序的基本語句執行次數是n數量級,時間復雜度T(n)=O(n)。
顯然,改進后的程序在時間復雜度上要比初始的程序好。
- 多媒體CAI課件設計與制作導論(第二版)
- Java語言程序設計
- Node.js Design Patterns
- Java系統分析與架構設計
- 算法零基礎一本通(Python版)
- Python數據可視化:基于Bokeh的可視化繪圖
- Python從入門到精通(精粹版)
- Julia高性能科學計算(第2版)
- BeagleBone Robotic Projects(Second Edition)
- Using Yocto Project with BeagleBone Black
- MongoDB Cookbook
- 例說FPGA:可直接用于工程項目的第一手經驗
- Apache Solr for Indexing Data
- 編程風格:程序設計與系統構建的藝術(原書第2版)
- INSTANT Apache Maven Starter