- 數據結構:C語言描述(融媒體版)
- 劉小晶
- 7019字
- 2021-04-07 18:10:11
2.2 線性表的順序存儲及其實現
2.2.1 線性表的順序存儲
1.順序表的定義
所謂順序表就是順序存儲的線性表。順序存儲是用一組地址連續的存儲單元依次存放線性表中各個數據元素的存儲結構,如圖2-2所示。

圖2-2 線性表的順序存儲結構
假設線性表的數據元素類型為ElemType,則每個數據元素所占用的存儲空間大小為sizeof(ElemType),長度為n的線性表所占用的存儲空間大小為n×sizeof(ElemType)。
2.順序存儲中數據元素的地址計算公式
因為線性表中所有數據元素的類型是相同的,所以每一個數據元素在存儲器中占用相同大小的空間。假設每一個數據元素占C個存儲單元,且a1的存儲地址為Loc(a1)(線性表的基地址),則根據順序存儲的特點可得出第i個數據元素的地址計算公式為
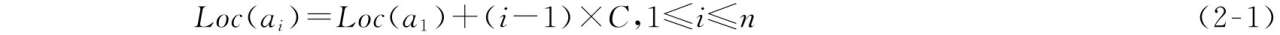
以上表明,只要知道順序表的基地址和每一個數據元素所占存儲空間大小,就可以計算出線性表中任何位序號上的數據元素的存儲地址。由此可知:線性表的順序存儲結構是一種隨機存取的存儲結構。
3.線性表順序存儲的特點
(1)在線性表中,邏輯上相鄰的數據元素,在物理存儲位置上也是相鄰的。
(2)存儲密度高。

在線性表的順序存儲結構中,只要存放數據元素值本身,其數據元素之間的邏輯關系是通過物理上的存儲位置關系來反映的,所以,數據元素的存儲密度為1。
(3)便于隨機存取。在線性表基地址已知的情況下,只要明確數據元素在線性表中的位序號就可由式2-1方便地計算出該元素在順序存儲中的地址。計算機根據地址就可快速對該地址空間中的元素進行讀與寫。
上述特點,可謂是線性表順序存儲的優點,但它也存在不盡如人意的地方:
(1)要預先分配“足夠應用”的存儲空間,這可能會造成存儲空間的浪費,也可能會造成空間不夠實際應用而需要再次請求增加分配空間,從而擴充存儲容量。
(2)不便于插入和刪除操作。這是因為在順序表上進行插入和刪除操作時,為了保證數據元素的邏輯位置關系與存儲位置關系一致,則必然會引起大量數據元素的移動。如圖2-2所示,要在這個順序表中第i個位置前插入一個新元素,則一定要將第i個元素及其之后的所有元素都先往后移一位,使第i個存儲單元騰空后才能將新元素插入。
4.順序存儲結構的描述
高級程序設計語言在程序編譯時會為數組類型的變量分配一片連續的存儲區域,數組元素的值就能依次存儲在這片存儲區域中;其次,數組類型也具有隨機存取的特點。因此,可用數組來描述數據結構中的順序存儲結構,其中數組元素的個數對應于存儲區域的大小,且應根據實際需要定義為“足夠大”,假設為MAXSIZE(符號常量)。考慮到線性表的實際長度是可變的,故還需用一個變量length來記錄線性表的當前長度。下述類型說明就是線性表的靜態順序存儲結構描述。
#defineMAXSIZE 80 //線性表預分配空間的容量
typedef int ElemType; //為方便后續算法的描述,將ElemType類型自定義為int類型
typedef struct {
ElemType elem[MAXSIZE]; //線性表的存儲空間
int Length; //線性表的當前長度
}SqListTp;
根據上述描述,對于線性表L={34,12,25,61,30,49},其順序存儲結構可用圖2-3表示。
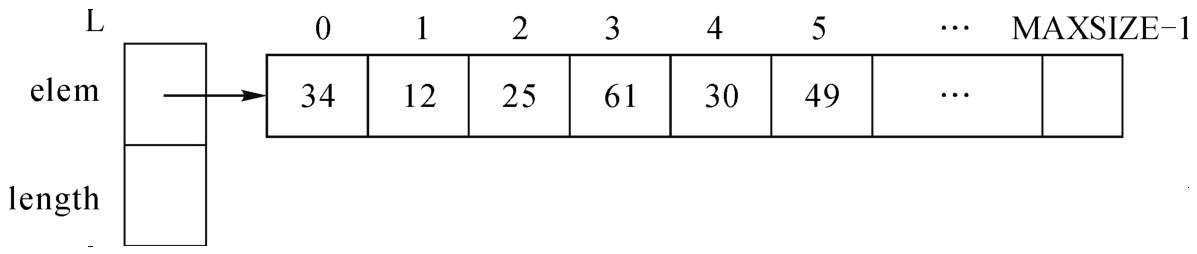
圖2-3 線性表L={34,12,25,61,30,49}的順序存儲結構
由于在C語言中數組空間是在程序編譯時分配的,所以線性表上面描述的順序存儲空間被稱為靜態順序存儲空間。它的容量在程序運行時是不能夠根據需要進行動態增加的,這就不能滿足線性表的長度在實際應用時是動態變化的需求。為此,可以使用動態的順序存儲空間來存儲線性表。下述類型說明就是動態順序存儲結構的描述:

C0 2-2-1
#define LIST_INIT_SIZE 80 //線性表初始分配空間的容量
#define LISTINCREMENT 10 //線性表增加分配空間的量
typedef int ElemType;
typedef struct {
ElemType *elem; //線性表的存儲空間基地址
int length; //線性表的當前長度
int listsize; //線性表當前的存儲空間容量
}SqList;
其中常量LIST_INIT_SIZE設定為線性表初始分配空間的容量,而常量LISTINCREMENT是在線性表需擴充空間時,而設定的增加分配空間的量。與靜態順序存儲結構的描述相比,動態順序存儲結構描述中elem是用來存儲連續存儲空間的基地址,listsize是用來記載當前為線性表分配空間的容量值。開始時它們的值并未確定,只有在程序運行時,當為線性表分配了具體大小的存儲空間后才能確定其值,并且其空間容量在程序運行時也可以根據需要進行動態的增加,從而克服了靜態順序存儲結構的不足。
對于線性表L={a1,a2,…,ai,…,an},其動態順序存儲結構如圖2-4所示。
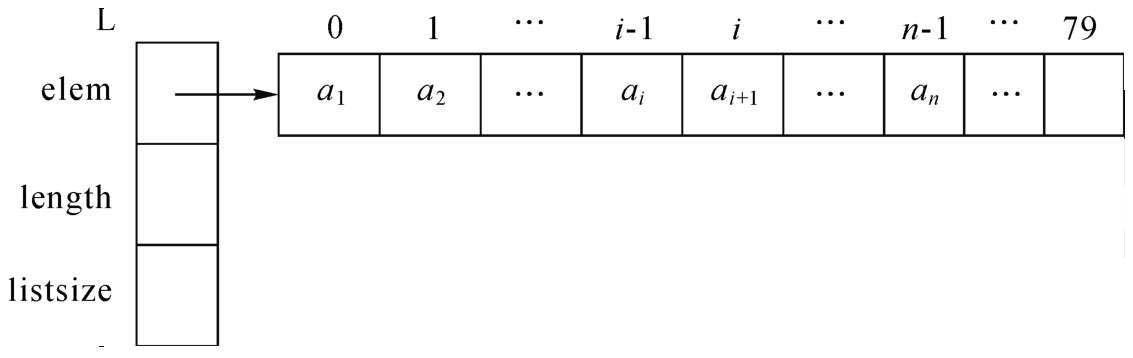
圖2-4 線性表L={a1,a2,…,ai,…,an}的順序存儲結構
特別說明:
(1)本書后面的順序存儲結構全部采用動態順序存儲結構描述。
(2)對于已知如圖2-4所示的順序表L,其存儲空間基地址的直接訪問形式為L.elem;第i個數據元素ai的直接訪問形式為L.elem[i-1](注意元素在表中的位序號與在數組中下標之間的差別);表長的直接訪問形式為L.length;預分配空間容量的直接訪問形式是L.listsize。
2.2.2 順序表上基本操作的實現
從上述線性表的順序存儲結構示意圖或特別說明中的內容可知,對順序表的清空、判空、求長度和取第i個元素的操作都非常容易實現,算法簡單。因此,下面只介紹順序表的初始化、插入、刪除和查找操作的實現算法。
1.順序表的初始化操作
順序表的初始化操作InitList(&L)的基本要求是創建一個空的順序表L,也就是一個長度為0的順序表。其存儲結構如圖2-5所示。要完成此操作的主要步驟可歸納如下:
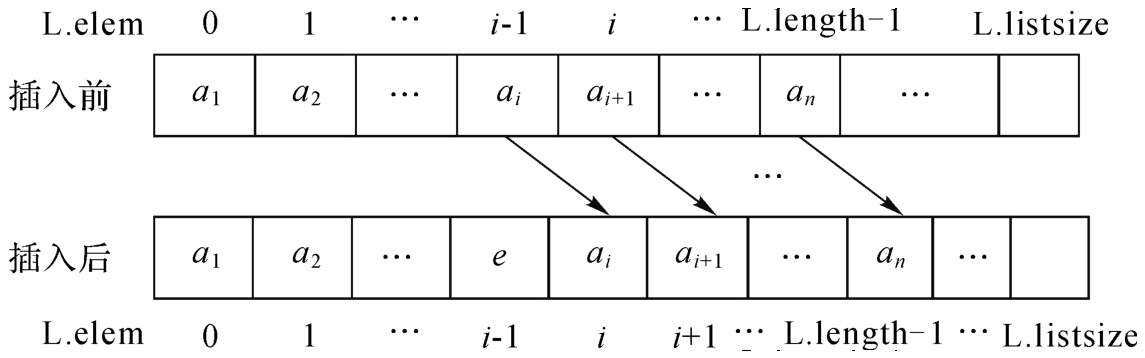
圖2-5 順序表插入前、后的存儲結構狀態
(1)分配預定義大小的數組空間。數組空間用于存放線性表中各數據元素,分配空間可用C語言中的庫函數malloc來實現,空間的大小遵守“足夠應用”的原則,可通過符號常量LIST_INIT_SIZE的值進行預先設定。
(2)如果空間分配成功,則置當前順序表的長度為0,置當前分配的存儲空間容量為預分配空間的大小。
【算法2-4】順序表的初始化操作算法
Status InitList(SqList&L)
//創建一個空的順序表L
//分配預定義大小的存儲空間
{ L.elem=(Elem Type*)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(! L.elem) //如果空間分配失敗
exit(OVERFLOW);
L.length=0; //置當前順序表的長度為 0
L.listsize=LIST_INIT_SIZE; //置當前分配的存儲空間容量為LIST_INIT_SIZE的值
return OK;
}//算法2-4 結束
2.順序表上的插入操作
順序表上進行插入操作ListInsert(&L,i,e)的基本要求是在已知順序表L上的第i個數據元素ai之前插入一個值為e的數據元素,其中1≤i≤L.length+1。當i=1時,在表頭插入e;當i=L.length+1時,在表尾插入e。插入操作后順序表的邏輯結構由原來的(a1,a2,…,ai,ai+1,…,an)變成了(a1,a2,…,ai-1,e,ai,…,an),且表長增加1,如圖2-5所示。
根據順序表的存儲特點,邏輯上相鄰的數據元素在物理上也是相鄰的,要在數據元素ai之前插入一個新的數據元素,則需將第i個數據元素ai及之后所有的數據元素后移一個存儲位置,再將待插入的數據元素插入到騰出的存儲位置上。下面將順序表上的插入操作的主要步驟歸納如下:
(1)插入操作的合法性判斷。在進行插入操作之前需對插入位置i的合法性和存儲空間是否滿進行判斷。若i不合法,即i<1或i>L.length+1,則以操作失敗結束算法;若當前存儲空間已滿,即當前存儲空間中存放數據元素的個數大于或等于當前存儲空間的容量(L.length>=L.listsize)時,則需對線性表的存儲空間進行擴充,擴充后再進行以下操作。
(2)確定插入位置。說明:此操作的插入位置在已知條件中已明確規定是i。若將操作要求改為在有序的順序表中插入一個值為e的數據元素時,則插入位置必須經過一定次數的比較后才能確定。
(3)將插入位置及其之后的所有數據元素后移一個存儲位置。
注意:必須先從最后一個數據元素開始依次逐個進行后移,直到第i個數據元素移動完畢為止。
(4)表長加1。

C0 2-2-2
【算法2-5】順序表的插入操作算法
1 Status ListInsert(SqList&L,int i,ElemType e)
2 //在順序表L的第i個元素之前插入新的元素e,其中 1≤i≤L.length+1
3 { ElemType *newbase,*p,*q;
4 if(i < 1||i > L.length+1) //如果插入位置i不合法
5 return ERROR;
6 if(L.length >=L.listsize) //當前存儲空間已滿,則增加分配以擴充空間
7 { newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
8 if(! newbase) //如果空間分配失敗
9 exit(OVERFLOW);
10 L.elem=newbase; //修改增加空間后的基址
1 1 L.l istsize+=LISTINCREMENT; //修改增加空間后的存儲空間容量
12 }
13 q=&(L.elem[i-1]); //q指示插入位置
14 for(p=&(L.elem[L.length-1]);p>=q;--p)//p始終指示待移動的元素
15 *(p+1)=*p; //插入位置及其之后的所有元素后移一位
1 6 *q=e; //e插入騰空的位置
17 ++L.length; //表長增 1
18 return OK;
19 }//算法2-5 結束
算法2-5與下面的算法2-6實現的功能是等價的。前者在算法中是通過指針來間接訪問到數據元素,而后者在算法中是通過數組元素的訪問形式直接訪問到數據元素,讀者可以根據自己的理解選擇使用。
【算法2-6】順序表的插入操作算法
1 Status ListInsert_1(SqList&L,int i,ElemType e)
2 //在順序表L的第i個數據元素之前插入新的元素e,其中 1≤i≤L.length+1
3 { ElemType *newbase;
4 if(i<1||i>L.length+1) //如果插入位置i不合法
5 return ERROR;
6 if(L.length>=L.listsize) //當前存儲空間已滿,則增加分配以擴充空間
7 {newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
8 if(! newbase) //如果空間分配失敗
9 exit(OVERFLOW);
10 L.elem=newbase; //修改增加空間后的基址
1 1 L.l istsize+=LISTINCREMENT;//修改增加空間后的存儲空間容量
12 }
13 for(int j=L.length-1;j>=i-1;j--)
14 L.elem[j+1]=L.elem[j]; //將插入位置及其之后的所有元素后移一位
15 L.elem[i-1]=e; //e插入騰空的位置
16 L.length++; //表長增 1
1 7 return OK;
18 }//算法2-6 結束
順序表上的插入操作算法,其執行時間主要花費在數據元素的移動上,即算法2-5中的第15行和算法2-6中的第14行語句的執行上,所以此語句的操作是該算法的關鍵操作。若順序表的表長為n,要在順序表的第i(1 ≤i≤n+1)個數據元素之前插入一個新的數據元素,則第15行或第14行語句的執行次數為n-i+1,即會引起n-i+1個數據元素向后移動一個存儲位置,所以算法中數據元素移動的平均次數為

其中:pi是在順序表的第i個存儲位置之前插入數據元素的概率。假設在任何位置上插入數據元素的概率相等,即 ,則式2-2可寫成:
,則式2-2可寫成:
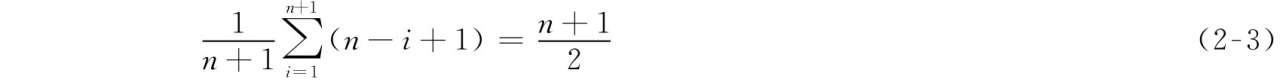
由式2-3可知,算法2-5與算法2-6的時間復雜度為O(n)。
3.順序表上的刪除操作
順序表上的刪除操作ListDelete(&L,i,&e)的基本要求是將已知順序表L上的第i個數據元素ai從順序表中刪除,并用e返回被刪元素的值。其中:1≤i≤L.length。
刪除操作后會使順序表的邏輯結構由原來的(a1,a2,…,ai-1,ai,,ai+1,…,an)變成(a1,a2,…,ai-1,ai+1,…,an),且表長減少1,如圖2-6所示。
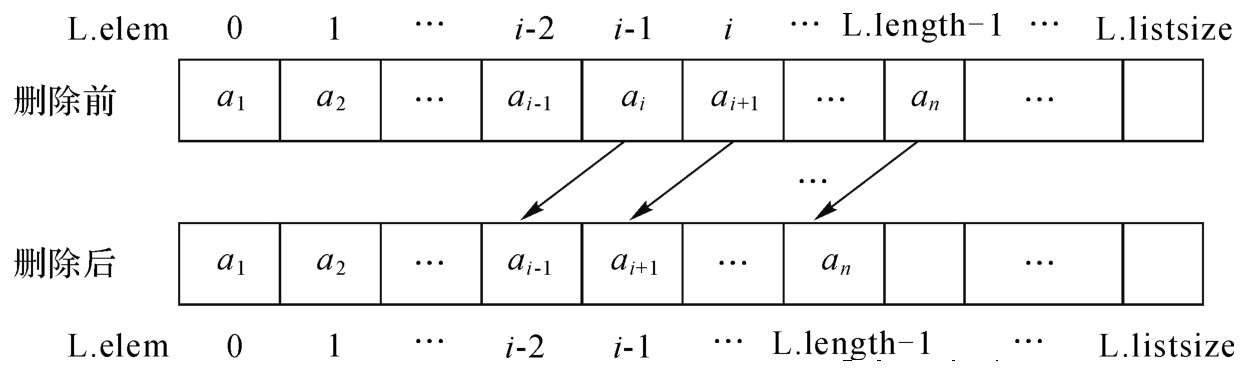
圖2-6 順序表刪除前、后的存儲結構狀態
刪除操作后為保持邏輯上相鄰的數據元素在存儲位置上也相鄰,就要將第i個數據元素ai之后的所有數據元素都向前移動一個存儲位置。下面將順序表上的刪除操作的主要步驟歸納如下:
(1)判斷刪除位置i的合法性,若i不合法,則以操作失敗結束算法。

C0 2-2-3
說明:當1≤i≤L.length時為合法值。
(2)將第i個數據元素之后的所有數據元素向前移動一個存儲位置。
(3)表長減1。
【算法2-7】順序表的刪除操作算法
1 Status ListDelete(SqList&L,int i,ElemType&e)
2 //刪除順序表L中的第i個數據元素,并用e返回其值,其中 1≤i≤L.length
3 { ElemType *p,*q;
4 if((i < 1)||(i > L.length))//如果刪除位置i不合法
5 return ERROR;
6 p=&(L.elem[i-1]); //p先指示被刪除元素的位置
7 e=*p; //被刪除元素的值用e保存
8 q=L.elem+L.length-1; //q指示表尾元素的位置
9 for(++p;p <=q;++p) //p始終指示待移動的元素
1 0 *(p-1)=*p; //將被刪元素之后的所有元素前移一位
1 1 --L.length; //表長減 1
12 return OK;
13 }//算法2-7 結束
注意:讀者也可以按照算法2-6的實現方法來改寫算法2-7,請思考并完成。其實本節中所有的基本操作算法都可以考慮用這兩種方法來實現,下面也都只給出了其中一種實現算法。
在順序表中刪除一個數據元素,其執行時間仍然主要花費在數據元素的移動操作上,也就是算法2-7中第10行的語句的執行上。這里移動的數據元素的個數與插入操作中相似,取決于被刪除元素的起始存儲位置。在長度為n的順序表上刪除第i(1≤i≤n)個數據元素會引起n-i個數據元素發生移動,所以算法中數據元素移動的平均次數為

假設在任何位置上刪除元素的概率相等,即 ,則式2-4可寫成:
,則式2-4可寫成:

由式2-5可知,算法2-7的時間復雜度仍為O(n)。
4 .順序表上的查找操作
查找操作一般有兩種情況:一種是查找指定位置上的數據元素的值;另一種是查找滿足指定條件的數據元素初次出現的位置。前者在順序表的實現簡單,用隨機存取的方式就可找到對應的數據元素,時間復雜度為O(1)。對于后者的查找操作LocateElem(L,e)的基本要求是在順序表L中查找值為e的數據元素初次出現的位置。該操作實現的方法是將e與順序表的每一個數據元素依次進行比較,若經過比較相等,則返回該數據元素在順序表中的位序號,若所有數據元素都與e比較且不相等,表明值為e的數據元素在順序表中不存在,返回0。
【算法2-8】順序表的查找操作算法
1 int LocateElem(SqList L,ElemType e)
2 //查找線性表L中值為e的數據元素,并返回線性表中首次出現指定數據元素e的位序號,若線性
表中不包含此數據元素,則返回 0
3 { int i;
4 for(i=1;i<=L.length&&L.elem[i-1]!=e;i++);
5 if(i<=L.length)
6 return i;
7 else
8 return 0;
9 }//算法2-8 結束
此算法的執行時間主要體現在數據元素的比較操作上,即算法中第5行語句的執行時間,該執行時間取決于值為e的數據元素所在的存儲位置。若順序表中第i(1 ≤i≤n)個位置上的數據元素值為e,則需比較i次;若順序表中不存在值為e數據元素,則需將順序表中所有的數據元素都比較一遍后才能確定,所以需要比較n次。因此,在等概率條件下,數據元素的平均比較次數為

由式2-6可知,算法2-8的時間復雜度為O(n)。
5.順序表的輸出操作
輸出操作DisplayList(L)的基本要求是將數組空間中的每個數據元素值依次輸出。
【算法2-9】順序表的輸出操作算法
void DisplayList(SqList L)
//輸出順序表L中各數據元素值
{ for(int i=0;i<=L.length-1;i++)
printf("%4d",L.elem[i]);
printf("\n");
}
//算法2-9 結束
此算法的時間復雜度為O(n)。
2.2.3 順序表應用舉例
對數據結構最常用的操作就是增、刪、查,但在解決實際問題時,其具體操作的已知條件往往會發生變動,所以讀者在理解順序表上這三種基本操作的實現方法時,一定要抓住其通用性的主要操作步驟和每個步驟的實現方法是什么,這樣才能靈活使用這些通用性的內容方法去解決其他一些實際問題。下面希望通過一些實例來進一步熟悉常用操作的通用性方法的套用。
【例2-4】已知一個有序順序表L,設計一個算法在L中插入一個數據元素值為x的新元素,并使順序表L仍然保持有序。
【分析】本題涉及的知識點是順序表的插入操作。前面已經介紹過:若要在順序表上實現插入操作,如果當前順序表的存儲空間未滿,則主要操作步驟是先確定待插入的位置,再將插入位置及其之后的所有數據元素后移一位,然后將待插入的數據元素插入到空出的位置上,最后表長加1。這些步驟中最關鍵的是如何確定待插入的位置。假設順序表是一種非遞減的有序表,所以要確定待插入的位置可以有兩種實現方法。方法一:從順序表的表頭開始依次往后將數據元素值與x進行比較,當數據元素值比x值小時,則繼續往后進行比較,直至遇到一個值比x大或相等的數據元素為止,則此數據元素所處的位置就是x待插入的位置。方法二:從順序表的表尾開始依次往前將數據元素值與x進行比較,當數據元素值比x的值大時,則繼續往前進行比較,直至遇到一個值比x小或相等的數據元素為止,則此數據元素所處的位置的后面一個位置就是x待插入的位置。當待插入的位置確定后,則要進行數據元素的移動,由于數據元素的移動都是從表尾元素開始的,因而采用方法二時,可以在確定待插入位置的同時一邊進行比較,一邊進行移動,這樣可以簡化算法的描述形式并提高算法效率。
【算法2-10】例2-4中方法一的設計算法
Status SqListInsert_1(SqList&L,ElemType x)
{ int i; ElemType * newbase;
if(L.length>=L.listsize) //若當前順序表分配空間滿,則追加分配
{ newbase=(ElemType*)realloc(L.elem,(L.listsize+LISTINCREMENT)*sizeof(ElemType));
if(! newbase) //如果空間分配失敗
exit(OVERFLOW);
L.elem=newbase; //修改增加空間后的基址
L.l istsize+=LISTINCREMENT; //修改增加空間后的存儲空間容量
}
for(i=0;i<L.length&&L.elem[i]<x;i++);//確定插入位置
for(int j=L.length-1;j>=i;j--) //插入位置i及其之后的所有元素后移一位
L.elem[j+1]=L.elem[j];
L.elem[i]=x; //插入x
L.length++; //表長加 1
return OK;
}//算法2-1 0 結束
【算法2-11】例2-4中方法二的設計算法
Status SqListInsert_2(SqList&L,ElemType x)
{int i; ElemType *newbase;
if(L.length>=L.listsize)//若當前順序表分配空間滿,則追加分配
{ newbase=(ElemType*)realloc(L.elem,(L.l istsize+LISTINCREMENT)*sizeof(ElemType));
if(! newbase) //如果空間分配失敗
exit(OVERFLOW);
L.elem=newbase; //修改增加空間后的基址
L.l istsize+=LISTINCREMENT;//修改增加空間后的存儲空間容量
}
for(i=L.length-1;i>=0&&L.elem[i]>x;i--)
L.elem[i+1]=L.elem[i]; //一邊比較,一邊進行后移
L.elem[i+1]=x; //插入x到第i+1個位置上
L.length++; //表長加 1
return OK;
}//算法2-1 1 結束
這兩種算法的時間復雜度雖然都為O(n)(n為順序表的表長),但算法2-10中有兩個并列的for循環語句,而算法2-11中只有一個for循環語句,顯然,后者運行時的時間開銷更少。
【例2-5】已知一個順序表L,設計一個算法刪除L中數據元素值為x的所有元素,并使此操作的時間復雜度為O(n),空間復雜度為O(1),其中n為順序表的長度。
【分析】本題涉及的知識點是順序表的刪除操作。如果這題沒有時間復雜度限制的話,很容易想到下面這種方法:從順序表的表頭開始依次對每個數據元素進行掃描,如果遇到值為x的數據元素則將其刪除,直到所有的數據元素都處理完為止。由于在順序表中刪除一個數據元素的時間復雜度為O(n),所以要對n個數據元素進行處理,時間復雜度為O(n2),所以這種設計思想是不符合題目要求的。下面介紹符合題目要求的一種設計思想:
先引進一個計數變量k,用來記錄順序表中值不等于x的數據元素的個數,初始值為0,然后從順序表的表頭開始依次對每個數據元素進行掃描,邊掃描邊統計,當統計到第k個值不等于x的數據元素時,則將其放置到第k個存儲位置中,最后將順序表的長度修改為k即可。
【算法2-12】例2-5的設計算法
Status SqListdel_x(SqList&L,ElemType x)
//刪除當前順序表中所有值為x的數據元素
{int k=0; //用k記錄值不等于x的數據元素的個數
for(int i=0;i<L.length;i++)
{ if(L.elem[i]!=x)
//將第k個值不等于x的數據元素放置到第k個存儲位置中,然后k值加 1
{ L.elem[k++]=L.elem[i];
}
}
L.length=k; //修改順序表的長度為k
}//算法2-12 結束
從此算法的結構本身就可以知道它的時間復雜度為O(n),空間復雜度為O(1)。
- Learning Single:page Web Application Development
- Developing Middleware in Java EE 8
- PHP 編程從入門到實踐
- 零基礎學Java(第4版)
- Learning Network Forensics
- Spring快速入門
- 微服務從小白到專家:Spring Cloud和Kubernetes實戰
- Android Wear Projects
- RealSenseTM互動開發實戰
- Python 3.7從入門到精通(視頻教學版)
- 零基礎學C語言程序設計
- Troubleshooting Citrix XenApp?
- TypeScript 2.x By Example
- TypeScript全棧開發
- 3D Printing Designs:Octopus Pencil Holder